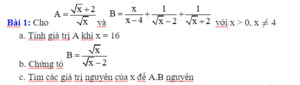a, \(A=\dfrac{\sqrt{x}+2}{\sqrt{x}}=\dfrac{\sqrt{16}+2}{\sqrt{16}}=\dfrac{4+2}{4}=\dfrac{6}{4}=\dfrac{3}{2}\)
b, \(B=\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\)
\(\Rightarrow B=\dfrac{x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(\Rightarrow B=\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(\Rightarrow B=\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(\Rightarrow B=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(\Rightarrow B=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
c,\(AB=\dfrac{\sqrt{x}+2}{\sqrt{x}}.\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
\(\Rightarrow AB=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\)
\(\Rightarrow AB=\dfrac{\sqrt{x}-2+4}{\sqrt{x}-2}\)
\(\Rightarrow AB=1+\dfrac{4}{\sqrt{x}-2}\)
Để AB nguyên thì \(\dfrac{4}{\sqrt{x}-2}\in Z\Rightarrow\sqrt{x}-2\inƯ\left(4\right)\)
Ta có bảng:
| \(\sqrt{x}-2\) | -4 | -2 | -1 | 1 | 2 | 4 |
| x | vô lí | 0 (ktm) | 1 | 9 | 16 | 36 |
Vậy \(x\in\left\{1;9;16;36\right\}\)
a, B=xx−4+1√x−2+1√x+2B=xx−4+1x−2+1x+2
⇒B=x+√x+2+√x−2(√x−2)(√x+2)⇒B=x+x+2+x−2(x−2)(x+2)
⇒B=√x(√x+2)(√x−2)(√x+2)⇒B=x(x+2)(x−2)(x+2)
AB=√x+2√x.√x√x−2AB=x+2x.xx−2
⇒AB=√x−2+4√x−2⇒AB=x−2+4x−2
4√x−2∈Z⇒√x−2∈Ư(4)4x−2∈Z⇒x−2∈Ư(4)
Ta có bảng:
| √x−2x−2 | -4 | -2 | -1 | 1 | 2 | 4 |
| x | vô lí | 0 (ktm) | 1 | 9 | 16 | 36 |
Vậy x∈{1;9;16;36}