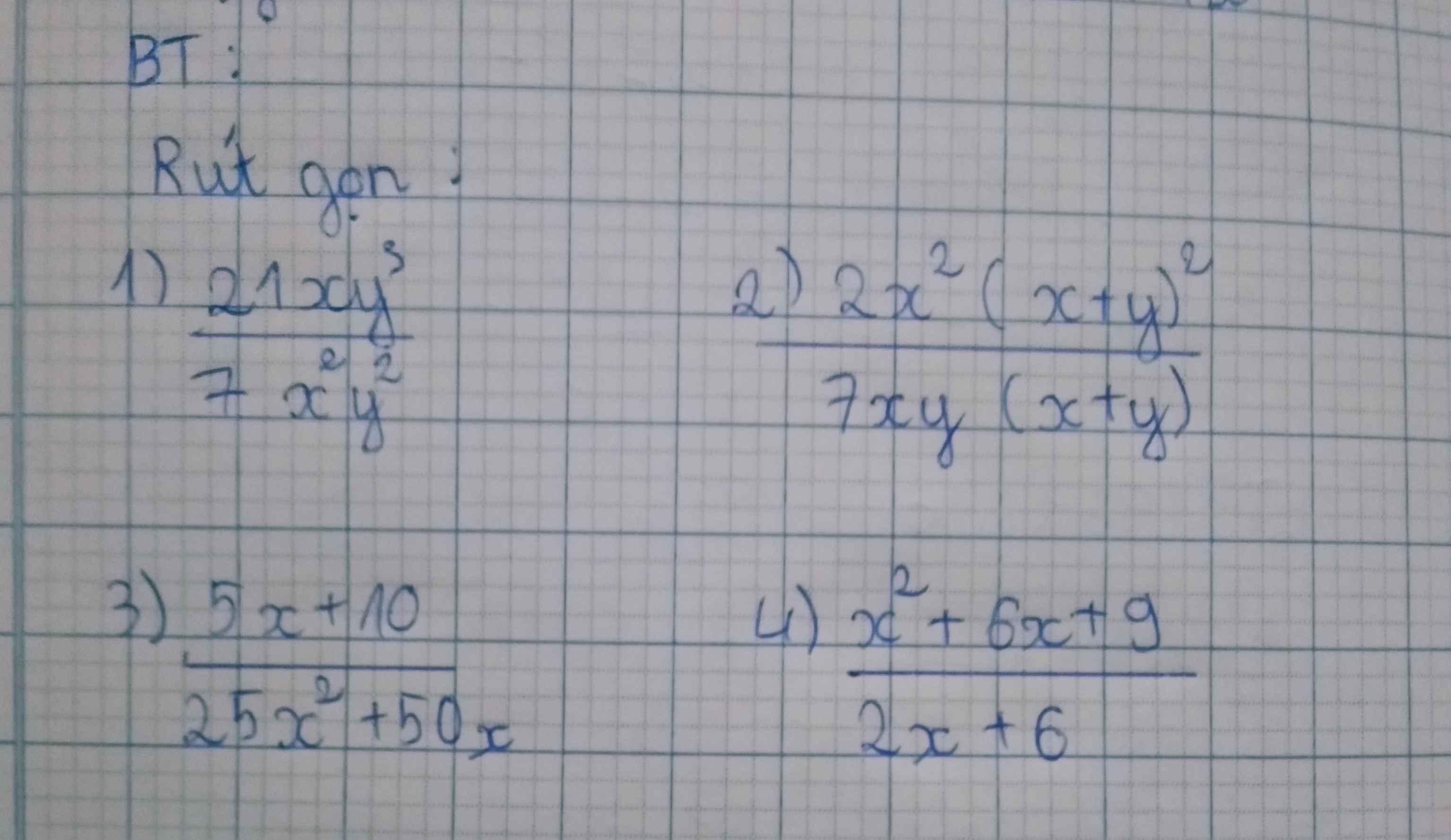Bài 2: Tính chất cơ bản của phân thức

\(=\dfrac{m\left(2m-n\right)}{n\left(2m-n\right)}=\dfrac{m}{n}\)

1: \(=\dfrac{7xy^2\cdot3y}{7xy^2\cdot x}=\dfrac{3y}{x}\)

2: \(=\dfrac{2x^2\left(x+y\right)^2}{7xy\left(x+y\right)}=\dfrac{2x\left(x+y\right)}{7y}\)

3: \(=\dfrac{5\left(x+2\right)}{25x\left(x+2\right)}=\dfrac{1}{5x}\)

4: \(=\dfrac{\left(x+3\right)^2}{2\left(x+3\right)}=\dfrac{x+3}{2}\)

Lời giải:
$\frac{a+b}{a-c}=\frac{a+c}{a-c}$

$\Rightarrow a+b=a+c$

$\Rightarrow b=c$ (đpcm)

\(a,\dfrac{2}{\left(x+1\right)\left(x-3\right)}\\ đk\left\{{}\begin{matrix}x+1\ne0\\x-3\ne\end{matrix}\right.=>\left\{{}\begin{matrix}x\ne-1\\x\ne3\end{matrix}\right.\)

\(d,\dfrac{2x+1}{x^2-5x+6}=\dfrac{2x+1}{\left(x-2\right)\left(x-3\right)}\\ đk\left\{{}\begin{matrix}x-2\ne0\\x-3\ne0\end{matrix}\right.=>x\ne2;x\ne3\)

\(c,x^2\ge0\forall x\\ y^2\ge0\forall y\)

=> \(x\ne0;y\ne0\)

\(d,\dfrac{5x+y}{x^2+6x+10}\\ đkx^2+6x+10\ne0\)

đề bài là gì em nhỉ 

(x-3y)²-(x-3y)
`= [  x^2 - 2 . 3y . x + (3y)^2 ] -(x-3y) `
` = x^2 -6xy + 9y^2 - x + 3y `

x(x+y)²+xy(x+y)

`=x(x^2 + 2xy + y^2) + x^2y + xy^2` 

` = x^3 + 2x^2y + xy^2 + x^2y + xy^2` 

` = x^3 + 3x^2y + 2xy^2` 

`a, (x-3y)^2 - (x-3y) = (x-3y)(x-3y-1)`

`= x^2 - 3xy - 3xy + 9y^2 - x + 3y`

`= x^2 - 6xy + 3y - x + 9y^2`

`b, x(x+y)^2 + xy(x+y)`

`= (x+y)(x^2+2xy)`

`= (x^3 + x^2y + 2x^2y + 2xy^2)`

`4x^2-4=0`

`<=>4(x^2-1)=0`

`<=>x^2-1=0`

`<=>x^2=1`

`<=>x=+-1`

Vậy `S={+-1}`

\(\Leftrightarrow4x^2=4\) 

\(\Leftrightarrow4x^2=2^2\) 

\(\Leftrightarrow4x=\pm2\)  

\(\Rightarrow\left[{}\begin{matrix}4x=2\\4x=-2\end{matrix}\right.\) 

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-\dfrac{1}{2}\end{matrix}\right.\)

Vậy. .

4x^2-4=0

<=>4x^2=4

<=>x^2=4/4

<=>x^2=1

<=>x=căn 1÷1

Thời gian người đó đi nửa quãng đường đầu là:

`15:15=1(giờ)`

Thời gian người đó đi nửa quãng đường sau:

`15:10=1,5(giờ)`

Tổng thời gian người đó đi quãng đường `AB` là:

`1+1,5=2,5(giờ)`

Vận tốc trung bình của người đó đi trên cả quãng đường `AB` là:

`30:2,5=12(km//h)`

Xét ΔABC có AD là phân giác

nên BD/AB=CD/AC

=>CD/8,5=3/5

hay CD=5,1(cm)

=>BC=13,6(cm)

Ta có :

AD là đường phân giác của \(\widehat{BAC}\)

=> \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)

=> \(\dfrac{5}{8,5}=\dfrac{3}{CD}\)

=> CD = 5,1 (cm)

Ta có : BC = BD + CD

=> BD = 3 + 5,1

=> BD = 8,1 (cm)