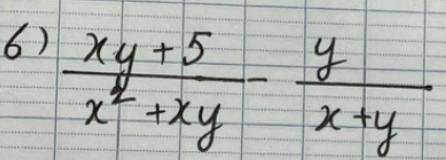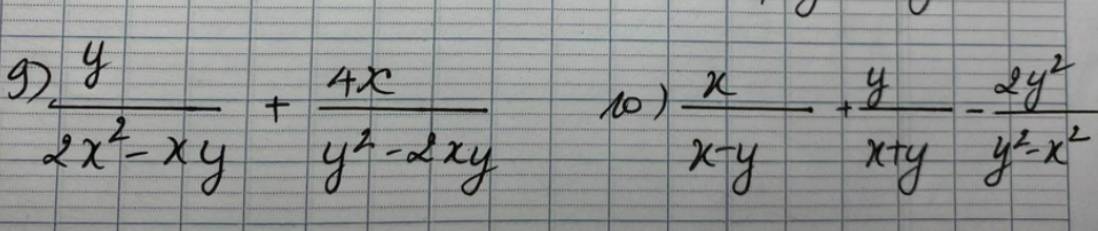6) \(\dfrac{xy+5}{x^2+xy}-\dfrac{y}{x+y}\)
\(=\dfrac{xy+5}{x\left(x+y\right)}-\dfrac{xy}{x\left(x+y\right)}\)
\(=\dfrac{xy+5-xy}{x\left(x+y\right)}\)
\(=\dfrac{5}{x\left(x+y\right)}\)
\(=\dfrac{5}{x^2+xy}\)
9) \(\dfrac{y}{2x^2-xy}+\dfrac{4x}{y^2-2xy}\)
\(=\dfrac{y}{x\left(2x-y\right)}+\dfrac{4x}{y\left(y-2x\right)}\)
\(=\dfrac{y^2}{xy\left(2x-y\right)}-\dfrac{4x^2}{xy\left(2x-y\right)}\)
\(=-\dfrac{4x^2-y^2}{xy\left(2x-y\right)}\)
\(=-\dfrac{\left(2x-y\right)\left(2x+y\right)}{xy\left(2x-y\right)}\)
\(=-\dfrac{2x+y}{xy}\)
10) \(\dfrac{x}{x-y}+\dfrac{y}{x+y}-\dfrac{2y^2}{y^2-x^2}\)
\(=\dfrac{x\left(x+y\right)}{\left(x+y\right)\left(x-y\right)}+\dfrac{y\left(x-y\right)}{\left(x+y\right)\left(x-y\right)}+\dfrac{2y^2}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{x^2+xy+xy-y^2+2y^2}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{x^2+2xy+y^2}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{\left(x+y\right)^2}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{x+y}{x-y}\)