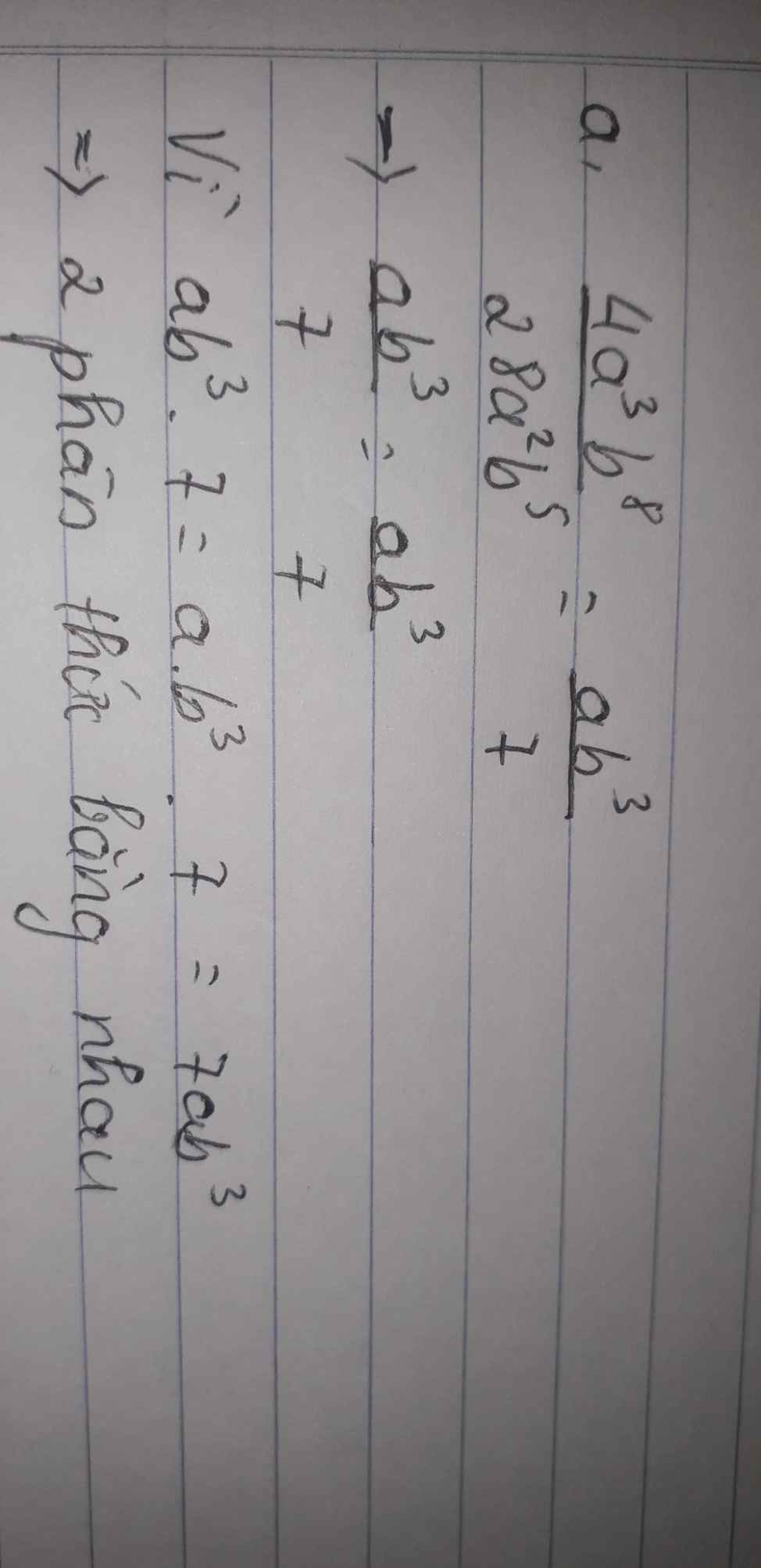
Bài 2: Tính chất cơ bản của phân thức
Dùng tính chất cơ bản của phân thức, hãy giải thích vì sao?
\(\dfrac{3-2x}{2x-3y}=\dfrac{2x-3}{3y-2x}\)
Ta có \(\left\{{}\begin{matrix}\left(3-2x\right)\left(3y-2x\right)\\\left(2x-3y\right)\left(2x-3\right)\end{matrix}\right.\left\{{}\begin{matrix}9y-6x-6xy+4x^2\\4x^2-6y-6xy+9y\end{matrix}\right.\\ =>\dfrac{3-2x}{2x-3y}=\dfrac{2x-3}{3y-2x}\)
Đúng 2
Bình luận (0)
\(\dfrac{(x+1)^2}{x^2+x}=\dfrac{(x+1)^2}{x(x+1)}=\dfrac{x+1}{x}\)
Đúng 1
Bình luận (0)
\(\dfrac{x^2-xy}{6y^2-6xy}\)=
\(\dfrac{x^2-xy}{6y^2-6xy}=\dfrac{x\left(x-y\right)}{-6y\left(x-y\right)}=-\dfrac{x}{6y}\)
Đúng 1
Bình luận (0)
Đọc tiếp
Lời giải:
a.
\(\frac{-4xy^2}{2x^4y}=\frac{2xy.(-2y)}{2xy.x^3}=\frac{-2y}{x^3}=\frac{2y}{-x^3}\)
b.
\(\frac{m^2-2mn+n^2}{m^2-n^2}=\frac{(m-n)^2}{(m-n)(m+n)}=\frac{m-n}{m+n}\)
c.
\(\frac{3a(a-b)^2}{33a^2-33ab}=\frac{3a(a-b)^2}{33a(a-b)}=\frac{3(a-b)}{33}=\frac{a-b}{11}\)
d.
\(\frac{a^2+4ab+4b^2}{a^2-4b^2}=\frac{(a+2b)^2}{(a-2b)(a+2b)}=\frac{a+2b}{a-2b}\)
Đúng 0
Bình luận (0)
Đọc tiếp
Đọc tiếp
\(\left(a-\dfrac{4}{3}\right)^2+\left(b-\dfrac{4}{3}\right)^2+\left(c-\dfrac{4}{3}\right)^2\\ =a^2+b^2+c^2-\dfrac{8}{3}\left(a+b+c\right)+\dfrac{16}{9}\cdot3\\ =a^2+b^2+c^2-\dfrac{8}{3}\cdot2+\dfrac{16}{3}\\ =a^2+b^2+c^2-\dfrac{16}{3}+\dfrac{16}{3}=a^2+b^2+c^2\)
Lại có \(a+b+c=2\Leftrightarrow\left(a+b+c\right)^2=4\)
\(\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)=4\\ \Leftrightarrow a^2+b^2+c^2=4-2\left(ab+bc+ca\right)=2\left[2-\left(ab+bc+ca\right)\right]\\ \Leftrightarrow\dfrac{a^2+b^2+c^2}{2}=2-\left(ab+bc+ca\right)\)
Thay vào \(P\Leftrightarrow P=\dfrac{\dfrac{a^2+b^2+c^2}{2}}{a^2+b^2+c^2}=\dfrac{1}{2}\)
Đúng 2
Bình luận (4)
Đọc tiếp
\(xyz=1\Leftrightarrow\left\{{}\begin{matrix}xy=\dfrac{1}{z}\\yz=\dfrac{1}{x}\\xz=\dfrac{1}{y}\end{matrix}\right.\)
\(\left(x+\dfrac{1}{x}\right)\left(y+\dfrac{1}{y}\right)\left(z+\dfrac{1}{z}\right)\\ =\left(xy+\dfrac{x}{y}+\dfrac{y}{x}+\dfrac{1}{xy}\right)\left(z+\dfrac{1}{z}\right)\\ =xyz+\dfrac{xy}{z}+\dfrac{xz}{y}+\dfrac{yz}{x}+\dfrac{x}{yz}+\dfrac{y}{xz}+\dfrac{z}{xy}+\dfrac{1}{xyz}\\ =2+\dfrac{1}{z^2}+\dfrac{1}{y^2}+\dfrac{1}{x^2}+x^2+y^2+z^2\)
\(\Leftrightarrow P=x^2+y^2+z^2+\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+8-2-\dfrac{1}{x^2}-\dfrac{1}{y^2}-\dfrac{1}{z^2}-x^2-y^2-z^2\\ \Leftrightarrow P=6\)
Đúng 1
Bình luận (1)