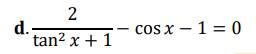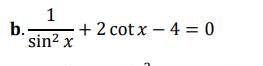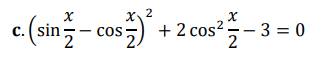
Bài 2: Phương trình lượng giác cơ bản

\(\Leftrightarrow1-2\cdot sin\left(\dfrac{x}{2}\right)\cdot cos\left(\dfrac{x}{2}\right)+2\cdot cos^2\left(\dfrac{x}{2}\right)-3=0\)

\(\Leftrightarrow1-sinx+2\cdot\dfrac{1+cosx}{2}-3=0\)

\(\Leftrightarrow1-sinx+1+cosx-3=0\)

\(\Leftrightarrow-sinx+cosx-1=0\)

\(\Leftrightarrow sinx-cosx+1=0\)

\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{pi}{4}\right)=-1\)

\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{pi}{4}=-\dfrac{pi}{4}+k2pi\\x-\dfrac{pi}{4}=\dfrac{5}{4}pi+k2pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=k2pi\\x=\dfrac{3}{2}pi+k2pi\end{matrix}\right.\)

ĐKXĐ: x<>pi/2+kpi

\(\Leftrightarrow2:\left(\dfrac{sin^2x}{cos^2x}+1\right)-cosx-1=0\)

\(\Leftrightarrow2:\left(\dfrac{1-cos^2x+cos^2x}{cos^2x}\right)-cosx-1=0\)

\(\Leftrightarrow2cos^2x-cosx-1=0\)
\(\Leftrightarrow\left(cosx-1\right)\left(2cosx+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=k2pi\\x=\pm\dfrac{2}{3}pi+k2pi\end{matrix}\right.\)

\(\Leftrightarrow1+cot^2x+2cotx-4=0\)

=>\(cot^2x+2cotx-3=0\)

=>(cotx+3)(cotx-1)=0

=>x=pi/4+kpi hoặc x=arccot(-3)+kpi

a.

\(\Leftrightarrow sin2x+cos2x+\dfrac{1-cos2x}{2}+1=0\)

\(\Leftrightarrow2sin2x+cos2x=3\)

Do \(2^2+1^2< 3^2\) nên pt đã cho vô nghiệm theo điều kiện có nghiệm của pt lượng giác bậc nhất

f.

\(\Leftrightarrow3cos^24x+3sin^24x+2sin^24x=2-2\sqrt{3}sin4x.cos4x\)

\(\Leftrightarrow3+1-cos8x=2-\sqrt{3}sin8x\)

\(\Leftrightarrow\sqrt{3}sin8x-cos8x=-2\)

\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sin8x-\dfrac{1}{2}cos8x=-1\)

\(\Leftrightarrow sin\left(8x-\dfrac{\pi}{6}\right)=-1\)

\(\Leftrightarrow8x-\dfrac{\pi}{6}=-\dfrac{\pi}{2}+k2\pi\)

\(\Leftrightarrow...\)

Câu 2:

a: ĐKXĐ: \(2x-\dfrac{pi}{3}< >\dfrac{pi}{2}+kpi\)

=>\(x< >\dfrac{5}{12}pi+\dfrac{kpi}{2}\)

\(PT\Leftrightarrow2x-\dfrac{pi}{3}=\dfrac{pi}{6}+kpi\)

=>2x=pi/2+kpi

=>x=pi/4+kpi/2

b: \(\Leftrightarrow\left[{}\begin{matrix}45^0-x=45^0+k\cdot360^0\\45^0-x=135^0+k\cdot360^0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-k\cdot360^0\\x=-90^0-k\cdot360^0\end{matrix}\right.\)

c: \(\Leftrightarrow sin3x=sin\left(-x\right)\)

=>3x=-x+k2pi hoặc 3x=pi+x+k2pi

=>4x=k2pi hoặc 2x=pi+k2pi

=>x=kpi/2 hoặc x=pi/2+kpi

`cos^3 x.cos 2x-cos^2 x=0`

`<=>cos^2 x(cos x.cos 2x-1)=0`

`<=>cos x[cos x(2cos^2 x-1)-1]=0`

`<=>cos x(2cos^3 x-cos x-1)=0`

`<=>[(cos x=0),(cos x=1):}`

`<=>[(x=\pi/2+k\pi),(x=k2\pi):}`       `(k in ZZ)`

Đề là:\(cos^3x . cos2x - cos^2x = 0\) à bạn?

a: =>sin2x=-1/2

=>\(\left[{}\begin{matrix}2x=-\dfrac{pi}{6}+k2pi\\2x=\dfrac{7}{6}pi+2kpi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{pi}{12}+kpi\\x=\dfrac{7}{12}pi+kpi\end{matrix}\right.\)

mà 0<x<pi

nên \(x\in\left\{\dfrac{11}{12}ơi;\dfrac{7}{12}pi\right\}\)

b: \(\Leftrightarrow x-5=\dfrac{pi}{6}+kpi\)

=>x=pi/6+kpi+5

mà -pi<x<pi

nên \(x\in\left\{\dfrac{pi}{6}+5\right\}\)

a.

Do \(-1\le sin3x\le1\Rightarrow-4\le sin3x-3\le-2\)

\(y_{max}=-2\) khi \(sin3x=1\)

\(y_{min}=-4\) khi \(sin3x=-1\)

b.

Do \(-1\le cos2x\le1\Rightarrow0\le cos2x+1\le2\)

\(y_{max}=2\) khi \(cos2x=1\)

\(y_{min}=0\) khi \(cos2x=-1\)

c.

\(y=sin2x.cos2x+2=\dfrac{1}{2}sin4x+2\)

Do \(-1\le sin4x\le1\Rightarrow\dfrac{3}{2}\le\dfrac{1}{2}sin4x+2\le\dfrac{5}{2}\)

\(y_{max}=\dfrac{5}{2}\) khi \(sin4x=1\)

\(y_{max}=\dfrac{3}{2}\) khi \(sin4x=-1\)

Giúp em với ạ