Tìm công thức của số hạng tổng quát của dãy biết:
\(\left\{{}\begin{matrix}u_{n+1}=\sqrt{u_n+1}\\u_1=1\end{matrix}\right.\)
Tìm công thức của số hạng tổng quát của dãy biết:
\(\left\{{}\begin{matrix}u_{n+1}=\sqrt{u_n+1}\\u_1=1\end{matrix}\right.\)
Xét tính tăng giảm của dãy số (-1) mũ n × (2n -5)
A=\(u_{n+1}-u_n=\left(2n+2-5\right)\cdot\left(-1\right)^{n+1}-\left(2n-5\right)\cdot\left(-1\right)^n\)
\(=\left(2n-3\right)\cdot\left(-1\right)^{n+1}-\left(2n-5\right)\cdot\left(-1\right)^n\)
TH1:n là số chẵn
=>A=-(2n-3)-(2n-5)=-2n+3-2n+5=-4n+8
\(u_{n+1}-u_n=-4\left(n+1\right)+8+4n-8=-4n-4+4n=-4< 0\)
=>Dãy số giảm
TH2: n là số lẻ
A=(2n-3)-(2n-5)*(-1)
=2n-3+2n-5=4n-8
\(u_{n+1}-u_n=4\left(n+1\right)-8-4n+8=4>0\)
=>Dãy số tăng
Cho dãy số un có số hạng tổng quát \(u_n=\dfrac{n^2+n+1}{n^2+n}\). Đặt \(S=u_1+u_2+u_3+....+u_{2023}=\dfrac{a}{b}\) với a,b là các số nguyên dương và phân số \(\dfrac{a}{b}\) tối giản. Tính \(a-b^2\)
A=\(\dfrac{u_{n+1}}{u_n}=\dfrac{n+1}{3^{n+1}}:\dfrac{n}{3^n}=\dfrac{n+1}{n}\cdot\dfrac{1}{3}=\dfrac{n+1}{3n}=\dfrac{1}{3}+\dfrac{1}{3n}< =\dfrac{2}{3}\)
=>(un)<=2/3 với mọi n
cho dãy số 2,5,8,11,...,302
1. số 100 có thuộc dãy số trên ko ?
2.hỏi số hạng 113 là số thứ bao nhiêu ?
nhờ các bạn giúp mình gấp một chút ah
Dãy số trên có dạng: \(\left\{{}\begin{matrix}u_n=3n-1\\n\ge1\end{matrix}\right.\)
\(3n-1=100\Rightarrow n=\dfrac{101}{3}\notin N\Rightarrow100\) ko thuộc dãy trên
Số hạng thứ 113 là: \(3.113-1=338\)
Lời giải:
1. Các số trong dãy đều là số chia 3 dư 2.
100 chia 3 dư 1 nên không thuộc dãy trên
2.
Số thứ nhất: $2=3.1-1$
Số thứ hai: $5=3.2-1$
Số thứ ba: $8=3.3-1$
.....
Số 113 là số hạng thứ x thì: $113=3.x-1$
$\Rightarrow x=38$
Vậy số 113 là số thứ 38.
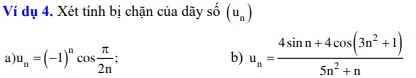
giải hộ mình câu b với ạ
Cho dãy số (un):
\(\left\{{}\begin{matrix}u_1=3\\u_{n+1}=\dfrac{u_n^2+2007u_n+2}{2010}\end{matrix}\right.\) Với n lớn hơn hoặc bằng 1
Tính
\(\lim\limits_{n\rightarrow\infty}\left(\dfrac{u_1-1}{u_2-2}+\dfrac{u_2-1}{u_3-2}+...+\dfrac{u_n-1}{u_{n+1}-2}\right)\)
Dễ dàng quy nạp mọi số hạng của dãy đã cho đều \(\ge3\)
(Do \(u_k\ge3\Rightarrow u_{k+1}=\dfrac{u_k^2+2007u_k+2}{2010}\ge\dfrac{9+3.2007+2}{2010}>3\))
Từ đó: \(u_{n+1}=\dfrac{\left(u_n+2007\right)u_n+2}{2010}\ge\dfrac{2010u_n+2}{2010}=u_n+\dfrac{1}{505}\)
\(\Rightarrow u_{n+1}\ge u_1+n.\dfrac{1}{505}\)
Mà \(\lim\left(\dfrac{n}{505}+3\right)=\infty\Rightarrow\lim\left(u_{n+1}\right)=\infty\)
\(\Rightarrow\lim\dfrac{1}{u_{n+1}-2}=0\)
Từ giả thiết suy ra:
\(u_{n+1}-2=\dfrac{\left(u_n-2\right)\left(u_n+2009\right)}{2010}\)
\(\Rightarrow\dfrac{u_n+2009}{u_{n+1}-2}=\dfrac{2010}{u_n-2}\)
\(\Rightarrow\dfrac{u_n-1+2010}{u_{n+1}-2}=\dfrac{2010}{u_n-2}\)
\(\Rightarrow\dfrac{u_n-1}{u_{n+1}-2}=\dfrac{2010}{u_n-2}-\dfrac{2010}{u_{n+1}-2}\)
\(\Rightarrow S=2010\left(\dfrac{1}{u_1-2}-\dfrac{1}{u_2-2}+\dfrac{1}{u_2-2}-\dfrac{1}{u_3-2}+...-\dfrac{1}{u_{n+1}-2}\right)\)
\(\Rightarrow S=2010\left(\dfrac{1}{u_1-2}-\dfrac{1}{u_{n+1}-2}\right)=2010\left(1-\dfrac{1}{u_{n+1}-2}\right)\)
\(\Rightarrow\lim\left(S\right)=2010\)
Dễ dàng CM được theo qui nạp ta có $u_n > 2$ $\forall n\ge 1$
Xét hiệu $u_{n+1} - u_n = \dfrac{u_n^2-3u_n+2}{2010} = \dfrac{(u_n-1)(u_n-2)}{2010}$
Dễ thấy với $u_n > 2$ thì $\dfrac{(u_n-1)(u_n-2)}{2010} > 0$ nên $u_{n+1} > u_n$
Suy ra dãy $u_n$ tăng ngặt.
Giả sử dãy bị chặn trên. Theo định lý weierstrass thì dãy đã cho có giới hạn.
Đặt $\lim u_n = a(a>2)$. Giải PT giới hạn ta được $a = 1$ or $a=2$ . Hai trường hợp đều không thỏa suy ra $\lim u_n = +\infty$
Từ HTTH ta suy ra:
$2010u_{n+1} = u_n^2+2007u_n+2$
$\to 2010(u_{n+1}-2) = (u_n-2)(u_n+2009)$
Đến đây bạn làm như thầy Lâm là được
Vậy $\displaystyle\lim_{n \to \infty} \displaystyle\sum_{k=1}^n \dfrac{u_k-1}{u_{k+1}-2} = \dfrac{2010}{u_1-2} = 2010$
giả sử ptr ax^2+bx+c=0 (a khác 0) có 2 nghiệm phana biệt m,p ( m<p ) xét dãy số {Xn} với n= 0,1,2,... được xác định bởi số x0 cho trước và điều kiện Xn(aXn-1+b)+c=0 với n =1,2,...
tính LImXn
help với ạ
Cho dãy an xác định bởi công thức
\(\left\{{}\begin{matrix}a_1=6,a_2=0\\n.a_{n+2}=\left(2n+1\right)a_{n+1}-\left(n+1\right)a_n+3n^2+3n\end{matrix}\right.\) n= 1,2,3..
Tìm SHTQ
\(\Leftrightarrow n\left(a_{n+2}-a_{n+1}\right)=\left(n+1\right)\left(a_{n+1}-a_n\right)+3n\left(n+1\right)\)
\(\Leftrightarrow\dfrac{a_{n+2}-a_{n+1}}{n+1}=\dfrac{a_{n+1}-a_n}{n}+3\)
Đặt \(\dfrac{a_{n+1}-a_n}{n}=b_n\Rightarrow\left\{{}\begin{matrix}b_1=\dfrac{a_2-a_1}{1}=-6\\b_{n+1}=b_n+3\end{matrix}\right.\)
\(\Rightarrow b_n\) là cấp số cộng với công sai 3
\(\Rightarrow b_n=b_1+\left(n-1\right)d=-6+3\left(n-1\right)=3n-9\)
\(\Rightarrow a_{n+1}-a_n=n\left(3n-9\right)=3n^2-9n\)
\(\Rightarrow a_{n+1}-\left(n+1\right)^3+6\left(n+1\right)^2-5\left(n+1\right)=a_n-n^3+6n^2-5n\)
Đặt \(a_n-n^3+6n^2-5n=c_n\Rightarrow\left\{{}\begin{matrix}c_1=6-1+6-5=6\\c_{n+1}=c_n=...=c_1=6\end{matrix}\right.\)
\(\Rightarrow a_n=n^3-6n^2+5n+6\)
1.
\(\lim\left(u_n-2\right)=0\Rightarrow\lim\left(u_n\right)=2\)
2.
\(\lim\left(n+2\right)=+\infty\)
3.
\(\lim\left(u_n+v_n\right)=\lim\left(u_n\right)+\lim\left(v_n\right)=4+2=6\)
4.
\(\lim\dfrac{1}{n+3}=\dfrac{1}{+\infty}=0\)
5.
\(\lim2^n=+\infty\)
6.
\(\lim\left(u_n.v_n\right)=\lim u_n.\lim v_n=2.3=6\)
7.
\(\lim\left(u_n-2\right)=\lim\left(u_n\right)-\lim2=5-2=3\)
8.
\(\lim\limits_{x\rightarrow1}\left[f\left(x\right)+g\left(x\right)\right]=\lim\limits_{x\rightarrow1}f\left(x\right)+\lim\limits_{x\rightarrow1}g\left(x\right)=3+2=5\)
9.
\(\lim\limits_{x\rightarrow1}f\left(x\right)=2\)
10.
\(\lim\limits_{x\rightarrow1}\left(2x+1\right)=2.1+1=3\)