Bài 2: Dãy số

\(u_n=\dfrac{1}{n+1}\Rightarrow u_{n+1}=\dfrac{1}{n+2}\)

\(\Rightarrow u_n-u_{n+1}=\dfrac{1}{n+1}-\dfrac{1}{n+2}=\dfrac{1}{\left(n+1\right)\left(n+2\right)}>0\)

\(\Rightarrow u_{n+1}< u_n\Rightarrow\) dãy giảm

Do \(\dfrac{1}{n+1}>0\Rightarrow\) dãy bị chặn dưới bởi 0

\(u_n-1=\dfrac{1}{n+1}-1=-\dfrac{n}{n+1}< 0\Rightarrow u_n< 1\)

\(\Rightarrow\) Dãy bị chặn trên bởi 1

\(\Rightarrow\) Dãy bị chặn

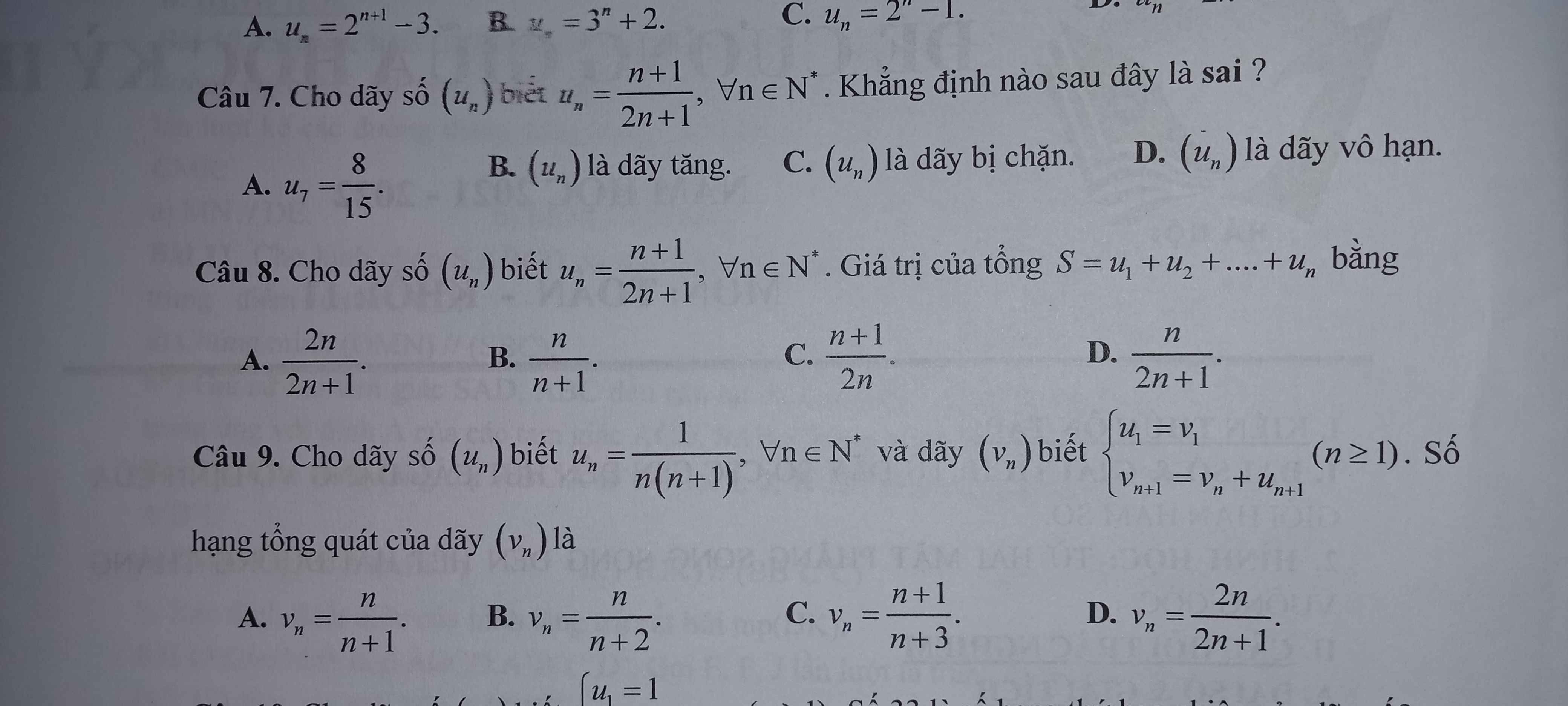
7.

\(u_1=\dfrac{1+1}{2.1+1}=\dfrac{2}{3}\) ; \(u_2=\dfrac{2+1}{2.2+1}=\dfrac{3}{5}\Rightarrow u_1-u_2=\dfrac{2}{3}-\dfrac{3}{5}=\dfrac{1}{15}>0\)

\(\Rightarrow\) Dãy đã cho là dãy giảm nên đáp án B sai

8.

Đề bài sai, rõ ràng \(u_1+u_2>1\) nhưng tất cả công thức trong dãy đều cho tổng nhỏ hơn 1

9.

\(u_{n+1}=\dfrac{1}{\left(n+1\right)\left(n+2\right)}\); \(v_1=u_1=\dfrac{1}{2}\)

\(v_{n+1}=v_n+\dfrac{1}{\left(n+1\right)\left(n+2\right)}=v_n+\dfrac{1}{n+1}-\dfrac{1}{n+2}\)

\(\Rightarrow v_{n+1}+\dfrac{1}{\left(n+1\right)+1}=v_n+\dfrac{1}{n+1}\)

Đặt \(v_n+\dfrac{1}{n+1}=x_n\Rightarrow\left\{{}\begin{matrix}x_1=v_1+\dfrac{1}{2}=1\\x_{n+1}=x_n=...=x_1=1\end{matrix}\right.\)

\(\Rightarrow v_n+\dfrac{1}{n+1}=1\Rightarrow v_n=1-\dfrac{1}{n+1}=\dfrac{n}{n+1}\)

3.

\(u_2=\dfrac{1}{2-u_1}=\dfrac{1}{2-\dfrac{1}{2}}=\dfrac{2}{3}\)

\(u_3=\dfrac{1}{2-u_2}=\dfrac{1}{2-\dfrac{2}{3}}=\dfrac{3}{4}\)

\(u_4=\dfrac{1}{2-\dfrac{3}{4}}=\dfrac{4}{5}\)

4.

\(u_1=\dfrac{2^{1+1}+1}{2^1}=\dfrac{5}{2}\)

\(u_3=\dfrac{2^4+1}{2^3}=\dfrac{17}{8}\)

\(u_5=\dfrac{2^6+1}{2^5}=\dfrac{65}{32}\)

5. Đề bị khuất

Câu 2: Chọn A.

Câu 3: Chọn B.

Câu 4: Chọn C.

Bạn đã yêu cầu Câu 5, hình bị mất một phần câu 5! Bạn kiểm tra giúp mình!

5.

\(\dfrac{2n}{n^2+1}=\dfrac{9}{41}\Rightarrow9n^2+9=82n\)

\(\Rightarrow9n^2-82n+9=0\Rightarrow\left[{}\begin{matrix}n=9\\n=\dfrac{1}{9}\notin Z\left(loại\right)\end{matrix}\right.\)

Vậy đó là số hạng thứ 9

bn tham khảo:

Lời giải: 

ĐK: $x\neq 0$

PT $\Leftrightarrow (1-\frac{1}{x})+(1-\frac{2}{x})+....+(1-\frac{x-1}{x})=3$

$\Leftrightarrow (x-1)-(\frac{1}{x}+\frac{2}{x}+...+\frac{x-1}{x})=3$

$\Leftrightarrow (x-1)-\frac{1+2+...+(x-1)}{x}=3$

$\Leftrightarrow (x-1)-\frac{x(x-1)}{2x}=3$

$\Rightarrow x^2-7x=0$

$\Rightarrow x=7$ (do $x\neq 0$)

Trước hết ta chứng minh \(0< u_n\le1+\sqrt{2}\):

Ta thấy: \(0< u_1=2\le1+\sqrt{2}\)

Giả sử điều này đúng đến \(0< u_k\le1+\sqrt{2}\)

Ta có: \(u_{k+1}=\dfrac{3u_k+1}{u_k+1}>0\)

Lại có: \(u_{k+1}=\dfrac{3u_k+1}{u_k+1}=3-\dfrac{2}{u_k+1}\le3-\dfrac{2}{1+\sqrt{2}}\le3-1=2\le1+\sqrt{2}\)

\(\Rightarrow0< u_{k+1}\le1+\sqrt{2}\)

Theo nguyên lí quy nạp, ta được: \(0< u_n\le1+\sqrt{2}\)

Khi đó ta có:

\(u_{n+1}-u_n=\dfrac{3u_n+1}{u_n+1}-u_{n\text{​​}}\)

\(=\dfrac{3u_n+1-u_n^2-u_n}{u_n+1}\)

\(=\dfrac{-u_n^2+2u_n+1}{u_n+1}\)

\(=-\dfrac{\left(u_n-1-\sqrt{2}\right)\left(u_n-1+\sqrt{2}\right)}{u_n+1}\ge0\)

\(\Rightarrow u_{n+1}\ge u_n\)

\(\Rightarrow\) Dãy tăng.