\(\left(x^2-1\right)\left(x^2-2x\right)=x^4-2x^3-x^2+2x\)
\(\left(x^2-1\right)\left(x^2-2x\right)=x^4-2x^3-x^2+2x\)
\(=x^4-x^3-x^3+x^2-2x^2+2x\)
\(=x^3.\left(x-1\right)-x^2.\left(x-1\right)-2x.\left(x-1\right)\)
\(=\left(x-1\right)\left(x^3-x^2-2x\right)\)
\(=\left(x-1\right).\left(x^3-2x^2+x^2-2x\right)\)
\(=\left(x-1\right).\left[x^2.\left(x-2\right)+x.\left(x-2\right)\right]\)
\(=\left(x-1\right)\left(x-2\right)\left(x^2+x\right)=\left(x-2\right)\left(x-1\right)x\left(x+1\right)\)
Chúc bạn học tốt!!!






 CÁC BẠN GIÚP MÌNH NHÉ MÌNH CẢM ƠN
CÁC BẠN GIÚP MÌNH NHÉ MÌNH CẢM ƠN
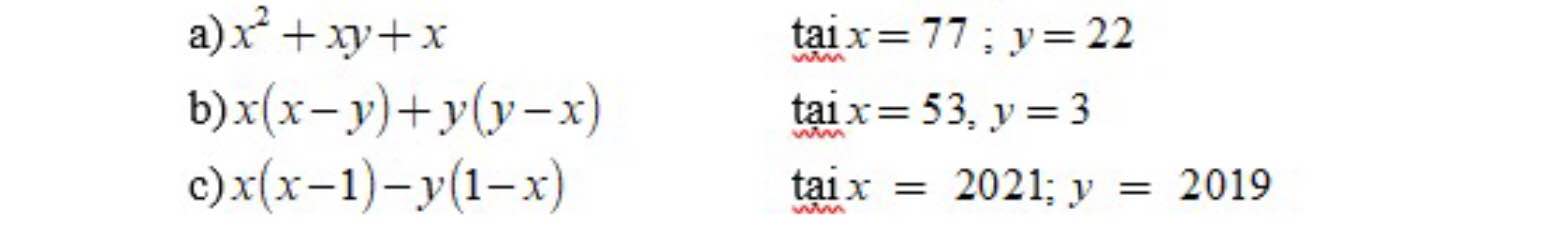 bài này nữa thôi các anh chị :3 em cảm ơn nhiều ạ
bài này nữa thôi các anh chị :3 em cảm ơn nhiều ạ