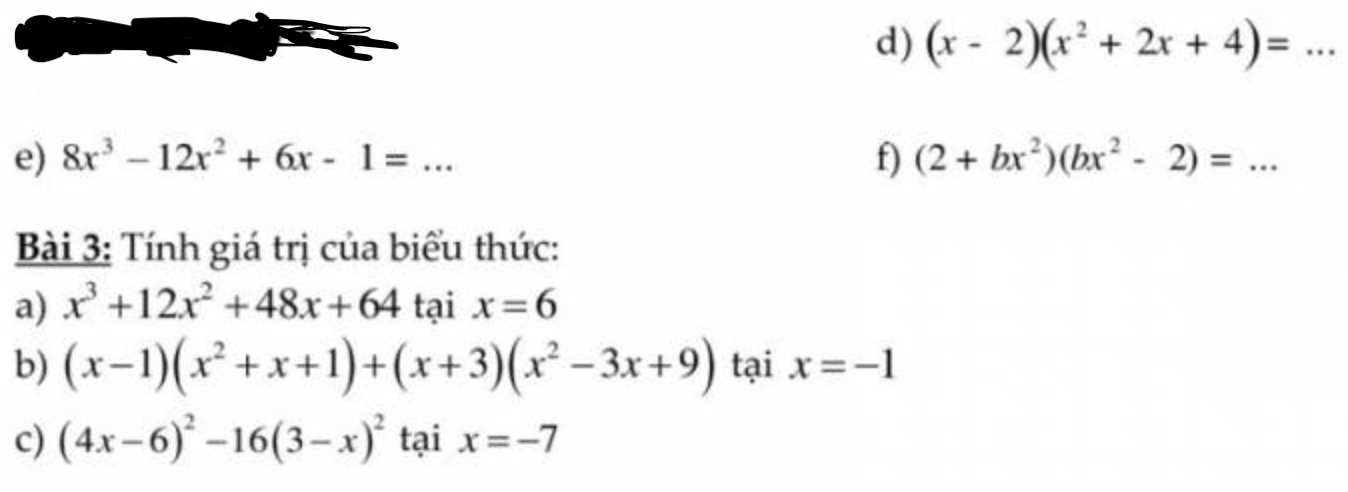b)\(3x\left(x+3y\right)-6xy\left(x+3y\right)\)
\(=\left(3x-6xy\right)\left(x+3y\right)\)
c)\(x\left(x+y\right)-5x-5y\)
\(=x\left(x+y\right)-5\left(x+y\right)\)
\(=\left(x-5\right)\left(x+y\right)\)
Bài 1:
b. \(3x\left(x+3y\right)-6xy\left(x+3y\right)\)
= (3x - 6xy)(x + 3y)
= 3x(1 - 2y)(x + 3y)
c. \(x\left(x+y\right)-5x-5y\)
= x(x + y) - 5(x + y)
= (x - 5)(x + y)
d. \(3\left(x-y\right)-5x\left(y-x\right)\)
= 3(x - y) + 5x(x - y)
= (3 + 5x)(x - y)
Bài 3:
a. x + 6x2 = 0
<=> x(1 + 6x) = 0
<=> \(\left[{}\begin{matrix}x=0\\1+6x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{-1}{6}\end{matrix}\right.\)
b. 2(x + 3) - x(x + 3) = 0
<=> (2 - x)(x + 3) = 0
<=> \(\left[{}\begin{matrix}2-x=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)
c. 5x(x - 2) - (2 - x) = 0
<=> 5x(x - 2) + (x - 2) = 0
<=> (5x + 1)(x - 2) = 0
<=> \(\left[{}\begin{matrix}5x+1=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-1}{5}\\x=2\end{matrix}\right.\)
d. (x + 1) = (x + 1)2
<=> (x + 1) - (x + 1)2 = 0
<=> (1 - x - 1)(x + 1) = 0
<=> -x(x + 1) = 0
<=> \(\left[{}\begin{matrix}-x=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)




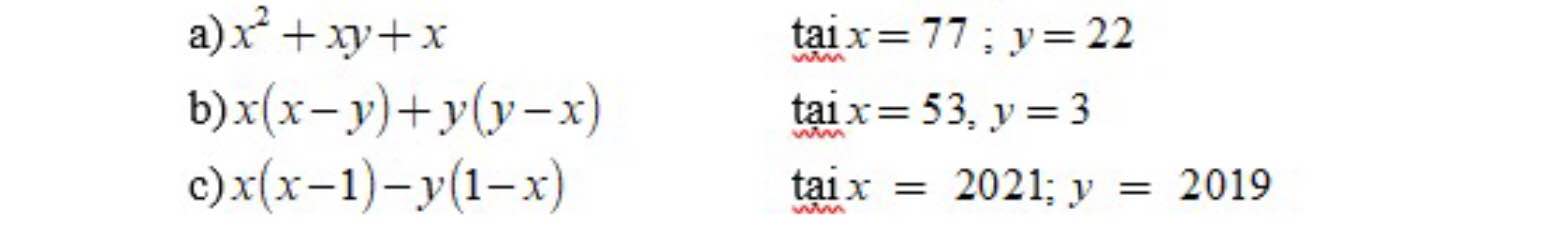 bài này nữa thôi các anh chị :3 em cảm ơn nhiều ạ
bài này nữa thôi các anh chị :3 em cảm ơn nhiều ạ