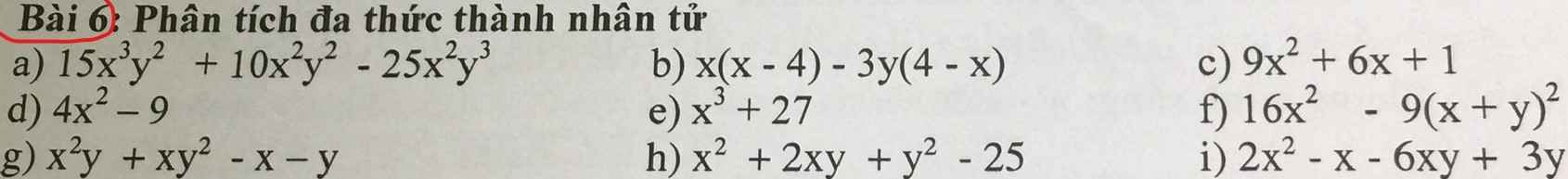Câu 1:Tìm giá trị nhỏ nhất của biểu thức:
A=x2-2x+2
Ta có: \(A=x^2-2x+2=\left(x^2-2x+1\right)+1=\left(x-1\right)^2+1\)
Mà: \(\left(x-1\right)^2\ge0,\forall x\)
\(\Rightarrow\left(x-1\right)^2+1\ge1,\forall x\)
Hay \(A\ge1,\forall x\)
Dấu "=" xảy ra\(\Leftrightarrow x-1=0\Leftrightarrow x=1\)
Vậy Min A=1 tại x=-1.
Câu 2:Rút gọn rồi tính giá trị của biểu thức sau:
(x-y).(x2+xy+y2)+2y3 tại x=2/3 và y=1/3
Đặt A=(x-y).(x2+xy+y2)+2y3
Ta có:A= (x-y).(x2+xy+y2)+2y3=\(x^3-y^3+2y^3=x^3+y^3\)(*)
Thay \(x=\frac{2}{3};y=\frac{1}{3}\) vào (*) ta có:
\(A=\left(\frac{2}{3}\right)^3+\left(\frac{1}{3}\right)^3=\frac{2^3+1^3}{3^3}=\frac{9}{27}=\frac{1}{3}\)
Vậy A=1/3
Câu 3:Phân tích đa thức sau thành nhân tử:
a/ 4x-8y=4(x-2y)
b/ x2+2xy+y2=\(\left(x+y\right)^2\)
c/ 2xy+3zy+6y+x2 (mk chịu =.=)
Câu 2:
\(=x^3-y^3+2y^3=x^3+y^3=\dfrac{8}{27}+\dfrac{1}{27}=\dfrac{9}{27}=\dfrac{1}{3}\)
Câu 1:
\(A=x^2-2x+2\)
=x^2-2x+1+1
=(x-1)^2+1>=1
Dấu = xảy ra khi x=1