a)
Ta có x = 20 \(\Rightarrow\)x+1=21
A = \(x^4-x^3.\left(x+1\right)+x^2.\left(x+1\right)-x\left(x+1\right)+2020\)
A = \(x^4-x^4-x^3+x^3+x^2-x^2-x+2020\)
A = 2020\(-\)x
Thay x = 20 vào biểu thức A ta có:
A = 2020 \(-20\)
A = 2000
Vậy biểu thức A = 2000 khi x = 20.
b.
Ta có x =2020 \(\Rightarrow a+1=2023\)
\(C=x^{2022}-x^{2021}.\left(x+1\right)+x^{2020}\left(x+1\right)-...+x^2.\left(x+1\right)-x.\left(x+1\right)+x+1\)
\(C=x^{2022}-x^{2022}-x^{2021}+x^{2021}+...+x^3+x^2-x^2-x+x+1\)
\(C=1\)
a: x=20 nên x+1=21
\(A=x^4-x^3\left(x+1\right)+x^2\left(x+1\right)-x\left(x+1\right)+2020\)
\(=x^4-x^4-x^3+x^3+x^2-x^2-x+2020\)
=2020-x=2000
b: \(x=2022\) nên x+1=2023
\(C=x^{2022}-x^{2021}\left(x+1\right)+x^{2020}\left(x+1\right)-...+x^2\left(x+1\right)-x\left(x+1\right)+x+1\)
\(=x^{2022}-x^{2022}-x^{2021}+x^{2021}+...+x^3+x^2-x^2-x+x+1\)
=1
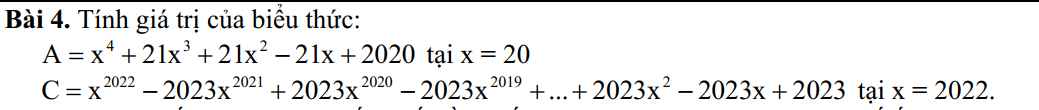




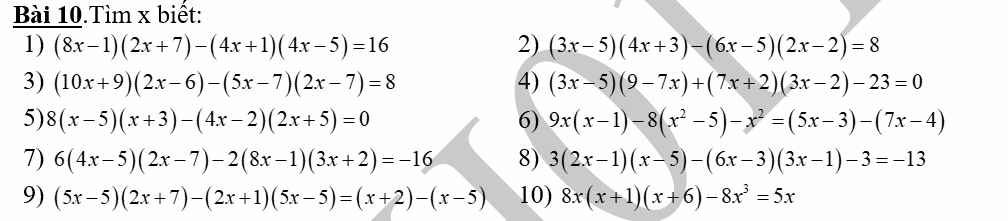 giúp em câu 6,9,10 câu này khó em k làm dc
giúp em câu 6,9,10 câu này khó em k làm dc
