\(6x^2+xy-7x-2y^2+7y-5=-\left(y-2x-1\right)\left(2y+3x-5\right)\)
\(6x^2+xy-7x-2y^2+7y-5=-2y\left(y-2x-1\right)-3x\left(y-2x-1\right)+5\left(y-2x-1\right)=-\left(y-2x-1\right)\left(2y+3x-5\right)\)
\(6x^2+xy-7x-2y^2+7y-5\)
\(=\left(2y+3x-5\right)\cdot\left(-y+2x+1\right)\)
Lời giải này sử dụng phương pháp hệ số bất định. Bạn có thể tham khảo thêm tại sách nâng cao phát triển toán 8 hoặc google.
Dù đã gắn tag phân tích đa thức thành nhân tử nhưng đề bài em vẫn nên viết đầy đủ yêu cầu đề.
Lời giải:
Đặt
$6x^2+xy-7x-2y^2+7y-5=(2x+ay+b)(3x+cy+d)$ với $a,b,c,d$ là số nguyên
$6x^2+xy-7x-2y^2+7y-5=6x^2+(2c+3a)xy+(2d+3b)x+(ad+bc)y+acy^2+bd$
Đồng nhất hệ số:
\(\left\{\begin{matrix} 2c+3a=1\\ 2d+3b=-7\\ ad+bc=7\\ ac=-2\\ bd=-5\end{matrix}\right.\)
Vì $ac=-2$; $2c+3a=1$ nên $a$ lẻ.
Do đó: $(a,c)=(-1,2); (1,-2)$. Thử vào hpt ta thấy $a=-1; c=2$
$bd=-5$ kết hợp $2d+3b=-7$ suy ra $b=1; d=-5$
Vậy $6x^2+xy-7x-2y^2+7y-5=(2x-y+1)(3x+2y-5)$




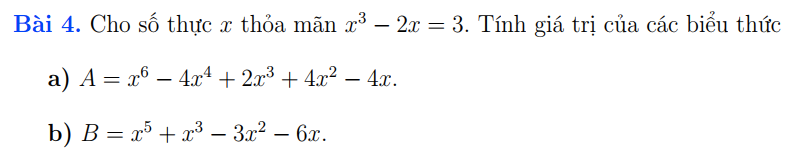
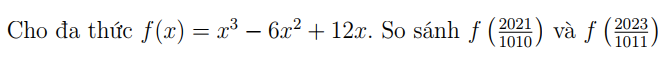
 Giúp e với ạ
Giúp e với ạ