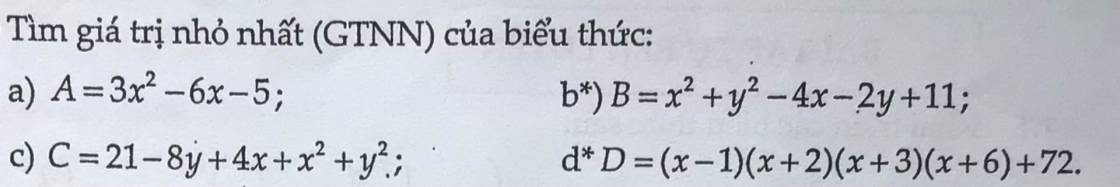a)
\(A=3x^2-6x-5\\ =3\left(x^2-2x-\dfrac{5}{3}\right)\\ =3\left(x^2-2x+1\right)-8\\ =3\left(x-2\right)^2-8\ge-8\)
GTNN của A đạt `-8` khi và chỉ khi `x=2`
b)
\(B=x^2+y^2-4x-2y+11\\ =x^2-4x+4+y^2-2y+1+6\\ =\left(x-2\right)^2+\left(y-1\right)^2+6\ge6\)
GTNN của B đạt `6` khi và chỉ khi \(\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
c)
\(C=21-8y+4x+x^2+y^2\\ =x^2+4x+4+y^2-8y+16+1\\ =\left(x+2\right)^2+\left(y-4\right)^2+1\ge1\)
GTNN của C đạt `1` khi và chỉ khi \(\left\{{}\begin{matrix}x=-2\\y=4\end{matrix}\right.\)
d)
\(D=\left(x-1\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)+72\\ =\left(x-1\right)\left(x+6\right)\left(x+2\right)\left(x+3\right)+72\\ =\left(x^2+5x-6\right)\left(x^2+5x+6\right)+72\\ =\left(x^2+5x\right)^2-36+72\\ =\left(x^2+5x\right)^2+36\ge36\)
GTNN của D đạt `36` khi và chỉ khi \(\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)