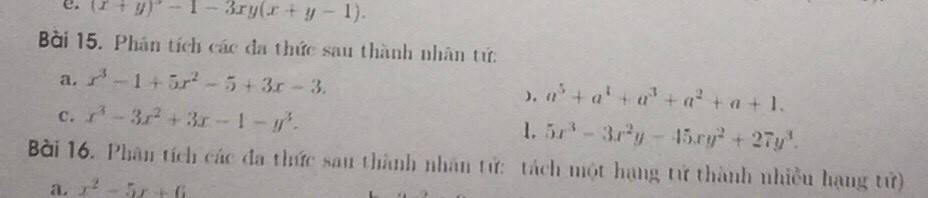Question

Answer 1

a: =(x^3-1)+5(x^2-1)+3(x-1)

=(x-1)(x^2+x+1)+(x-1)(5x+5)+3(x-1)

=(x-1)(x^2+x+1+5x+5+3)

=(x-1)(x^2+6x+9)

=(x-1)(x+3)^2

b: =a^4(a+1)+a^2(a+1)+(a+1)

=(a+1)(a^4+a^2+1)

=(a+1)(a^4+2a^2+1-a^2)

=(a+1)[(a^2+1)^2-a^2]

=(a+1)(a^2+1-a)(a^2+1+a)

c: =(x-1)^3-y^3

=(x-1-y)[(x-1)^2+y(x-1)+y^2]

=(x-y-1)(x^2-2x+1+xy-y+y^2)

d: =x^2(5x-3y)-9y^2(5x-3y)

=(5x-3y)(x^2-9y^2)

=(5x-3y)(x-3y)(x+3y)