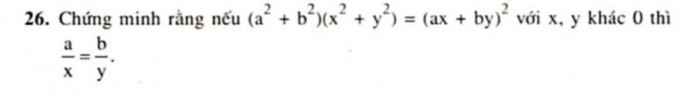\(\left(a^2+b^2\right)\left(x^2+y^2\right)=\left(ax+by\right)^2\)
\(\Leftrightarrow a^2x^2+a^2y^2+b^2x^2+b^2y^2=a^2x^2+2ax.by+b^2y^2\)
\(\Leftrightarrow a^2x^2-a^2x^2+a^2y^2+b^2x^2-2axby+b^2y^2-b^2y^2=0\)
\(\Leftrightarrow\left(ay\right)^2-2ay.bx+\left(bx\right)^2=0\)
\(\Leftrightarrow\left(ay-bx\right)^2=0\)
\(\Leftrightarrow ay-bx=0\)
\(\Leftrightarrow ay=bx\)
\(\Leftrightarrow\dfrac{ay}{xy}=\dfrac{bx}{xy}\)
\(\Leftrightarrow\dfrac{a}{x}=\dfrac{b}{y}\)