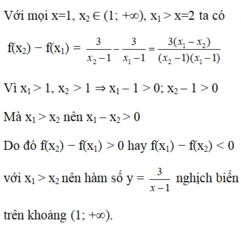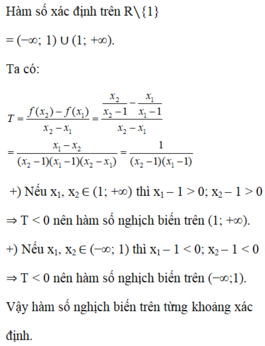Xét sự biến thiên của hàm số y=
MT
Những câu hỏi liên quan
Xét sự biến thiên của hàm số y = 3 x − 1 trên khoảng (1; + ∞ )
A. Đồng biến
B. Nghịch biến
C. Vừa đồng biến, vừa nghịch biến
D. Không đồng biến, cũng không nghịch biến
Xét sự biến thiên của hàm số
y
x
x
−
1
. Chọn khẳng định đúng. A. Hàm số nghịch biến trên từng khoảng xác định của nó B. Hàm số đồng biến trên từng khoảng xác định của nó. C. Hàm số đồng biến trên (−
∞
; 1), nghịch biến trên (1; +
∞
). D. Hàm số nghịch biến trên
(
−
∞
;
1...
Đọc tiếp
Xét sự biến thiên của hàm số y = x x − 1 . Chọn khẳng định đúng.
A. Hàm số nghịch biến trên từng khoảng xác định của nó
B. Hàm số đồng biến trên từng khoảng xác định của nó.
C. Hàm số đồng biến trên (− ∞ ; 1), nghịch biến trên (1; + ∞ ).
D. Hàm số nghịch biến trên ( − ∞ ; 1 ) ∪ ( 1 ; + ∞ ) .
Xét sự biến thiên của hàm số
y
1
x
2
. Mệnh đề nào sau đây đúng? A. Hàm số đồng biến trên (−
∞
; 0), nghịch biến trên (0; +
∞
). B. Hàm số đồng biến trên (0; +
∞
), nghịch biến trên (−
∞
; 0). C. Hàm số đồng biến trên (−
∞
; 1), nghịch biến trên (1; +
∞
). D. Hàm số nghịc...
Đọc tiếp
Xét sự biến thiên của hàm số y = 1 x 2 . Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên (− ∞ ; 0), nghịch biến trên (0; + ∞ ).
B. Hàm số đồng biến trên (0; + ∞ ), nghịch biến trên (− ∞ ; 0).
C. Hàm số đồng biến trên (− ∞ ; 1), nghịch biến trên (1; + ∞ ).
D. Hàm số nghịch biến trên ( − ∞ ; 0 ) ∪ ( 0 ; + ∞ ) .
Xét sự biến thiên của hàm số y sinx - cosx. Tìm kết luận nào đúng? A. Hàm số đã cho đồng biến trên khoảng (
-
π
4
;
3
π
4
) B. Hàm số đã cho đồng biến trên khoảng (
3
π
4
;
7
π
4
) C. Hàm số đã...
Đọc tiếp
Xét sự biến thiên của hàm số y = sinx - cosx. Tìm kết luận nào đúng?
A. Hàm số đã cho đồng biến trên khoảng ( - π 4 ; 3 π 4 )
B. Hàm số đã cho đồng biến trên khoảng ( 3 π 4 ; 7 π 4 )
C. Hàm số đã cho có tập giá trị là [-1; 1]
D. Hàm số đã cho luôn nghịch biến trên khoảng ( - π 4 ; 7 π 4 )
Cho hàm số: y = 4 x 3 + mx (m là tham số) (1)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với m = 1.
b) Viết phương trình tiếp tuyến của (C) song song với đường thẳng y = 13x + 1.
c) Xét sự biến thiên của hàm số (1) tùy thuộc vào giá trị m.
a) y = 4 x 3 + x, y′ = 12 x 2 + 1 > 0, ∀ x ∈ R
Bảng biến thiên:
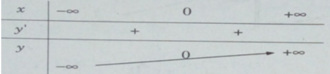
Đồ thị:
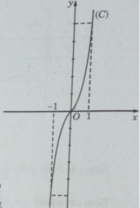
b) Giả sử tiếp điểm cần tìm có tọa độ (x0; y0) thì f′(x0) = 12 x 0 2 + 1 = 13 (vì tiếp tuyến song song với đường thẳng (d): y = 3x + 1). Từ đó ta có: x0 = 1 hoặc x0 = -1
Vậy có hai tiếp tuyến phải tìm là y = 13x + 8 hoặc y = 13x - 8
c) Vì y’ = 12 x 2 + m nên m ≥ 0; y” = –6( m 2 + 5m)x + 12m
+) Với m ≥ 0 ta có y’ > 0 (khi m = 0; y’ = 0 tại x = 0).
Vậy hàm số (1) luôn luôn đồng biến khi m ≥ 0; y” = –6( m 2 + 5m)x + 12m
+) Với m < 0 thì y = 0 ⇔ 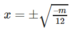
Từ đó suy ra:
y’ > 0 với

y’ < 0 với
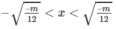
Vậy hàm số (1) đồng biến trên các khoảng
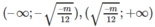
và nghịch biến trên khoảng
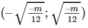
Đúng 0
Bình luận (0)
Xét sự biến thiên và vẽ đồ thị của các hàm số sau:
a) y=x2-2x
c) y=2x2+6x+3
Cho hàm số: y = 4 x 3 + mx (m là tham số) (1). Xét sự biến thiên của hàm số (1) tùy thuộc vào giá trị m.
Vì y’ = 12 x 2 + m nên m ≥ 0; y” = –6( m 2 + 5m)x + 12m
+) Với m ≥ 0 ta có y’ > 0 (khi m = 0; y’ = 0 tại x = 0).
Vậy hàm số (1) luôn luôn đồng biến khi m ≥ 0; y” = –6( m 2 + 5m)x + 12m
+) Với m < 0 thì y = 0 ⇔ 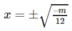
Từ đó suy ra:
y’ > 0 với

y’ < 0 với
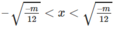
Vậy hàm số (1) đồng biến trên các khoảng
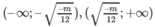
và nghịch biến trên khoảng
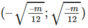
Đúng 0
Bình luận (0)
Xét sự biến thiên của hàm số y sinx - cosx. Trong các kết luận sau, kết luận nào đúng? A. Hàm số đã cho đồng biến trên khoảng (
-
π
4
;
3
π
4
) B. Hàm số đã cho đồng biến trên khoảng (
3
π
4
;
7
π
4
) C. Hàm s...
Đọc tiếp
Xét sự biến thiên của hàm số y = sinx - cosx. Trong các kết luận sau, kết luận nào đúng?
A. Hàm số đã cho đồng biến trên khoảng ( - π 4 ; 3 π 4 )
B. Hàm số đã cho đồng biến trên khoảng ( 3 π 4 ; 7 π 4 )
C. Hàm số đã cho có tập giá trị là [-1; 1]
D. Hàm số đã cho luôn nghịch biến trên khoảng ( - π 4 ; 7 π 4 )
Đáp án A
Ta có y = sin x - cos x = 2 sin x - π 4
Từ đây ta có thể loại đáp án C, do tập giá trị của hàm số là - 2 ; 2
Hàm số đã cho tuần hoàn với chu kỳ 2π do vậy ta xét sự biến thiên của hàm số trên đoạn (-π/4; 7π/4)
Ta có:
* Hàm số đồng biến trên khoảng (-π/4; 3π/4)
* Hàm số nghịch biến trên khoảng (3π/4; 7π/4)
Đúng 0
Bình luận (0)
Xét sự biến thiên của hàm số sau:
sin2x-2cosx-2x
\(y'=2\left(cos2x+sinx-1\right)=2\left(-2sin^2x+sinx\right)\)
\(y'=0\Rightarrow\left[{}\begin{matrix}sinx=0\\sinx=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
Hàm đồng biến trên các khoảng: \(\left(k2\pi;\dfrac{\pi}{6}+k2\pi\right)\) ; \(\left(\dfrac{5\pi}{6}+k2\pi;\pi+k2\pi\right)\)
Hàm nghịch biến trên các khoảng: \(\left(\dfrac{\pi}{6}+k2\pi;\dfrac{5\pi}{6}+k2\pi\right)\) ; \(\left(-\pi+k2\pi;k2\pi\right)\)
Đúng 0
Bình luận (0)