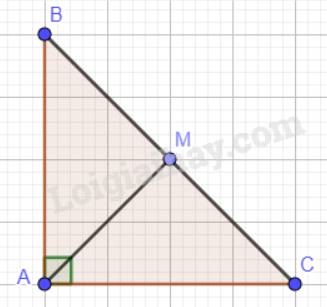
Cho tam giác ABC vuông cân tại A. Gọi M là trung điểm cạnh BC ; I là trung điểm cạnh AC ; E là điểm đối xứng với M qua I
a) Tứ giác AMCE là hình gì ? Tại sao ?
b) Tính diện tích tứ giác AMCE và diện tích tứ giác ABCE biết cạnh BC = 5cm
Mọi người giúp mik giải nha còn hình mik biết vẽ rồi