Cho \(a,b,c\in\left[1;2\right]\).Chứng minh : \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\le\frac{81}{8}\)
BQ
Những câu hỏi liên quan
1. Cho \(A=\left\{x\in N|x⋮6\right\}\); \(B=\left\{x\in N|x⋮15\right\}\); \(C=\left\{x\in N|x⋮30\right\}\)
CMR: \(C=A\cap B\)
Có các phần tử của A là bội của 6
Các phần tử của B là bội của 15
Các phần tử của C là bội của 30
mà [6;15]=30
=> Những phần tử vừa chia hết cho 6; vừa chia hết cho 15 thì sẽ chia hết cho 30
Hay \(C=A\cap B\)
Đúng 1
Bình luận (0)
cho \(a,b,c\in\left[0,1\right].CMR:\frac{a}{b+c+1}+\frac{b}{a+c+1}+\frac{c}{a+b+1}+\left(1-a\right)\left(1-b\right)\left(1-c\right)\le1\)
1) Cho a, b, c 0. Chứng minh: left(frac{a}{b}+frac{b}{c}+frac{c}{a}right)^2geleft(a+b+cright)left(frac{1}{a}+frac{1}{b}+frac{1}{c}right)2) Cho a,b,cin R.a) Chứng minh: left(a^2+3right)left(b^2+3right)left(c^2+3right)ge4left(a+b+c+1right)^2b) Chứng minh: left(a^2+1right)left(b^2+1right)left(c^2+1right)gefrac{5}{16}left(a+b+c+1right)^23) Cho a,b,cin RChứng minh: frac{a^3}{b^2}+frac{b^3}{c^2}+frac{c^3}{a^2}gefrac{a^2}{b}+frac{b^2}{c}+frac{c^2}{a}
Đọc tiếp
1) Cho a, b, c > 0. Chứng minh: \(\left(\frac{a}{b}+\frac{b}{c}+\frac{c}{a}\right)^2\ge\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)
2) Cho \(a,b,c\in R\).
a) Chứng minh: \(\left(a^2+3\right)\left(b^2+3\right)\left(c^2+3\right)\ge4\left(a+b+c+1\right)^2\)
b) Chứng minh: \(\left(a^2+1\right)\left(b^2+1\right)\left(c^2+1\right)\ge\frac{5}{16}\left(a+b+c+1\right)^2\)
3) Cho \(a,b,c\in R\)Chứng minh: \(\frac{a^3}{b^2}+\frac{b^3}{c^2}+\frac{c^3}{a^2}\ge\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}\)
2) Theo nguyên lí Dirichlet, trong ba số \(a^2-1;b^2-1;c^2-1\) có ít nhất hai số nằm cùng phía với 1.
Giả sử đó là a2 - 1 và b2 - 1. Khi đó \(\left(a^2-1\right)\left(b^2-1\right)\ge0\Leftrightarrow a^2b^2-a^2-b^2+1\ge0\)
\(\Rightarrow a^2b^2+3a^2+3b^2+9\ge4a^2+4b^2+8\)
\(\Rightarrow\left(a^2+3\right)\left(b^2+3\right)\ge4\left(a^2+b^2+2\right)\)
\(\Rightarrow\left(a^2+3\right)\left(b^2+3\right)\left(c^2+3\right)\ge4\left(a^2+b^2+1+1\right)\left(1+1+c^2+1\right)\) (2)
Mà \(4\left[\left(a^2+b^2+1+1\right)\left(1+1+c^2+1\right)\right]\ge4\left(a+b+c+1\right)^2\) (3)(Áp dụng Bunhicopxki và cái ngoặc vuông)
Từ (2) và (3) ta có đpcm.
Sai thì chịu
Đúng 0
Bình luận (0)
Xí quên bài 2 b:v
b) Không mất tính tổng quát, giả sử \(\left(a^2-\frac{1}{4}\right)\left(b^2-\frac{1}{4}\right)\ge0\)
Suy ra \(a^2b^2-\frac{1}{4}a^2-\frac{1}{4}b^2+\frac{1}{16}\ge0\)
\(\Rightarrow a^2b^2+a^2+b^2+1\ge\frac{5}{4}a^2+\frac{5}{4}b^2+\frac{15}{16}\)
Hay \(\left(a^2+1\right)\left(b^2+1\right)\ge\frac{5}{4}\left(a^2+b^2+\frac{3}{4}\right)\)
Suy ra \(\left(a^2+1\right)\left(b^2+1\right)\left(c^2+1\right)\ge\frac{5}{4}\left(a^2+b^2+\frac{1}{4}+\frac{1}{2}\right)\left(\frac{1}{4}+\frac{1}{4}+c^2+\frac{1}{2}\right)\)
\(\ge\frac{5}{4}\left(\frac{1}{2}a+\frac{1}{2}b+\frac{1}{2}c+\frac{1}{2}\right)^2=\frac{5}{16}\left(a+b+c+1\right)^2\) (Bunhiacopxki) (đpcm)
Đẳng thức xảy ra khi \(a=b=c=\frac{1}{2}\)
Đúng 0
Bình luận (0)
Cách nữa cho bài 2:
2a) Ta có: \(4\left(a^2+1+2\right)\left(1+1+\frac{\left(b+c\right)^2}{2}\right)\ge4\left(a+b+c+1\right)^2\)
Hay \(4\left(a^2+3\right)\left(2+\frac{\left(b+c\right)^2}{2}\right)\ge4\left(a+b+c+1\right)^2=VP\)
Như vậy ta quy bài toán về chứng minh: \(\left(b^2+3\right)\left(c^2+3\right)\ge4\left(2+\frac{\left(b+c\right)^2}{2}\right)\)
\(\Leftrightarrow b^2c^2+b^2+c^2+1\ge4bc\Leftrightarrow\left(bc-1\right)^2+\left(b-c\right)^2\ge0\)(đúng)
Đẳng thức xảy ra khi a = b = c = 1
b) Áp dụng BĐT Bunhiacopxki:\(\left(a^2+\frac{1}{4}+\frac{1}{4}+\frac{1}{2}\right)\left(\frac{1}{4}+b^2+c^2+\frac{1}{2}\right)\ge\frac{1}{4}\left(a+b+c+1\right)^2\)
\(\Rightarrow\frac{5}{4}\left(a^2+1\right)\left(b^2+c^2+\frac{3}{4}\right)\ge\frac{5}{16}\left(a+b+c+1\right)^2\)
Từ đó ta có thể quy bài toán về chứng minh: \(\left(b^2+1\right)\left(c^2+1\right)\ge\frac{5}{4}\left(b^2+c^2+\frac{3}{4}\right)\)
...
Bài 3:Sửa đề a, b, c >0
Có: \(\frac{a^3}{b^2}+\frac{a^3}{b^2}+b\ge3\sqrt[3]{\frac{a^6}{b^3}}=\frac{3a^2}{b}\)
Tương tự: \(\frac{2b^3}{c^2}+c\ge\frac{3b^2}{c};\frac{2c^3}{a^2}+a\ge\frac{3c^2}{a}\)
Cộng theo vế 3 BĐT trên: \(2\left(\frac{a^3}{b^2}+\frac{b^3}{c^2}+\frac{c^3}{a^2}\right)+a+b+c\ge3\left(\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}\right)\)
\(=2\left(\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}\right)+\left(\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}\right)\)
\(\ge2\left(\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}\right)+a+b+c\)
Từ đó ta có đpcm.
Cho tam giác \(ABC\). Lấy điểm \(M\) trên cạnh \(AC\) kéo dài (Hình 1). Mệnh đề nào sau đây là mệnh đề sai?
A. \(M \in \left( {ABC} \right)\).
B. \(C \in \left( {ABM} \right)\).
C. \(A \in \left( {MBC} \right)\).
D. \(B \in \left( {ACM} \right)\).
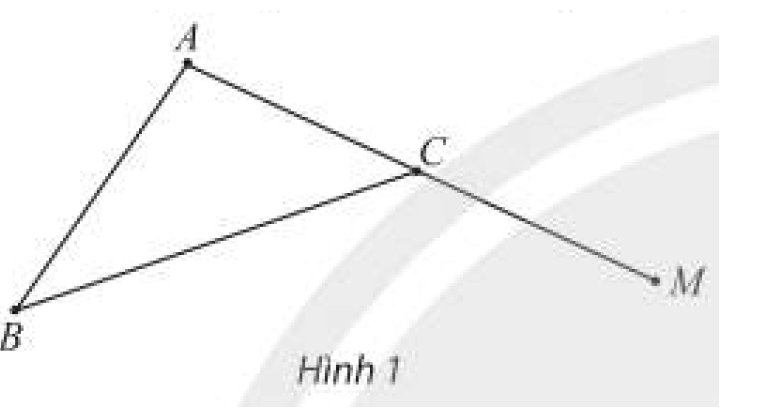
\(\left. \begin{array}{l}M \in AC\\AC \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow M \in \left( {ABC} \right)\). Vậy mệnh đề A đúng.
\(\left. \begin{array}{l}C \in AM\\AM \subset \left( {ABM} \right)\end{array} \right\} \Rightarrow C \in \left( {ABM} \right)\). Vậy mệnh đề B đúng.
\(\left. \begin{array}{l}A \in CM\\CM \subset \left( {MBC} \right)\end{array} \right\} \Rightarrow A \in \left( {MBC} \right)\). Vậy mệnh đề C đúng.
Vậy mệnh đề D sai.
Chọn D.
Đúng 0
Bình luận (0)
Cho a,b,c \(\in\) N. Chứng minh: \(\sqrt{a\left(b+1\right)}+\sqrt{b\left(c+1\right)}+\sqrt{c\left(a+1\right)}\le\dfrac{3}{2}.\sqrt{\left(a+1\right)\left(b+1\right)\left(c+1\right)}\)
Cho a,c,b \(\in\left[0;1\right]\)Chứng minh rằng :\(\frac{a}{b+c+1}+\frac{b}{a+c+1}+\frac{c}{a+b+1}+\left(1-a\right)\left(1-b\right)\left(1-c\right)\le1\)
(d) qua A(5; 6) : y = mx - 5m + 6 (1)
(C) : (x - 1)² + (y - 2)² = 1 (2)
Thay y từ (1) vào (2) ta có phương trình hoành độ giao điểm của (d) và (C)
(x - 1)² + (mx - 5m + 4)² = 1
Khai triển ra pt bậc 2 : (m² + 1)x² - 2(5m² - 4m + 1)x + 25m² - 40m + 17 = 0 (*)
Để (d) tiếp xúc (C) thì (*) phải có nghiệm kép
∆' = (5m² - 4m + 1)² - (m² + 1)(25m² - 40m + 17) = - 4(3m² - 8m + 4) = 4(m - 2)(2 - 3m) = 0 => m = 3/2; m = 2
KL : Có 2 đường thẳng cần tìm
(d1) : y = (3/2)(x - 1)
(d2) : y = 2x - 4
∆ ∠ ∡ √ ∛ ∜ x² ⁻¹ ∫ π × ∵ ∴ | | , ⊥,∈∝ ≤ ≥− ± , ÷ ° ≠ → ∞, ≡ , ≅ , ∑,∪,¼ , ½ , ¾ , ≈ , [-b ± √(b² - 4ac) ] / 2a Σ Φ Ω α β γ δ ε η θ λ μ π ρ σ τ φ ω ё й½ ⅓ ⅔ ¼ ⁰ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ⁺ ⁻ ⁼ ⁽ ⁾ ⁿ ₁ ₂ ₃₄₅ ₆ ₇ ₈ ₉ ₊ ₋ ₌ ₍ ₎ ∊ ∧ ∏ ∑ ∠ ,∫ ∫ ψ ω Π∮ ∯ ∰ ∇ ∂ • ⇒ ♠ ★
Đúng 0
Bình luận (0)
tjc4 vweftbf3sgrhrbn dkgmny09-695th shtyrdu495p6by
irevbfgt4t6w3tb2fygye-5gnft94v5e4gdentv4grdmnu4
Xem thêm câu trả lời
Cho a;b;c\(\in\)R .CMR \(2\left(1+abc\right)+\sqrt{2\left(1+a^2\right)\left(1+b^2\right)\left(1+c^2\right)}\ge\left(1+a\right)\left(1+b\right)\left(1+c\right)\)
\(2\left(1+abc\right)+\sqrt{2\left(1+a^2\right)\left(1+b^2\right)\left(1+c^2\right)}\)
\(=2\left(1+abc\right)+\sqrt{\left[\left(a+1\right)^2+\left(1-a\right)^2\right]\left[\left(b+c\right)^2+\left(bc-1\right)^2\right]}\)
\(\ge2\left(1+abc\right)+\left(a+1\right)\left(b+c\right)+\left(1-a\right)\left(bc-1\right)\)
\(=\left(1+a\right)\left(1+b\right)\left(1+c\right)\)
Đúng 0
Bình luận (0)
\(2\left(1+abc\right)+\sqrt{2\left(1+a^2\right)\left(1+b^2\right)\left(1+c^2\right)}.\)
\(=2\left(1+abc\right)+\sqrt{\left[\left(a+1\right)^2+\left(1-a\right)^2\right]\left[\left(b+c\right)^2+\left(bc-1\right)^2\right]}\)
\(\ge2\left(1+abc\right)+\left(a+1\right)\left(b+c\right)+\left(1-a\right)\left(bc-1\right)\)
\(=\left(1+a\right)\left(1+b\right)\left(1+c\right)\)
Đúng 0
Bình luận (0)
Cho a,b,c \(\in R^+\) và a.b.c=1. Chứng minh rằng:
\(\frac{a}{\left(a+1\right)\left(b+1\right)}+\frac{b}{\left(b+1\right)\left(c+1\right)}+\frac{c}{\left(c+1\right)\left(a+1\right)}\ge\frac{3}{4}\)
Lời giải:
\(\frac{a}{(a+1)(b+1)}+\frac{b}{(b+1)(c+1)}+\frac{c}{(c+1)(a+1)}\geq \frac{3}{4}\)
\(\Leftrightarrow \frac{a(c+1)+b(a+1)+c(b+1)}{(a+1)(b+1)(c+1)}\geq \frac{3}{4}\)
\(\Leftrightarrow 4[a(c+1)+b(a+1)+c(b+1)]\geq 3(a+1)(b+1)(c+1)\)
\(\Leftrightarrow 4(ab+bc+ac+a+b+c)\geq 3[(ab+bc+ac)+(a+b+c)+abc+1]\)
\(\Leftrightarrow ab+bc+ac+a+b+c\geq 3(abc+1)=6\)
Điều này luôn đúng do theo BĐT AM-GM thì \(ab+bc+ac+a+b+c\geq 6\sqrt[6]{(abc)^3}=6\)
Ta có đpcm. Dấu "=" xảy ra khi $a=b=c=1$
Đúng 0
Bình luận (0)
Cho tập \(A=\left(-\infty,-1\right)\cup\left(2,+\infty\right)\\ B=\left[-3.1\right]\)
Tìm m để \(C\dfrac{A}{B}\subset C\) biết \(C=\left\{x\in R\left|\left|2x-1\right|\le m\right|\right\}\)
Cho a,b,c \(\in\) Q thỏa mãn a.b+b.c+c.a =1
CM:\(\sqrt{\left(a^2+1\right).\left(b^2+1\right).\left(c^2+1\right)}\in Q\)
thay trực tiếp giả thiết ta có
\(\sqrt{\left(a^2+1\right)}=\sqrt{a^2+ab+bc+ac}=\sqrt{a\left(a+b\right)+c\left(a+b\right)}=\sqrt{\left(a+c\right)\left(a+b\right)}\)
tương tự ta có
\(\sqrt{b^2+1}=\sqrt{\left(b+a\right)\left(b+c\right)}\)
\(\sqrt{c^2+1}=\sqrt{\left(c+a\right)\left(c+b\right)}\)
nên
\(\sqrt{\left(a^2+1\right)\left(b^2+1\right)\left(c^2+1\right)}=\sqrt{\left(\left(a+b\right)\left(a+c\right)\left(b+c\right)\right)^2}=\left|\left(a+b\right)\left(a+c\right)\left(b+c\right)\right|\)
mà \(a,b,c\in Q\) nên \(\left|\left(a+b\right)\left(a+c\right)\left(b+c\right)\right|\in Q\Rightarrowđpcm\)
Đúng 0
Bình luận (0)



