Cho hàm số được xác định như sau:y = f (x) =x+1 khi x lớn hơn hoặc bằng 0; -x+1 khi x<0
a) Tính f (3); f (-3)
b) Có cách nào viết gọn công thức trên không?
GO
Những câu hỏi liên quan
a)Cho hàm số f(x)=ax^2+bx+c là các số hữu thỉ .Chứng tỏ rằng f(-2),f(3)lớn hơn hoặc bằng 0 biết rằng 13a+b+2c=0
b)Cho hàm số f(x) xác định với mọi x thuộc R .Biết rằng với mọi x ta đều có f(x)+3*f(1/x)=x^2
Cho hàm số y=f(x) được tinh bởi công thức:
f(x)= x + 1 nếu x lớn hơn hoặc bằng 0
f(x)= 1 - 2x nếu x<0
Tính f(2009) và f( -1004)
Do 2009 > 0 \(\Rightarrow f\left(2009\right)=2009+1=2010\)
DO -1004 < 0 \(\Rightarrow f\left(-1004\right)=1-2\cdot\left(-1004\right)=2009\)
Đúng 1
Bình luận (0)
vẽ độ thị hàm số : y= f(x)={-x khi x nhỏ hơn và bằng 0; -x^2+2x khi x lớn hơn 0
dựa vào đồ thị, xác định m để phương trình: f(x)=m có nghiệm 3
ĐỪNG CÓ NÓI ĐÂY LÀ BÀI KO GIẢI ĐƯỢC
Bài dễ thế này hỏi gì nữa thớt?
Vẽ đồ thị ra là làm được ngay.
Đúng 0
Bình luận (0)
tôi học lớp 7 đươc chưa cái thằng quỷ
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hàm số y=f(x) được tinh bởi công thức:
f(x)= x + 1 nếu x lớn hơn hoặc bằng 0
f(x)= 1 - 2x nếu x<0
Tính f(2009) và f( -1004)
f(x)=x+1\(\ge\)0
Thay f(2009)=2009+1\(\ge\)0
\(\Rightarrow\)2009+1=2010
Vậy : f(2009)=2009+1\(>\)0
Mấy các kia lm tương tự l đc
Đúng 0
Bình luận (0)
. Cho hàm số được xác định như sau : y = f(x) = \(\left\{\dfrac{x+1\text{ khi }\ge0}{-x+1\text{ khi }< 0}\right\}\)
a) Tính f(3); f(-3).
b) Có cách nào viết gọn công thức trên không ?
\(a,f\left(3\right)=3+1=4\\ f\left(-3\right)=3+1=4\\ b,y=f\left(x\right)=\left|x\right|+1\)
Đúng 2
Bình luận (0)
tìm tập xác định của hàm số sau:
y=\(\dfrac{x-1}{x^2-4}\)
ĐKXĐ: \(x^2-4\ne0\)
=>\(x^2\ne4\)
=>\(x\notin\left\{2;-2\right\}\)
vậy: TXĐ là D=R\{2;-2}
Đúng 0
Bình luận (0)
Cho hàm số f(x)=x+1 nếu x lớn hơn hoặc bằng 0 và 1-2x nếu x<0. tính f(2);f(-2);f(0);f(1/2)
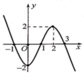
Cho hàm số
y
f
(
x
)
xác định và liên tục trên R. Đồ thị của hàm số f(x) như hình bên. Số nghiệm thực âm của phương trình
f
(
f
(
x
)
)
0
bằng? A. m 2 B. m 3 C. m 7 D. m 5
Đọc tiếp
Cho hàm số y = f ( x ) xác định và liên tục trên R. Đồ thị của hàm số f(x) như hình bên. Số nghiệm thực âm của phương trình f ( f ( x ) ) = 0 bằng?
A. m = 2
B. m = 3
C. m = 7
D. m = 5
H24
11 tháng 5 2021 lúc 9:54
Cho hàm số yf(x) xác định trên R và có bảng xét dấu đạo hàm như sau: x -∞ -1 1 4 +∞ f(x) - 0 + 0 - 0 + Biết f(x)2 ∀xϵR Xét hàm số gleft(xright)fleft(3-2fleft(xright)right)-x^3+3x^2-2020 đồng biến, nghịch biến trên các khoảng nào?
Đọc tiếp
Cho hàm số y=f(x) xác định trên R và có bảng xét dấu đạo hàm như sau:
| x | -∞ -1 1 4 +∞ |
| f'(x) | - 0 + 0 - 0 + |
Biết f(x)>2 ∀xϵR Xét hàm số \(g\left(x\right)=f\left(3-2f\left(x\right)\right)-x^3+3x^2-2020\) đồng biến, nghịch biến trên các khoảng nào?
Bài này chỉ có thể trắc nghiệm (dựa vào kết quả trắc nghiệm để suy luận) chứ không thể giải tự luận
Vì với mỗi hàm \(f\left(x\right)\) khác nhau sẽ cho những khoảng đồng biến - nghịch biến của \(g\left(x\right)\) khác nhau
Đúng 0
Bình luận (0)