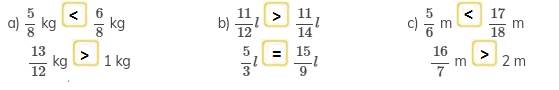Cho M=\(\dfrac{5}{11}+\dfrac{5}{12}+\dfrac{5}{13}+\dfrac{5}{14}\). Chứng tỏ rằng 1 < M < 2
HT
Những câu hỏi liên quan
chứng minh rằng
A= \(\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+...+\dfrac{1}{17}< 2\)
B=\(\dfrac{5}{11}+\dfrac{5}{12}+\dfrac{5}{13}+\dfrac{5}{14},1< B< 2\)
, , ?a) dfrac{5}{8} kg dfrac{6}{8} kg b) dfrac{11}{12}l dfrac{11}{14}l c) dfrac{5}{6} m dfrac{17}{18} m dfrac{13}{12} kg 1 kg dfrac{5}{3}l dfrac{15}{9}l dfrac{16}{7} m 2 m
Đọc tiếp
>, <, = ?
a) \(\dfrac{5}{8}\) kg  \(\dfrac{6}{8}\) kg b) \(\dfrac{11}{12}l\)
\(\dfrac{6}{8}\) kg b) \(\dfrac{11}{12}l\)  \(\dfrac{11}{14}l\) c) \(\dfrac{5}{6}\) m
\(\dfrac{11}{14}l\) c) \(\dfrac{5}{6}\) m  \(\dfrac{17}{18}\) m
\(\dfrac{17}{18}\) m
\(\dfrac{13}{12}\) kg  1 kg \(\dfrac{5}{3}l\)
1 kg \(\dfrac{5}{3}l\)  \(\dfrac{15}{9}l\) \(\dfrac{16}{7}\) m
\(\dfrac{15}{9}l\) \(\dfrac{16}{7}\) m  2 m
2 m
a)
\(\dfrac{5}{8}\left(kg\right)< \dfrac{6}{8}\left(kg\right)\)
Do 13 > 12 nên \(\dfrac{13}{12}>1\)
hay: \(\dfrac{13}{12}\left(kg\right)>1\left(kg\right)\)
b)
\(\dfrac{11}{12}\left(l\right)>\dfrac{11}{14}\left(l\right)\)
Có:
\(\dfrac{5}{3}=\dfrac{5\times3}{3\times3}=\dfrac{15}{9}\)
nên: \(\dfrac{5}{3}\left(l\right)=\dfrac{15}{9}\left(l\right)\)
c)
\(\dfrac{5}{6}=\dfrac{5\times3}{6\times3}=\dfrac{15}{18n}\)
nên \(\dfrac{5}{6}\left(m\right)< \dfrac{17}{8}\left(m\right)\)
Có: \(2=\dfrac{2\times7}{7}=\dfrac{14}{7}\)
nên: \(\dfrac{16}{7}\left(m\right)>2\left(m\right)\)
Đúng 2
Bình luận (0)
Chứng tỏ rằng: \(1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{19}-\dfrac{1}{20}=\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+...+\dfrac{1}{20}\)
\(1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{19}-\dfrac{1}{20}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{19}-\dfrac{1}{20}+\left(\dfrac{1}{2}-\dfrac{1}{2}\right)+\left(\dfrac{1}{4}-\dfrac{1}{4}\right)+...+\left(\dfrac{1}{20}-\dfrac{1}{20}\right)\)
\(=1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{20}-2\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{20}\right)\)
\(=1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{20}-\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{10}\right)\)
\(=\dfrac{1}{11}+\dfrac{1}{12}+...+\dfrac{1}{20}\) (đpcm)
Đúng 2
Bình luận (0)
dfrac{1}{5}+dfrac{2}{11} dfrac{x}{55} dfrac{2}{5}+dfrac{1}{5} dfrac{1}{2}+dfrac{1}{3}+dfrac{1}{6} xledfrac{13}{4}+dfrac{14}{8} dfrac{1}{4}+dfrac{5}{12}+dfrac{-1}{13} x dfrac{7}{5}+dfrac{2}{10}+dfrac{1}{2} dfrac{79}{15}+dfrac{7}{5}+dfrac{-8}{3}le xledfrac{10}{3}+dfrac{15}{4}+dfrac{23}{12}
Đọc tiếp
\(\dfrac{1}{5}+\dfrac{2}{11}< \dfrac{x}{55}< \dfrac{2}{5}+\dfrac{1}{5}\) \(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{6}< x\le\dfrac{13}{4}+\dfrac{14}{8}\)
\(\dfrac{1}{4}+\dfrac{5}{12}+\dfrac{-1}{13}< x< \dfrac{7}{5}+\dfrac{2}{10}+\dfrac{1}{2}\) \(\dfrac{79}{15}+\dfrac{7}{5}+\dfrac{-8}{3}\le x\le\dfrac{10}{3}+\dfrac{15}{4}+\dfrac{23}{12}\)
\(\dfrac{1}{5}+\dfrac{2}{11}< \dfrac{x}{55}< \dfrac{2}{5}+\dfrac{1}{5}\)
\(\dfrac{11+10}{55}< \dfrac{x}{55}< \dfrac{3}{5}\)
\(\dfrac{21}{55}< \dfrac{x}{55}< \dfrac{33}{55}\)
Vậy \(x\in\left\{22;23;24;...\right\}\)
Đúng 0
Bình luận (0)
\(\dfrac{????????}{????????????}\)
Đúng 0
Bình luận (0)
a) \(\dfrac{1}{5}+\dfrac{2}{11}< \dfrac{x}{55}< \dfrac{2}{5}+\dfrac{1}{5}\)
\(\dfrac{11}{55}+\dfrac{10}{55}< \dfrac{x}{55}< \dfrac{22}{55}+\dfrac{1}{55}\)
\(\dfrac{21}{55}< \dfrac{x}{55}< \dfrac{23}{55}\)
\(\Rightarrow\) \(x=22\)
b) \(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{6}< x\le\dfrac{13}{4}+\dfrac{14}{8}\)
\(\dfrac{3}{6}+\dfrac{2}{6}+\dfrac{1}{6}< x\le\dfrac{26}{8}+\dfrac{14}{8}\)
\(1< x\le5\)
\(\Rightarrow\) \(x\in\) {\(2;3;4;5\)}
c) \(\dfrac{1}{3}+\dfrac{5}{12}+\dfrac{-1}{13}< x< \dfrac{7}{5}+\dfrac{2}{10}+\dfrac{1}{2}\)
Ko biết làm
d) \(\dfrac{79}{15}+\dfrac{7}{5}+\dfrac{-8}{3}\le x\le\dfrac{10}{3}+\dfrac{15}{4}+\dfrac{23}{12}\)
\(\dfrac{79}{15}+\dfrac{21}{15}+\dfrac{-40}{15}\le x\le\dfrac{40}{12}+\dfrac{45}{12}+\dfrac{23}{12}\)
\(4\le x\le9\)
\(\Rightarrow\) \(x\in\) {\(4;5;6;7;8;9\)}
Đúng 1
Bình luận (0)
\(\dfrac{1}{5}\)+\(\dfrac{1}{13}\)+\(\dfrac{1}{25}\)+...+\(\dfrac{1}{10^2}\)+\(\dfrac{1}{11^2}\)< \(\dfrac{9}{20}\)
Chứng tỏ rằng biểu thức trên bé hơn 9/20
Thực hiện phép tính (tính hợp lý nếu có thể): a) dfrac{5}{9}.dfrac{7}{13}+dfrac{5}{9}.dfrac{8}{13}-dfrac{5}{13}.dfrac{2}{9} b) 12dfrac{5}{14}-left(3dfrac{5}{7}+5dfrac{5}{14}right) c)dfrac{-2}{5}+dfrac{7}{11}+dfrac{-11}{10}+dfrac{7}{-11} d) dfrac{1}{2}+dfrac{-2}{3}+dfrac{1}{6}+dfrac{-2}{5}
Đọc tiếp
Thực hiện phép tính (tính hợp lý nếu có thể):
a) \(\dfrac{5}{9}.\dfrac{7}{13}+\dfrac{5}{9}.\dfrac{8}{13}-\dfrac{5}{13}.\dfrac{2}{9}\) b) \(12\dfrac{5}{14}-\left(3\dfrac{5}{7}+5\dfrac{5}{14}\right)\)
c)\(\dfrac{-2}{5}+\dfrac{7}{11}+\dfrac{-11}{10}+\dfrac{7}{-11}\) d) \(\dfrac{1}{2}+\dfrac{-2}{3}+\dfrac{1}{6}+\dfrac{-2}{5}\)
b: =12+5/14-3-5/7-5-5/14
=4-5/7
=28/7-5/7=23/7
c: =(-2/5-11/10)+(7/11-7/11)
=-4/10-11/10=-15/10=-3/2
Đúng 3
Bình luận (0)
\(a,\dfrac{5}{9}\cdot\dfrac{7}{13}+\dfrac{5}{9}\cdot\dfrac{8}{13}-\dfrac{5}{13}\cdot\dfrac{2}{9}\)
\(=\dfrac{5}{9}\cdot\dfrac{7}{13}+\dfrac{5}{9}\cdot\dfrac{8}{13}-\dfrac{2}{13}\cdot\dfrac{5}{9}\)
\(=\dfrac{5}{9}\cdot\left(\dfrac{7}{13}+\dfrac{8}{13}-\dfrac{2}{13}\right)\)
\(=\dfrac{5}{9}\cdot\dfrac{14}{13}\)
\(=\dfrac{70}{117}\)
\(d,\dfrac{1}{2}+\dfrac{-2}{3}+\dfrac{1}{6}+\dfrac{-2}{5}\)
\(=\left(\dfrac{1}{2}+\dfrac{-2}{3}+\dfrac{1}{6}\right)+\dfrac{-2}{5}\)
\(=0+\dfrac{-2}{5}\)
\(=\dfrac{-2}{5}\)
Đúng 1
Bình luận (0)
Thực hiện phép tính( hợp lí nếu có thể)
dfrac{1}{2}+dfrac{3}{4}-left(dfrac{3}{4}-dfrac{4}{5}right)
dfrac{-3}{7}+dfrac{3}{4}:dfrac{3}{14}
5-dfrac{7}{39}:dfrac{7}{13}+dfrac{8}{9}:4
1dfrac{13}{15}.0,75-left(dfrac{11}{20}+25%right):dfrac{7}{3}
left(dfrac{5}{12}:dfrac{11}{6}+dfrac{5}{12}:dfrac{11}{5}right)--dfrac{7}{12}
làm nhanh cho mình nha!!!!Thank nhìu
Đọc tiếp
Thực hiện phép tính( hợp lí nếu có thể)
\(\dfrac{1}{2}+\dfrac{3}{4}-\left(\dfrac{3}{4}-\dfrac{4}{5}\right)\)
\(\dfrac{-3}{7}+\dfrac{3}{4}:\dfrac{3}{14}\)
\(5-\dfrac{7}{39}:\dfrac{7}{13}+\dfrac{8}{9}:4\)
\(1\dfrac{13}{15}.0,75-\left(\dfrac{11}{20}+25\%\right):\dfrac{7}{3}\)
\(\left(\dfrac{5}{12}:\dfrac{11}{6}+\dfrac{5}{12}:\dfrac{11}{5}\right)--\dfrac{7}{12}\)
làm nhanh cho mình nha!!!!Thank nhìu
\(\dfrac{1}{2}+\dfrac{3}{4}-\left(\dfrac{3}{4}-\dfrac{4}{5}\right)\\ =\dfrac{1}{2}+\dfrac{3}{4}-\dfrac{3}{4}+\dfrac{4}{5}\\ =\dfrac{1}{2}+\left(\dfrac{3}{4}-\dfrac{3}{4}\right)+\dfrac{4}{5}\\ =\dfrac{1}{2}+0+\dfrac{4}{5}\\ =\dfrac{1}{2}+\dfrac{4}{5}\\ =\dfrac{5}{10}+\dfrac{8}{10}\\ =\dfrac{13}{10}\)
Đúng 0
Bình luận (0)
\(\dfrac{-3}{7}+\dfrac{3}{4}:\dfrac{3}{14}\\ =\dfrac{-3}{7}+\dfrac{3}{4}\cdot\dfrac{14}{3}\\ =\dfrac{-3}{7}+\dfrac{7}{2}\\ =\dfrac{-6}{14}+\dfrac{49}{14}\\ =\dfrac{43}{14}\)
Đúng 0
Bình luận (0)
\(1\dfrac{13}{15}.0,75-\left(\dfrac{11}{20}+25\%\right):\dfrac{7}{3}\\ =\dfrac{28}{15}.\dfrac{3}{4}-\left(\dfrac{11}{20}+\dfrac{1}{4}\right):\dfrac{7}{3}\\ =\dfrac{7}{5}-\left(\dfrac{11}{20}+\dfrac{5}{20}\right):\dfrac{7}{3}\\ =\dfrac{7}{5}-\dfrac{4}{5}:\dfrac{7}{3}\\ =\dfrac{7}{5}-\dfrac{4}{5}.\dfrac{3}{7}\\ =\dfrac{7}{5}-\dfrac{12}{35}\\ =\dfrac{49}{35}-\dfrac{12}{35}\\ =\dfrac{37}{35}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng tỏ rằng:
\(\dfrac{1}{5}+\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}+\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}< \dfrac{1}{2}\)
Lời giải:
Ta có:
\(\left\{\begin{matrix} \frac{1}{13}< \frac{1}{12}\\ \frac{1}{14}< \frac{1}{12}\\ \frac{1}{15}< \frac{1}{12}\end{matrix}\right.\Rightarrow \frac{1}{13}+\frac{1}{14}+\frac{1}{15}< \frac{3}{12}=\frac{1}{4}(1)\)
\(\left\{\begin{matrix} \frac{1}{61}< \frac{1}{60}\\ \frac{1}{62}< \frac{1}{60}\\ \frac{1}{63}< \frac{1}{60}\end{matrix}\right.\Rightarrow \frac{1}{61}+\frac{1}{62}+\frac{1}{63}< \frac{3}{60}=\frac{1}{20}(2)\)
Từ \((1);(2)\Rightarrow \frac{1}{5}+\frac{1}{13}+\frac{1}{14}+\frac{1}{15}+\frac{1}{61}+\frac{1}{62}+\frac{1}{63}< \frac{1}{5}+\frac{1}{4}+\frac{1}{20}\)
Hay \( \frac{1}{5}+\frac{1}{13}+\frac{1}{14}+\frac{1}{15}+\frac{1}{61}+\frac{1}{62}+\frac{1}{63}< \frac{1}{2}\)
Ta có đpcm.
Đúng 0
Bình luận (0)
Đặt A là biểu thức đó
Ta có:
\(\dfrac{1}{13}< \dfrac{1}{12};\dfrac{1}{14}< \dfrac{1}{12};\dfrac{1}{15}< \dfrac{1}{12}\)
\(\Rightarrow\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}< \dfrac{1}{12}\)
Ta cũng có
\(\dfrac{1}{61}< \dfrac{1}{60};\dfrac{1}{62}< \dfrac{1}{60};\dfrac{1}{63}< \dfrac{1}{60}\)
\(\Rightarrow\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}< \dfrac{1}{60}\)
\(\Rightarrow A< \dfrac{1}{5}+\dfrac{1}{12}.3+\dfrac{1}{60}.3\)
\(\Rightarrow A< \dfrac{1}{5}+\dfrac{1}{4}+\dfrac{1}{20}=\dfrac{1}{2}\)
\(\Rightarrow\)dpcm
Đúng 0
Bình luận (0)
BT2: Tính nhanh
11) \(-\dfrac{5}{7}-\left(-\dfrac{5}{67}\right)+\dfrac{13}{30}+\dfrac{1}{2}+\left(-1\dfrac{5}{6}\right)+1\dfrac{3}{14}-\left(-\dfrac{2}{5}\right)\)
12) \(\dfrac{-1}{4}.13\dfrac{9}{11}-0.25.6\dfrac{2}{11}\)
11: \(=\dfrac{-5}{7}+\dfrac{5}{67}+\dfrac{13}{30}+\dfrac{1}{2}-\dfrac{11}{6}+\dfrac{17}{14}+\dfrac{2}{5}\)
\(=\left(\dfrac{-5}{7}+\dfrac{1}{2}+\dfrac{17}{14}\right)+\left(\dfrac{13}{30}-\dfrac{11}{6}+\dfrac{2}{5}\right)+\dfrac{5}{67}\)
\(=\dfrac{-10+7+17}{14}+\dfrac{13-55+12}{30}+\dfrac{5}{67}\)
\(=1-1+\dfrac{5}{67}=\dfrac{5}{67}\)
12: \(=\dfrac{-1}{4}\cdot\dfrac{152}{11}-\dfrac{1}{4}\cdot\dfrac{68}{11}\)
\(=\dfrac{-1}{4}\left(\dfrac{152}{11}+\dfrac{68}{11}\right)=-\dfrac{1}{4}\cdot20=-5\)
Đúng 0
Bình luận (0)
a)Tìm số nguyên sao cho 4n-5 chia hết cho n-3
b)Chứng minh rằng:
S=\(\dfrac{1}{5}+\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}+\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}< \dfrac{1}{2}\)
a) Giải:
Ta có: \(4n-5=4\left(n-3\right)+7\)
Để \(\left(4n-5\right)⋮\left(n-3\right)\Leftrightarrow7⋮n-3\)
\(\Rightarrow n-3\inƯ\left(7\right)\)
Mà \(Ư\left(7\right)\in\left\{\pm1;\pm7\right\}\)
Nên ta có bảng sau:
| \(n-3\) | \(n\) |
| \(1\) | \(4\) |
| \(-1\) | \(2\) |
| \(-7\) | \(-4\) |
| \(7\) | \(10\) |
Vậy \(n=\left\{2;4;-4;10\right\}\)
b) Ta có:
\(S=\dfrac{1}{5}+\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}+\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}\)
\(=\dfrac{1}{5}+\left(\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}\right)+\left(\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}\right)\)
Nhận xét:
\(\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}< \dfrac{1}{12}+\dfrac{1}{12}+\dfrac{1}{12}=\dfrac{1}{4}\)
\(\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}< \dfrac{1}{60}+\dfrac{1}{60}+\dfrac{1}{60}=\dfrac{1}{20}\)
\(\Rightarrow S< \dfrac{1}{5}+\dfrac{1}{4}+\dfrac{1}{20}=\dfrac{1}{2}\)
Vậy \(S=\dfrac{1}{5}+\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}+\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}\) \(< \dfrac{1}{2}\) (Đpcm)
Đúng 0
Bình luận (0)