Tính số đo các góc
a) sinα = 0,512
b)cotA = 2
c)tanB = 2
Những câu hỏi liên quan
Chứng minh rằng: 1/(tana+tanb) - 1/(Cota+Cotb) = Cot(a+b)
Lời giải:
Sử dụng các công thức sau:
\(\bullet \tan \alpha=\frac{1}{\cot \alpha}\)
\(\bullet \tan (\alpha+\beta)=\frac{\tan \alpha+\tan \beta}{1-\tan\alpha.\tan \beta}\)
Ta có:
\(\text{VT}=\frac{1}{\tan a+\tan b}-\frac{1}{\cot a+\cot b}=\frac{1}{\tan a+\tan b}-\frac{1}{\frac{1}{\tan a}+\frac{1}{\tan b}}\)
\(=\frac{1}{\tan a+\tan b}-\frac{\tan a\tan b}{\tan a+\tan b}=\frac{1-\tan a\tan b}{\tan a+\tan b}\)
\(=\frac{1}{\frac{\tan a+\tan b}{1-\tan a\tan b}}=\frac{1}{\tan (a+b)}=\cot (a+b)=\text{VP}\)
Ta có đpcm.
Đúng 0
Bình luận (1)
cho ABCD là h.thang cân có ^A =2^D . tính số đo các gócA,B,C,D
vẽ đg trung trực d của AB . cm d là đg trung trực của CD
Số đo các góc của tam giác ABC biết 21 gócA=14 gócB=6 gócC.Tính số đo mỗi góc
Dựng góc α, sau đó sử dụng máy tính và thước đo góc để tìm số đo gần đúng của a.
a) sinα = \(\dfrac{1}{3}\)
b) cosα = \(\dfrac{1}{2}\)
c) tanα = 1
d) cotα = 2
Cho tam giác ABC vuông tại C có sinA=3/5 .không tính số đo góc A.Hãy tính cosA,tanA,cotA
\(\sin^2\widehat{A}+\cos^2\widehat{A}=1\Leftrightarrow\cos^2\widehat{A}=1-\left(\dfrac{3}{5}\right)^2=1-\dfrac{9}{25}=\dfrac{16}{25}\\ \Leftrightarrow\cos\widehat{A}=\dfrac{4}{5}\\ \tan\widehat{A}=\dfrac{\sin\widehat{A}}{\cos\widehat{A}}=\dfrac{3}{4}\\ \Rightarrow\cot\widehat{A}=\dfrac{1}{\tan\widehat{A}}=\dfrac{4}{3}\)
Đúng 3
Bình luận (0)
Cho tam giác ABC vuông tại C có sinA=3/5 .không tính số đo góc A.Hãy tính cosA,tanA,cotA.
Cho tam giác ABC vuông tại C có sinA=3/5 .không tính số đo góc A.Hãy tính cosA,tanA,cotA.
cho tam giác ABC có các góc thõa mãn
tanA/2 + tanB/2 <= 2tanC/2
cotA/2 +cotB/2 <= 2cotC/2
CMR: tam giác ABC đều
ML
SGK Kết nối tri thức với cuộc sống - Trang 31
22 tháng 8 2023 lúc 23:35
Dùng thước đo để tìm số đo các góc
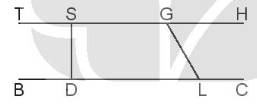
a) Góc đỉnh S; cạnh ST, SD. b) Góc đỉnh D; cạnh DS, DL.
c) Góc đỉnh G; cạnh GS, GL. d) Góc đỉnh L; cạnh LG, LC.
a) Góc đỉnh S; cạnh ST, SD có số đo góc là 90o
b) Góc đỉnh D; cạnh DS, DL có số đo góc là 90o
c) Góc đỉnh G; cạnh GS, GL có số đo góc là 120o
d) Góc đỉnh L; cạnh LG, LC có số đo góc là 120o
Đúng 1
Bình luận (0)
Chứng minh rằng với 0<=a,b<=90 thì
\(\frac{tana+tanb}{2}\ge tan\frac{a+b}{2}\)
\(\frac{cota+cotb}{2}\ge cot\frac{a+b}{2}\)