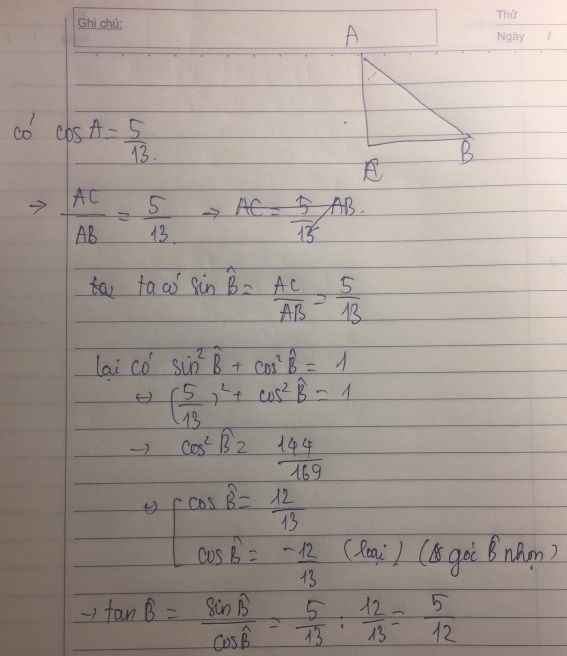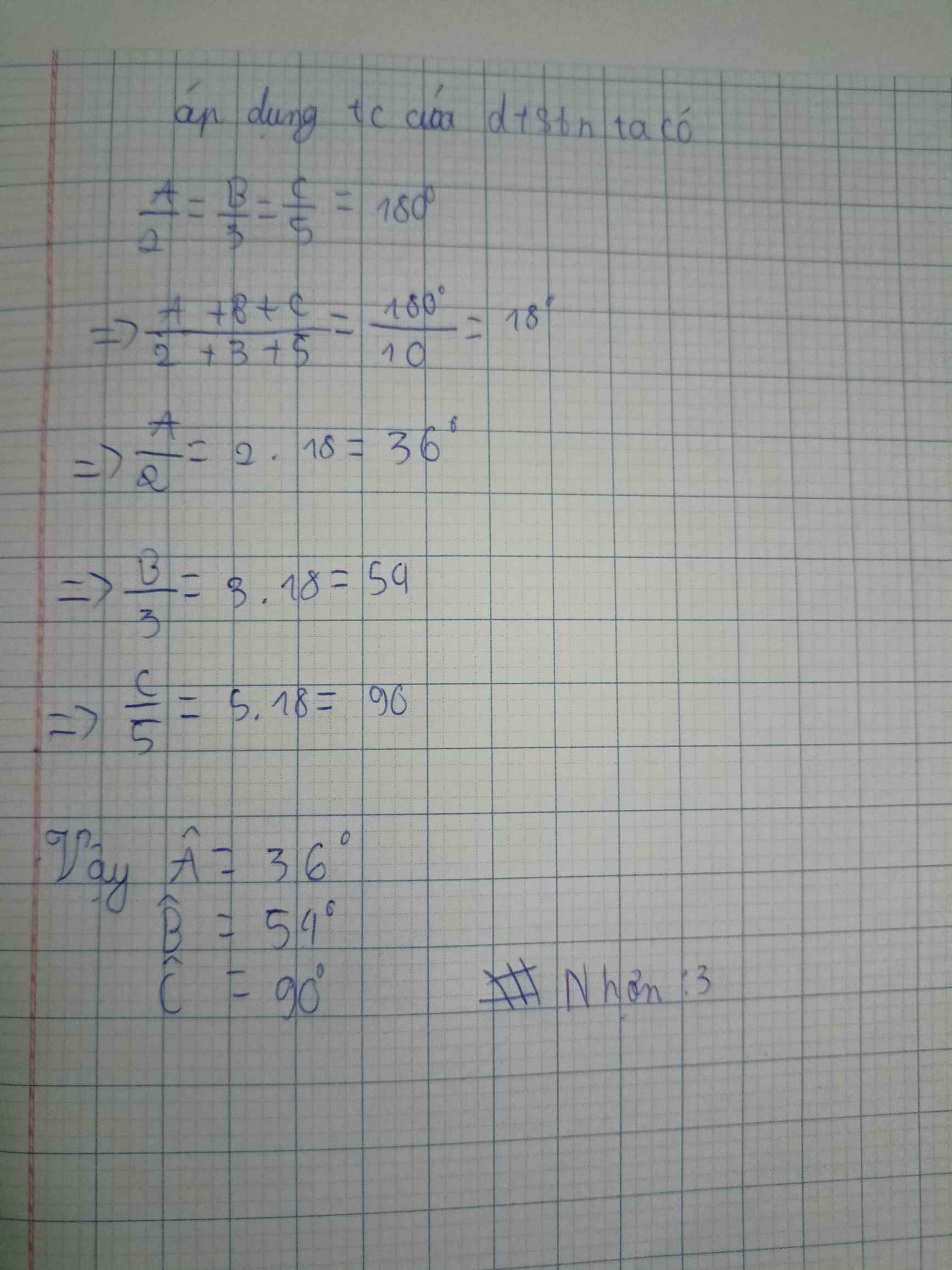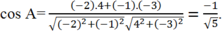1/Cho tam giác ABC có b=7,c=5,cosA=\(\dfrac{3}{5}\).Tính R.\(\dfrac{3}{5}\)

Những câu hỏi liên quan
Cho tam giác ABC có b = 7 ,c = 5 và cos A = \(\dfrac{3}{5}\). Tính a , sin A, diện tích S của ABC, R, r, ha
\(a^2=b^2+c^2-2bc.\cos A\Rightarrow a=\sqrt{b^2+c^2-2bc.cosA}=\sqrt{7^2+5^2-\dfrac{2.7.5.3}{5}}=4\sqrt{2}\)
\(\sin A=\sqrt{1-cos^2A}=\sqrt{1-\left(\dfrac{3}{5}\right)^2}=\dfrac{4}{5}\)
\(p=\dfrac{a+b+c}{2}=6+2\sqrt{2}\)
\(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}=14\)
\(R=\dfrac{a}{2.sinA}=\dfrac{4\sqrt{2}}{\dfrac{2.4}{5}}=\dfrac{5\sqrt{2}}{2}\)
\(r=\dfrac{S}{p}=\dfrac{14}{6+2\sqrt{2}}=3-\sqrt{2}\)
\(ha=\dfrac{2S}{a}=\dfrac{2.14}{4\sqrt{2}}=2\sqrt{2}\)
Đúng 1
Bình luận (0)
\(\cos A=\dfrac{b^2+c^2-a^2}{2bc}\)
\(\Leftrightarrow7^2+5^2-a^2=\dfrac{3}{5}\cdot2\cdot7\cdot5=3\cdot2\cdot7=42\)
\(\Leftrightarrow a^2=32\)
hay \(a=4\sqrt{2}\)
\(\sin A=\sqrt{1-\left(\dfrac{3}{5}\right)^2}=\dfrac{4}{5}\)
Đúng 2
Bình luận (0)
* Cho tam giác ABC vuông tại C. Biết cosA=\(\dfrac{5}{13}\). Tính tan B
\(\sin\widehat{A}=\sqrt{1-\left(\dfrac{5}{13}\right)^2}=\dfrac{12}{13}\)
\(\cot\widehat{A}=\dfrac{5}{13}:\dfrac{12}{13}=\dfrac{5}{12}\)
\(\tan\widehat{B}=\dfrac{5}{12}\)
Đúng 2
Bình luận (0)
Cho tam giác ABC cân tại A với A (2; - 2) , B (-1 ; -2) và C (a;b)Tìm a,b biết cosA = \(\dfrac{3}{5}\)
\(\overrightarrow{BA}=\left(3;0\right)\Rightarrow AB=3=AC\) ; \(\overrightarrow{AC}=\left(a-2;b+2\right)\) ; \(\overrightarrow{BC}=\left(a+1;b+2\right)\)
\(BC=\sqrt{AB^2+AC^2-2AB.AC.cosA}=\dfrac{6\sqrt{5}}{5}\)
\(\Rightarrow\left\{{}\begin{matrix}\left(a-2\right)^2+\left(b+2\right)^2=9\\\left(a+1\right)^2+\left(b+2\right)^2=\dfrac{36}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(a;b\right)=\left(\dfrac{1}{5};-\dfrac{22}{5}\right)\\\left(a;b\right)=\left(\dfrac{1}{5};\dfrac{2}{5}\right)\end{matrix}\right.\)
Đúng 0
Bình luận (1)
Cho tam giác ABC có b 7; c 5, cosA 3/5. Đường cao ha của tam giác ABC là A. B. 6. C. D.
Đọc tiếp
Cho tam giác ABC có b = 7; c = 5, cosA = 3/5. Đường cao ha của tam giác ABC là
A. ![]()
B. 6.
C. ![]()
D. ![]()
Chọn A.
Áp dụng định lí cosin trong tam giác ta có:
a2 = b2 + c2 = 2bc.cosA = 72 + 52 - 2.7.5.3/5 = 32
Nên ![]()
Mặt khác: sin2A + cos2A = 1 nên sin2A = 1 - cos2A = 16/25
Mà sinA > 0 nên sinA = 4/5
Mà: 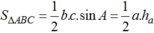
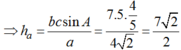
Đúng 1
Bình luận (0)
cho tam giác ABC có b=7, c=5, cosA=\(\dfrac{3}{5}\).tính đường cao \(h_a\) của tam giác ABC
Cho tam giác ABC có
\(\dfrac{A}{2}\)=\(\dfrac{C}{3}\)=\(\dfrac{C}{5}\).Tính số đo mỗi góc
Cho tam giác ABC thỏa mãn:
\(\dfrac{a+b}{6}=\dfrac{b+c}{5}=\dfrac{c+a}{7}\)
Tính cosA, cosB, cosC
Lời giải:
Đặt \(\frac{a+b}{6}=\frac{b+c}{5}=\frac{c+a}{7}=k\Rightarrow \left\{\begin{matrix}
a+b=6k\\
b+c=5k\\
c+a=7k\end{matrix}\right.(1)\)
\(\Rightarrow 2(a+b+c)=6k+5k+7k=18k\Rightarrow a+b+c=9k(2)\)
Từ \((1);(2) \Rightarrow \left\{\begin{matrix} c=3k\\ a=4k\\ b=2k\end{matrix}\right.\)
Theo định lý hàm số cos ta có:
\(a^2=b^2+c^2-2bc\cos A\)
\(\Rightarrow \cos A=\frac{b^2+c^2-a^2}{2bc}=\frac{(2k)^2+(3k)^2-(4k)^2}{2.2k.3k}=\frac{-1}{4}\)
Tương tự: \(\cos B=\frac{c^2+a^2-b^2}{2ac}=\frac{7}{8}\)
\(\cos C=\frac{a^2+b^2-c^2}{2ab}=\frac{11}{16}\)
Đúng 0
Bình luận (0)
Bài 1: a) Thực hiện phép tính: dfrac{17}{13}-dfrac{5}{3} b) Cho tam giác ABC có góc A70o và gócB65o . Tính số đo của góc C.Bài 2: a) Tìm x biết: x+3dfrac{1}{2}dfrac{11}{5}b) Vẽ đồ thị của hàm số y 3xc) Tính nhanh: left(dfrac{-3}{7}+dfrac{5}{11}right):dfrac{4}{31}+left(dfrac{-4}{7}+dfrac{6}{11}right):dfrac{4}{31}
Đọc tiếp
Bài 1:
a) Thực hiện phép tính: \(\dfrac{17}{13}\)-\(\dfrac{5}{3}\)
b) Cho tam giác ABC có góc A=70o và gócB=65o . Tính số đo của góc C.
Bài 2:
a) Tìm x biết: \(x+3\dfrac{1}{2}=\dfrac{11}{5}\)
b) Vẽ đồ thị của hàm số y = 3x
c) Tính nhanh: \(\left(\dfrac{-3}{7}+\dfrac{5}{11}\right):\dfrac{4}{31}+\left(\dfrac{-4}{7}+\dfrac{6}{11}\right):\dfrac{4}{31}\)
B1:
a.(-14/39)
b.45 độ
B2:
a.x=(-13/10)
b.
c.0
Đúng 2
Bình luận (2)
Bài 1:
a/\(\dfrac{17}{3}-\dfrac{5}{3}=\dfrac{17-5}{3}=\dfrac{12}{3}\)=4
b/Tam giác ABC có:
góc A+góc B+góc C=180 độ
=>70 độ+65 độ+góc C=180 độ
=>góc C =180 độ-70 độ-65 độ=45 độ
Bài 2:
a/\(x+3\dfrac{1}{2}=\dfrac{11}{5}=>x+\dfrac{7}{2}=\dfrac{11}{5}=>x=\dfrac{11}{5}-\dfrac{7}{2}=\dfrac{-13}{10}\)
c/\(\left(\dfrac{-3}{7}+\dfrac{5}{11}\right):\dfrac{4}{31}+\left(\dfrac{-4}{7}+\dfrac{6}{11}\right):\dfrac{4}{31}\)
=>\(\left(\dfrac{-3}{7}+\dfrac{5}{11}\right).\dfrac{31}{4}+\left(\dfrac{-4}{7}+\dfrac{6}{11}\right).\dfrac{31}{4}\)
=>\(\dfrac{31}{4}.\left(\dfrac{-3}{7}+\dfrac{5}{11}+\dfrac{\left(-4\right)}{7}+\dfrac{6}{11}\right)=\dfrac{31}{4}.0=0\)
Đúng 1
Bình luận (1)
Cho tam giác ABC có A(1; 2); B(-1; 1) và C(5; -1).Tính cosA.
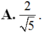
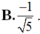
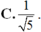
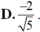
Cho tam giác ABC có ba cạnh a,b,c. Chứng minh rằng:
\(\dfrac{a^2+b^2+c^2}{2abc}=\dfrac{cosA}{a}+\dfrac{cosB}{b}+\dfrac{cosC}{c}\)
\(\dfrac{cosA}{a}+\dfrac{cosB}{b}+\dfrac{cosC}{c}\)
\(=\dfrac{b^2+c^2-a^2}{2abc}+\dfrac{a^2+c^2-b^2}{2abc}+\dfrac{a^2+b^2-c^2}{2abc}\)
\(=\dfrac{a^2+b^2+c^2}{2abc}\) (đpcm)
Đúng 1
Bình luận (0)
a2 = b2 + c2 - 2bc.cosA
b2 = a2 + c2 - 2ac.cosB
c2 = a2 + b2 - 2ab.cosC
⇒ a2 + b2 + c2 = 2bc.cosA + 2ac.cosB + 2ab.cosC
⇒ VT = \(\dfrac{2bc.cosA}{2abc}+\dfrac{2ab.cosC}{2abc}+\dfrac{2ac.cosB}{2abc}\)
⇒ VT = \(\dfrac{cosA}{a}+\dfrac{cosB}{b}+\dfrac{cosC}{c}\)
Đúng 0
Bình luận (0)