Lời giải:

$A=1+\frac{1}{\sqrt{x}-3}$

Để $A$ max thì $\sqrt{x}-3$ phải dương và nhỏ nhất. 

Với $x$ nguyên, để $\sqrt{x}-3$ dương và nhỏ nhất thì $x=10$

Khi đó, $A_{\max}=1+\frac{1}{\sqrt{10}-3}=4+\sqrt{10}$

------------------

$B=1+\frac{1}{\sqrt{x}-2}$.

Lập luận tương tự phần a, ta thấy với $x$ nguyên không âm thì $\sqrt{x}-2$ đạt giá trị dương nhỏ nhất tại $x=5$

$\Rightarrow B_{\max}=1+\frac{1}{\sqrt{5}-2}=3+\sqrt{5}$

\(\dfrac{n}{2n-1}>\dfrac{n}{2n}=\dfrac{1}{2}\)

\(\Rightarrow x_{n+1}>\dfrac{1}{2}.\left(\dfrac{x_n^2+2}{x_n}\right)\ge\dfrac{1}{2}.\dfrac{2\sqrt{2x_n^2}}{x_n}=\sqrt{2}\)

Dãy bị chặn dưới bởi \(\sqrt{2}\)

Ta sẽ chứng minh dãy đã cho là dãy giảm, hay \(x_{n+1}-x_n< 0\) với \(n>1\)

\(\Leftrightarrow\dfrac{n}{2n-1}\left(\dfrac{x_n^2+2}{x_n}\right)-x_n< 0\Leftrightarrow\left(1-n\right)x_n^2+2n< 0\)

\(\Leftrightarrow x_n^2>\dfrac{2n}{n-1}\Leftrightarrow x_n>\sqrt{\dfrac{2n}{n-1}}\)

Do \(x_n=\dfrac{n-1}{2\left(n-1\right)-1}.\left(\dfrac{x_{n-1}^2+2}{x_{n-1}}\right)=\dfrac{n-1}{2n-3}.\left(\dfrac{x_{n-1}^2+2}{x_{n-1}}\right)\ge\dfrac{2\sqrt{2}\left(n-1\right)}{2n-3}\)

Nên ta chỉ cần chứng minh: \(\dfrac{2\sqrt{2}\left(n-1\right)}{2n-3}>\sqrt{\dfrac{2n}{n-1}}\)

\(\Leftrightarrow6n-8>0\) (đúng)

Vậy dãy đã cho là dãy giảm

Dãy giảm và bị chặn dưới nên có giới hạn

Gọi giới hạn của dãy là L, lấy giới hạn 2 vế biểu thức truy hồi:

\(\lim\left(x_{n+1}\right)=\lim\left(\dfrac{n}{2n-1}.\dfrac{x_n^2+2}{x_n}\right)\Rightarrow L=\dfrac{1}{2}\left(\dfrac{L^2+2}{L}\right)\)

\(\Rightarrow L^2=2\Rightarrow L=\sqrt{2}\)

a.

\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{4+x}-2}{4x}=\lim\limits_{x\rightarrow0}\dfrac{\left(\sqrt{4+x}-2\right)\left(\sqrt{4+x}+2\right)}{4x\left(\sqrt{4+x}+2\right)}\)

\(=\lim\limits_{x\rightarrow0}\dfrac{x}{4x\left(\sqrt{4+x}+2\right)}=\lim\limits_{x\rightarrow0}\dfrac{1}{4\left(\sqrt{4+x}+2\right)}=\dfrac{1}{4\left(\sqrt{4+0}+2\right)}=\dfrac{1}{16}\)

b.

\(\lim\limits_{x\rightarrow1}\dfrac{\sqrt[3]{x+7}-2}{x-1}=\lim\limits_{x\rightarrow1}\dfrac{\left(\sqrt[3]{x+7}-2\right)\left(\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4\right)}{\left(x-1\right)\left(\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4\right)}\)

\(=\lim\limits_{x\rightarrow1}\dfrac{x-1}{\left(x-1\right)\left(\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4\right)}=\lim\limits_{x\rightarrow1}\dfrac{1}{\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4}\)

\(=\dfrac{1}{\sqrt[3]{8^2}+2\sqrt[3]{8}+4}=\dfrac{1}{12}\)

D

C

ủa vậy đáp án nào ạ??

\(x+y=1\Rightarrow x=1-y\) 

\(C=x^2+y^2+xy=\left(1-y\right)^2+y^2+\left(1-y\right)y\)

\(=y^2-y+1\)\(=\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall y\)

=>minC=\(\dfrac{3}{4}\) \(\Leftrightarrow y=\dfrac{1}{2}\Rightarrow x=\dfrac{1}{2}\)

Ta có :

\(x+y=1\Rightarrow\left(x+y\right)^2=1\)

\(\Leftrightarrow x^2+2xy+y^2=1\)

\(\Leftrightarrow x^2+xy+y^2=1-xy\ge1-\left(\dfrac{x+y}{2}\right)^2=1-\dfrac{1}{4}=\dfrac{3}{4}\)

Hay \(C \ge \dfrac{3}{4}\)

Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)

6.4

\(y=\dfrac{3}{2}\left(1+cos2x\right)-\sqrt{3}sin2x+\dfrac{1}{2}-\dfrac{1}{2}cos2x\)

\(=cos2x-\sqrt{3}sin2x+2\)

\(=2\left(\dfrac{1}{2}cos2x-\dfrac{\sqrt{3}}{2}sin2x\right)+2\)

\(=2cos\left(2x-\dfrac{\pi}{3}\right)+2\)

Do \(-1\le cos\left(2x-\dfrac{\pi}{3}\right)\le1\)

\(\Rightarrow0\le y\le4\)

\(y_{min}=0\) khi \(cos\left(2x-\dfrac{\pi}{3}\right)=-1\)

\(y_{max}=4\) khi \(cos\left(2x-\dfrac{\pi}{3}\right)=1\)

6.5

Ủa nhìn bài 7 thì đây là chương trình lớp 11 (pt lượng giác) chứ đâu phải lớp 10?

Vậy giải theo kiểu lớp 11 nghe:

\(y=\dfrac{2+cosx+3sinx}{2+cosx}\)

\(\Leftrightarrow2y+y.cosx=2+cosx+3sinx\)

\(\Leftrightarrow3sinx+\left(1-y\right).cosx=2y-2\)

Theo điều kiện có nghiệm của pt lượng giác bậc nhất:

\(9+\left(1-y\right)^2\ge\left(2y-2\right)^2\)

\(\Leftrightarrow\left(y-1\right)^2\le3\)

\(\Rightarrow1-\sqrt{3}\le y\le1+\sqrt{3}\)

7.

\(\Leftrightarrow\left(m+1\right)\left[\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)\right]+cos4x=0\)

\(\Leftrightarrow\left(m+1\right)\left(1-3sin^2x.cos^2x\right)+cos4x=0\)

\(\Leftrightarrow\left(m+1\right)\left(1-\dfrac{3}{4}sin^22x\right)+cos4x=0\)

\(\Leftrightarrow\left(m+1\right)\left(1-\dfrac{3}{8}\left(1-cos4x\right)\right)+cos4x=0\)

\(\Leftrightarrow\left(m+1\right)\left(\dfrac{5}{8}+\dfrac{3}{8}cos4x\right)+cos4x=0\)

\(\Leftrightarrow5\left(m+1\right)+\left(3m+11\right)cos4x=0\)

\(\Leftrightarrow\left(3m+11\right)cos4x=-5\left(m+1\right)\)

- Với \(m=-\dfrac{11}{3}\) pt vô nghiệm

- Với \(m\ne-\dfrac{11}{3}\)

\(\Rightarrow cos4x=\dfrac{-5\left(5m+1\right)}{3m+11}\)

Do \(-1\le cos4x\le1\) nên pt có nghiệm khi:

\(-1\le\dfrac{-5\left(m+1\right)}{3m+11}\le1\)

Tới đây chắc bạn tự làm tiếp được đúng ko? Tách ra làm 2 BPT rồi sau đó giao nghiệm thôi

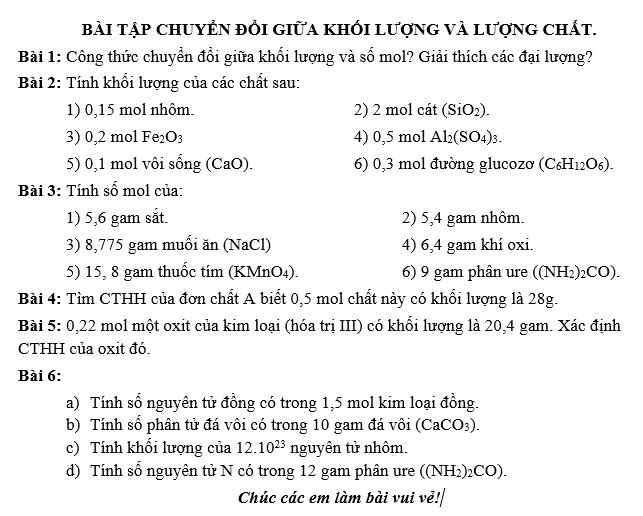
Bài 5:

Gọi kim loại đó là R thì CTHH oxit KL đó là \(R_2O_3\)

\(M_{R_2O_3}=\dfrac{20,4}{0,22}\approx102(g/mol)\\ \Rightarrow M_R=\dfrac{102-3.16}{2}=27(g/mol)\\ \text {Vậy R là nhôm (Al) và CTHH oxit là }Al_2O_3\)

Bài 6:

\(a,1,5.6.10^{-23}=9.10^{-23}(\text {nguyên tử Cu})\\ b,n_{CaCO_3}=\dfrac{10}{100}=0,1(mol)\\ \text {Số phân tử đá vôi là: }0,1.6.10^{-23}=0,6.10^{-23}\\ c,n_{Al}=\dfrac{12.10^{-23}}{6.10^{-23}}=2(mol)\\ \Rightarrow m_{Al}=2.27=54(g)\\ d,\%_N=\dfrac{14.2}{60}.100\%=\dfrac{140}{3}\%\\ \Rightarrow m_{N}=12.\dfrac{140}{3}\%=5,6(g)\\ \Rightarrow n_{N}=\dfrac{5,6}{14}=0,4(mol)\\ \text {Số nguyên tử N là: }0,4.6.10^{-23}=2,4.10^{-23}\)

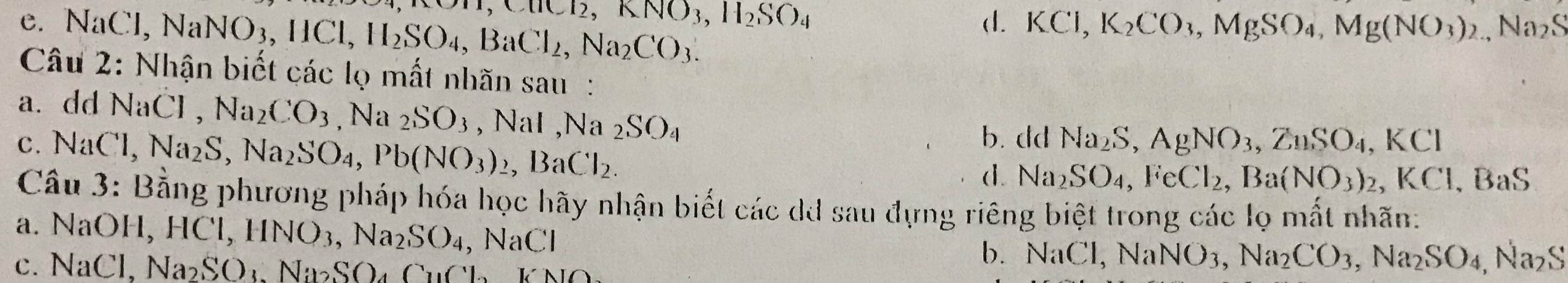
Bài 2:

- Trích một ít các chất làm mẫu thử

a)

- Cho các dd tác dụng với dd BaCl₂

+ Kết tủa trắng: Na₂CO₃, Na₂SO₃, Na₂SO₄ (1)

\(Na_2CO_3+BaCl_2\rightarrow2NaCl+BaCO_3\downarrow\)

\(Na_2SO_3+BaCl_2\rightarrow BaSO_3\downarrow+2NaCl\)

\(Na_2SO_4+BaCl_2\rightarrow BaSO_4\downarrow+2NaCl\)

+ Không hiện tượng: NaCl, NaI (2)

- Cho các chất ở (1) tác dụng với dd HCl dư

+ Có khí không mùi thoát ra: Na₂CO₃

\(Na_2CO_3+2HCl\rightarrow2NaCl+CO_2+H_2O\)

+ Có khí mùi hắc thoát ra: Na₂SO₃

\(Na_2SO_3+2HCl\rightarrow2NaCl+SO_2+H_2O\)

+ Không hiện tượng: Na₂SO₄

- Cho dd ở (2) tác dụng với dd AgNO₃

+ Kết tủa trắng: NaCl

\(NaCl+AgNO_3\rightarrow AgCl\downarrow+NaNO_3\)

+ Kết tủa vàng: NaI

\(NaI+AgNO_3\rightarrow AgI\downarrow+NaNO_3\)

b) 

- Cho các dd tác dụng với dd HCl dư

+ Có khí mùi trứng thối thoát ra: Na₂S

\(Na_2S+2HCl\rightarrow2NaCl+H_2S\)

+ Kết tủa trắng: AgNO₃

\(AgNO_3+HCl\rightarrow AgCl\downarrow+HNO_3\)

+ Không hiện tượng: ZnSO₄, KCl (1)

- Cho dd ở (1) tác dụng với dd BaCl₂

+ Không hiện tượng: KCl

+ Kết tủa trắng: ZnSO₄

\(ZnSO_4+BaCl_2\rightarrow BaSO_4\downarrow+ZnCl_2\)

c) 

- Cho các dd tác dụng với dd H₂SO₄ dư:

+ Không hiện tượng: NaCl, Na₂SO₄ (1)

+ Có khí mùi trứng thối thoát ra: Na₂S

\(Na_2S+H_2SO_4\rightarrow Na_2SO_4+H_2S\)

+ Kết tủa trắng: Pb(NO₃)₂, BaCl₂ (2)

- Cho dd ở (1) tác dụng với dd Ba(NO₃)₂:

+ Không hiện tượng: NaCl

+ Kết tủa trắng: Na₂SO₄

\(Na_2SO_4+Ba\left(NO_3\right)_2\rightarrow BaSO_4\downarrow+2NaNO_3\)

- Cho dd ở (2) tác dụng với dd NaI:

+ Không hiện tượng: BaCl₂

+ Kết tủa vàng: Pb(NO₃)₂

\(Pb\left(NO_3\right)_2+2NaI\rightarrow PbI_2\downarrow+2NaNO_3\)

d)

- Cho các dd tác dụng với dd HCl dư:

+ Có khí mùi trứng thối thoát ra: BaS

\(BaS+2HCl\rightarrow BaCl_2+H_2S\uparrow\)

+ Không hiện tượng: Na₂SO₄, FeCl₂, Ba(NO₃)₂, KCl (1)

- Cho dd ở (1) tác dụng với dd Ba(OH)₂

+ Không hiện tượng: Ba(NO₃)₂, KCl (2)

+ Kết tủa trắng: Na₂SO₄

\(Na_2SO_4+Ba\left(OH\right)_2\rightarrow2NaOH+BaSO_4\downarrow\)

+ Kết tủa trắng xanh: FeCl₂

\(FeCl_2+Ba\left(OH\right)_2\rightarrow BaCl_2+Fe\left(OH\right)_2\downarrow\)

- Cho dd ở (2) tác dụng với dd AgNO₃

+ Không hiện tượng: Ba(NO₃)₂

+ Kết tủa trắng: KCl

\(KCl+AgNO_3\rightarrow AgCl\downarrow+KNO_3\)

\(n_{Fe}=\dfrac{5,6}{56}=0,1\left(mol\right)\\ n_S=\dfrac{0,8}{32}=0,025\left(mol\right)\)

PTHH: Fe + S --to--> FeS

LTL: \(0,1>0,025\rightarrow\) Fe dư

Theo pthh: \(n_{Fe\left(pu\right)}=n_{FeS}=n_S=0,025\left(mol\right)\)

\(\rightarrow\left\{{}\begin{matrix}m_{Fe\left(du\right)}=\left(0,1-0,025\right).56=4,2\left(g\right)\\m_{FeS}=0,025.88=2,2\left(g\right)\end{matrix}\right.\)

PTHH:

Fe + 2HCl ---> FeCl₂ + H₂

0,075                          0,075

FeS + 2HCl ---> FeCl₂ + H₂S

0,025                             0,025

\(\rightarrow\left\{{}\begin{matrix}\%V_{H_2}=\dfrac{0,075}{0,075+0,025}=75\%\\\%V_{H_2S}=100\%-75\%=25\%\end{matrix}\right.\)