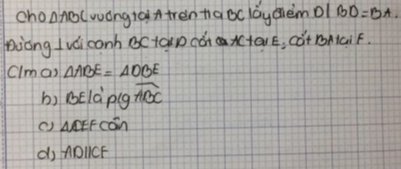 c, tam giác CEF cân nha mn
c, tam giác CEF cân nha mn
giúp mik bài trên với
AD
Những câu hỏi liên quan
cho tam giác ABC cân tại A.kẻ AH vuông góc BC tại H.kẻ HM vuông góc AB và HN vuông góc AC chứng minh
a)tam giác BMH =tam giác CNH
b)tam giác AMN cân
c)AH vuông góc MN
giúp mik vs please 🥺🥺🥺
a: Xét ΔBMH vuông tại M và ΔCNH vuông tại N có
BH=CH
\(\widehat{B}=\widehat{C}\)
Do đó: ΔBMH=ΔCNH
b: Ta có: ΔBMH=ΔCNH
nên BM=CN
=>AM=AN
hay ΔAMN cân tại A
c: Xét ΔABC có AM/AB=AN/AC
nên MN//BC
mà AH⊥BC
nên AH⊥MN
Đúng 1
Bình luận (1)
Cho tam giác ABC cân tại A. Trên tia đối của AB và AC, kẻ D và E sao cho BD = CE a) chứng minh tam giác ADE cân, DE//BC b) Từ D kẻ DM vuông góc với BC, từ E kẻ EN vuông góc với BC. Cm DM=EN c) chứng minh tam giác AMN là tam giác cân ( giải hộ mik nhanh nha)
a, Ta có : AD = AB + BD ; AE = AC + CE
mà AB = AC (gt); BD = CE (gt)
=> AD = AE
Vậy tam giác ADE cân tại A
Ta có : \(\dfrac{AB}{AD}=\dfrac{AC}{AE}\)do AB = AC; AD = AE(cmt)
=> DE // BC ( Ta lét đảo )
b, Vì ^ABC = ^MDB ( đối đỉnh )
^ACB = ^NCE ( đối đỉnh )
mà ^ABC = ^ACB ( tam giác ABC cân tại A )
=> ^MDB = ^NCE
Xét tam giác DMB và tam giác ENC có :
BD = EC (cmt)
^MDB = ^NCE ( cmt )
Vậy tam giác DMB = tam giác ENC ( ch - gn )
=> DM = EN ( 2 cạnh tương ứng )
=> BM = NC ( 2 cạnh tương ứng )
c, Ta có : ^ABM = ^MBC - ^ABC
^ACN = ^NCM = ^ACB
=> ^ABM = ^ACN
Xét tam giác ABM và tam giác ACN có :
AB = AC (gt)
^ABM = ^ACN (cmt)
BM = CN (cmt)
Vậy tam giác ABM = tam giác ACN ( c.g.c )
=> ^AMB = ^ANC ( 2 góc tương ứng )
Xét tam giác AMN có : ^AMB = ^ANC (cmt)
Vậy tam giác AMN cân tại A
Đúng 1
Bình luận (0)
Bạn vẽ hình giúp mình nha
a. Tam giác ABC cân tại A nên AB=AC
Ta có: AE=AC+CE, AD=AB+BD
Mà AC=AB, CE=BD
\(\Rightarrow AE=AD\) \(\Rightarrow\Delta ADE\) cân tại A
Xét \(\Delta ADE\) có: \(\dfrac{AB}{BD}=\dfrac{AC}{CE}\)
Áp dụng định lí Ta-let đảo \(\Rightarrow BC//DE\) (đpcm)
Xét \(\Delta BDM\) vuông tại M và \(\Delta CEN\) vuông tại N có:
\(\left\{{}\begin{matrix}BD=CE\\\widehat{MBD}=\widehat{NEC}\left(cùng.bằng.\widehat{ABC}\right)\end{matrix}\right.\)
\(\Rightarrow\)\(\Delta BDM\)=\(\Delta CEN\) \(\Rightarrow\)DM=EN (đpcm)
Kẻ \(AH\perp BC\) \(\left(H\in BC\right)\)
Ta có \(\Delta ABC\) cân tại A nên AH vừa là đường cao vừa là đường trung tuyến
\(\Rightarrow BH=CH\)
Mà MB=CN (\(\Delta BDM\)=\(\Delta CEN\)) \(\Rightarrow AM=AN\)
\(\Rightarrow\Delta AMN\) cân tại A
Đúng 1
Bình luận (0)
cho tam giác ABC vuông cân tại A. Tia pg góc A cắt BC tại D, lấy điểm E trên cạnh AB, F trên cạnh AC sao cho AE=CF
CMR:a) tam giác ACB, tam giác ADC là tam giác vuông cân
b) tam giác CEF vuông cân
Cho tam giác ABC, trên hai cạnh AB, AC lấy hai điểm D và E sao cho
BD = CE. Gọi M là trung điểm DE. Trên tia đối của tia MB lấy điểm F sao cho MF = MB
a, Chứng minh tam giác MDB = tam giác MEF
b, Chứng minh tam giác CEF cân
c, Kẻ phân giác AK của góc BAC. Chứng minh AK // CF
B19
a: Xét ΔMDB và ΔMEF có
MD=ME
góc DMB=góc EMF
MB=MF
=>ΔMDB=ΔMEF
b: ΔMDB=ΔMEF
=>DB=EF
=>EC=EF
=>ΔECF cân tại E
Đúng 0
Bình luận (0)
Cho tam giác ABC, trên hai cạnh AB, AC lấy hai điểm D và E sao cho
BD = CE. Gọi M là trung điểm DE. Trên tia đối của tia MB lấy điểm F sao cho MF = MB
a, Chứng minh tam giác MDB = tam giác MEF
b, Chứng minh tam giác CEF cân
c, Kẻ phân giác AK của góc BAC. Chứng minh AK // CF
a: Xét ΔMDB và ΔMEF có
MD=ME
góc DMB=góc EMF
MB=MF
=>ΔMDB=ΔMEF
b: ΔMDB=ΔMEF
=>DB=EF
=>EC=EF
=>ΔECF cân tại E
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Trên tia BC lấy điểm D sao cho BD=BA. Đường thẳng vuông góc với cạnh BC tại d cắt AC tại E. Cắt BA tại F. Chứng Minh
a) tam giác ABE = DBE
b)tam giác CEF là tam giác cân
c)AD song song CF
cho tam giác ABC ,trên hai cạnh AB,AC lấy hai điểm D và E sao cho BD = CE .gọi M là trung điểm của DE trên tia đối của tia MB lấy điểm F sao cho MF = MB .
a, chứng minh tam giác MDB =tam giác MEF.
b, chứng minh tam giác CEF cân .
c,kẻ phân giác AK của góc BAC . chứng minh AK song song CF
Cho tam giác ABC ( AB < AC) có AM là phân giác của góc A ( M thuộc BC). Trên AC lấy D sao cho BM = MD
a) C/m: BM = MD
b) Gọi K là giao điểm của AB và DM. C/m: tam giác DAK = tam giác BAC
c) C/m: Tam giác AKC cân
d) So sánh BM và CM
Giúp mik làm bài với nha cần gấp lắm ai làm nhanh nhất và đúng cho sao+ likeeeee
11) Cho tam giác ABC cân tại A, lấy D trên cạnh BA, lấy E trên tia đối của tia CA sao cho CEBD. Từ E vẽ tia song song với AB cắt BC tại Fa) C/m tam giác CEF cânb) Đường DE cắt Bc tại I, C/m I là trung điểm DEtks nhìu mí ngừ lm bài giúp nga
Đọc tiếp
11) Cho tam giác ABC cân tại A, lấy D trên cạnh BA, lấy E trên tia đối của tia CA sao cho CE=BD. Từ E vẽ tia song song với AB cắt BC tại F
a) C/m tam giác CEF cân
b) Đường DE cắt Bc tại I, C/m I là trung điểm DE
tks nhìu mí ngừ lm bài giúp nga![]()
![]()
cho hình tam giác ABC.Trên cạnh AB lấy điểm M sao cho AM = 1/3 AB. Nối C với M,trên cạnh CM lấy trung điểm N.Nối A với N;N với B.Tính diện tích hình tam giác ANB,biết diện tích tam giác ABC là 80cm2
Giúp mik nha,mik cần bài này gấp(vì tối mik phải ik học thêm nhà cô giáo rùi T_T)
mọi người vẽ hình hộ mik hình vẽ nha,mik ko bt vẽ
Hai tg AMC và tg ABC có chung đường cao từ C->AB nên
\(\dfrac{S_{AMC}}{S_{ABC}}=\dfrac{AM}{AB}=\dfrac{1}{3}\Rightarrow S_{AMC}=\dfrac{1}{3}xS_{ABC}\)
Hai tg AMN và tg AMC có chung đường cao từ A->CM nên
\(\dfrac{S_{AMN}}{S_{AMC}}=\dfrac{MN}{MC}=\dfrac{1}{2}\Rightarrow S_{AMN}=\dfrac{1}{2}xS_{AMC}=\dfrac{1}{2}x\dfrac{1}{3}xS_{ABC}=\dfrac{1}{6}xS_{ABC}\)
\(S_{BMC}=S_{ABC}-S_{AMC}=S_{ABC}-\dfrac{1}{3}xS_{ABC}=\dfrac{2}{3}xS_{ABC}\)
Hai tg BMN và tg BMC có chung đường cao từ B->MC nên
\(\dfrac{S_{BMN}}{S_{BMC}}=\dfrac{MN}{MC}=\dfrac{1}{2}\Rightarrow S_{BMN}=\dfrac{1}{2}xS_{BMC}=\dfrac{1}{2}x\dfrac{2}{3}xS_{ABC}=\dfrac{1}{3}xS_{ABC}\)
\(S_{ANB}=S_{AMN}+S_{BMN}=\dfrac{1}{6}xS_{ABC}+\dfrac{1}{3}xS_{ABC}=\dfrac{1}{2}xS_{ABC}=40cm^2\)
Đúng 3
Bình luận (0)





