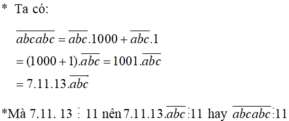Chứng tỏ rằng số có dạng abcabc bao giờ cũng chia hết cho 11(chẳng hạn 328328 chia hết cho 11)
H24
Những câu hỏi liên quan
Chứng tỏ rằng số có dạng (abcabc) bao giờ cũng chia hết cho 11 ( chẳng hạn 328328 ⋮11)
chứng tỏ rằng số có dạng abcabc bao giờ cũng chia hết cho 11(chẳng hạn: 328328 chia hết cho 11)
abc abc=abc.1000+abc=abc.(1000+1)
=abc.1001=abc.91.11
vì 11 chia hết cho 11=>abc.91.11 chia hết cho 11
vậy số abcabc lúc nào cũng chia hết cho 11
Đúng 0
Bình luận (0)
Chứng tỏ rằng số có dạng abcabc bao giờ cũng chia hết cho 11(chẳng hạn 328328 chia hết cho 11)
Theo bài ra ta có :
\(\overline{abcabc}\)
\(=\overline{abc}.1000+\overline{abc}.1\)
\(=\overline{abc}.\left(1000+1\right)\)
\(=\overline{abc}.1001\)
\(=\overline{abc}.11.91\)
\(=\left(\overline{abc}.91\right).11\)
\(\Rightarrow\overline{abcabc}⋮11\left(đpcm\right)\)
Đúng 0
Bình luận (0)
Ta có:
\(\overline{abcabc}=1001\overline{abc}=11.91\overline{abc}\)
Vì \(11.91\overline{abc}\) \(⋮\) 11 nên \(\overline{abcabc}\) \(⋮\) 11
\(\Rightarrow\) ĐPCM(điều phải chứng minh)
Đúng 0
Bình luận (0)
abcabc \(⋮\) 11 vì:
abcabc = abc . 1000 + abc
abcabc = abc . ( 1000 + 1 )
abcabc = abc . 1001
abcabc = abc . 11 . 91
Mà 11 \(⋮\) 11 \(\Rightarrow\) abc . 11 . 91 \(⋮\) 11
Vậy abcabc \(⋮\) 11 ( đpcm )
Đúng 0
Bình luận (0)
Chứng tỏ rằng số có dạng abcabc bao giờ cũng chia hết cho 11 ( chẳng hạn số 328328 chia hết cho 11 )
Ta có:
\(\overline{abcabc}=1001\overline{abc}=11.99\overline{abc}\)
Vì \(11.99\overline{abc}\) \(⋮\) 11 nên \(\overline{abcabc}\) \(⋮\) 11
\(\Rightarrow\text{Điều phải chứng minh}\)
Đúng 0
Bình luận (0)
Vì x ⋮ 11 <=> (a0+a2+a4+...) - (a1+a3+a5+...) ⋮ 11
=> (c+a+b) - (b+c+a) = 0 ⋮ 11
Vậy dạng abcabc bao giờ cũng chia hết cho 11.
Đúng 0
Bình luận (0)
abcabc=a.100000+b.10000+c.1000+a.100+b.10+c.1
=a.100100+b.10010+c.1001
=a00.1001+b0.1001+c.1001
=abc.1001
=(abc.91).11 chia hết cho 11
=> abcabc chia hết cho 11
Đúng 0
Bình luận (0)
chứng tỏ rằng số có dạng abcabc bao giờ cũng chia hết cho 11(chẳng hạn: 328328 chia hết cho 11)
abc abc=abc.1000+abc=abc.(1000+1)
=abc.1001=abc.91.11
vì 11 chia hết cho 11=>abc.91.11 chia hết cho 11
vậy số abcabc lúc nào cũng chia hết cho 11
Đúng 0
Bình luận (0)
ta co abcabc=1000.abc+abc=abc.1001=91.11.abc
ta co 11 chia hết cho 11 nên abcabc chia hêt cho 11
Đúng 0
Bình luận (0)
ta co abcabc = abc . 1001 = 91.11
vì 11 chia hết cho 11 nên abcabc chia hết cho 11
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng tỏ rằng số có dạng abcabc bao giờ cũng chia hết cho 11 (chẳng hạn 328328 chia hết cho 11)
Có abcabc = abc . 1000 + abc
abcabc = abc . ( 1000 + 1 )
abcabc = abc . 1001
abcabc = abc . 11 . 91
Mà 11 \(⋮\)11 nên abc . 11 . 91 \(⋮\) 11
Vậy abcabc \(⋮\) 11 ( đpcm )
Đúng 0
Bình luận (0)
Chứng tỏ rằng số có dạng abcabc bao giờ cũng chia hết cho 11( chẳng hạn 328328 chia hết cho 11 )
chứng tỏ rằng số có dạng abcabc bao giờ cũng chia hết cho 11 ( chẳng hạn : 328328 chia hết cho 11 )
abc abc=abc.1000+abc=abc.(1000+1)
=abc.1001=abc.91.11
vì 11 chia hết cho 11=>abc.91.11 chia hết cho 11
vậy số abcabc lúc nào cũng chia hết cho 11
chứng tỏ rằng số có dạng abcabc bao giờ cũng chia hết cho 11 ( chẳng hạn : 328328 chia hết cho 11 ) - Tìm với Google
Đúng 0
Bình luận (0)
Ta có:
abcabc=abc*1001
Mà 1001 chia hết cho 11 và abcEN
=>abc*1001 chia hết cho 11
Vậy........
Đúng 0
Bình luận (0)
Chứng tỏ rằng số có dạng \(\overline{abcabc}\) bao giờ cũng chia hết cho 11 (chẳng hạn \(328328⋮11\)) ?
Ta có : \(\overline{abcabc}=\overline{abc}.1001=\overline{abc}.11.91⋮11\)
\(\Rightarrow\overline{abcabc}⋮11\)
Đúng 0
Bình luận (0)
Ta có \(\overline{abcabc}=\overline{abc}.1001\)
\(=\overline{abc}.11.91⋮11\)
\(=>\overline{abcabc}⋮11\left(dpcm\right)\)
Đúng 0
Bình luận (0)