Chứng minh BĐT sau:
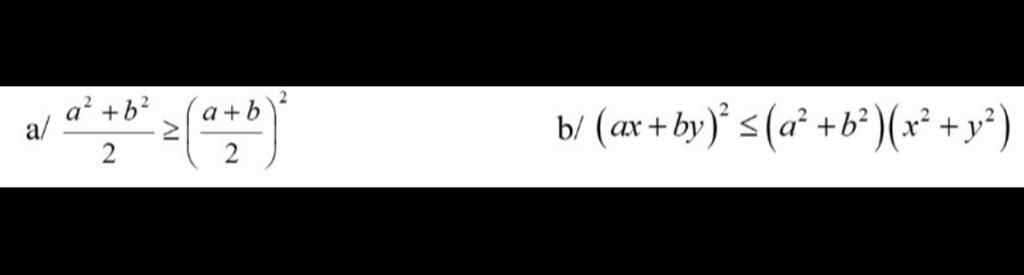
Chứng minh BĐT sau luôn đúng: x > 0
x + \(\dfrac{4}{x}\) \(\ge\) 4
Áp dụng BĐT Cô si ta có: x > 0 => x + \(\dfrac{4}{x}\) \(\ge\) 2 . \(\sqrt{\dfrac{4x}{x}}\)
<=> x + \(\dfrac{4}{x}\) \(\ge\) 4
Ta có: \(x+\dfrac{4}{x}\ge4\)
\(\Leftrightarrow\dfrac{x^2+4}{x}-\dfrac{4x}{x}\ge0\)
\(\Leftrightarrow x^2-4x+4\ge0\forall x\)
\(\Leftrightarrow\left(x-2\right)^2\ge0\forall x>0\)(luôn đúng)
`x+4/x>=4`
`<=>x-4+4/x>=0`
`<=>(sqrtx)^2-2.sqrtx. 2/sqrtx+(2/sqrtx)^2>=0(x>0)`
`<=>(sqrtx-2/sqrtx)^2>=0`(luôn đúng)
`=>` đpcm
Dấu "=" `<=>x=2`
Chứng minh BĐT sau: \(a^2+b^2+1\ge ab+a+b\)
BĐT <=> 2(a2+b2+1) >= 2(ab+a+b)
<=> (a-b)2 + (a-1)2 + (b-1)2 >=0. dpcm
Vào thi tuyển 10 có được sử dụng các dạng BĐT như BĐT Cô-si ko? (có cần phải chứng minh ko)
TL:
Chỗ tôi được phép sử dụng luôn ko cần chứng minh
HT
????
cho 1 vé báo cáo free nhé
là sao vậy?
Nêu và chứng minh BĐT - Mincopki
Chứng minh bđt sau:
5(x-1)<x5-1<5x4(x-1)nếu x-1>0
Cần chứng minh:
\(5\left(x-1\right)< x^5-1< 5x^4\left(x-1\right)\)
\(5\left(x-1\right)< \left(x-1\right)\left(x^4+x^3+x^2+x+1\right)< 5x^4\left(x-1\right)\)
\(5< x^4+x^3+x^2+x+1< 5x^4\)
Vì \(x>1\)
\(\Rightarrow x^4>x^3>x^2>x>1\)
Vậy ta có ĐPCM
chứng minh các bđt sau
\(x^2+y^2+z^2+3\ge2\left(x+y+z\right)\)
\(x^2+y^2+z^2+3\ge2\left(x+y+z\right)\)
<=>\(x^2+y^2+z^2+3-2x-2y-2z\ge0\)
<=>\(\left(x^2-2x+1\right)+\left(y^2-2y+1\right)+\left(z^2-2z+1\right)\ge0\)
<=>\(\left(x-1\right)^2+\left(y-1\right)^2+\left(z-1\right)^2\ge0\)
chứng minh các bđt sau:
\(\frac{cosx+sinx}{cos^2x}=tan^3x+tan^2x+tanx+1\)
Bạn xem lại đề, đề của bạn không phải BĐT
Chứng minh nếu a+b<0 thì ít nhất 1 trong 2 BĐT sau sai a^3+3a^2b>=0,b^3+3ab^2>=0
\(x\sqrt{x}+y\sqrt{y}+z\sqrt{z}\ge\frac{1}{\sqrt{3}}\)
Chứng minh BĐT trên bằng BĐT Cosi
mn cho e hỏi cách chứng minh bđt cộng mẫu ạ
Chứng minh \(\dfrac{a^2}{x}+\dfrac{b^2}{y}+\dfrac{c^2}{z}\ge\dfrac{\left(a+b+c\right)^2}{x+y+z}với\left(x;y;z>0\right)\)
Thường thì sẽ sử dụng cái này nhiều nhất
Đầu tiên đi chứng minh
\(\dfrac{a^2}{x}+\dfrac{b^2}{y}\ge\dfrac{\left(a+b\right)^2}{x+y}\\ \Leftrightarrow\dfrac{a^2y+b^2x}{xy}\ge\dfrac{a^2+2ab+b^2}{x+y}\\ \Leftrightarrow a^2xy+\left(bx\right)^2+\left(ay\right)^2+b^2xy\ge a^2xy+2abxy+b^2xy\\ \Leftrightarrow\left(ay\right)^2+\left(bx\right)^2-2abxy\ge0\Leftrightarrow\left(ay-bx\right)^2\ge0\left(đúng\right)\)
Áp dụng 1 lần nữa ta có điều ở trên
Dấu $=$ xảy ra $⇔\dfrac{a}{x}=\dfrac{b}{y}=\dfrac{c}{z}$