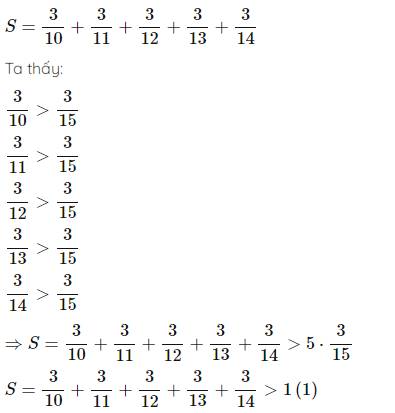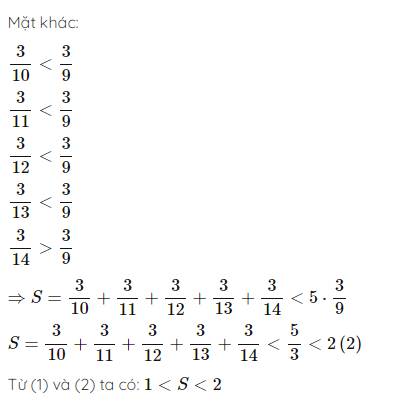chứng minh \(3^{2^{10}}-1⋮2^{12}\)
DH
Những câu hỏi liên quan
1.Chứng minh rằng: √2 + √6 +√12 + √20 < 12
2. Cho A=1/5+2/(5^2)+3/(5^3)+......+10/(5^10)+11/(5^11). Chứng minh rằng A < 5/16
1.a,chứng minh 12^4.54^2=36^5
b,10^6-5^7 chia hết cho 59
c,cho S=1+3^1+3^2+3^3…+3^99 chứng minh S chia hết cho 4, S chia hết cho 40
2. Tính: 10^4.27^3/6^4.15^4
a)Cho A= 3/10+3/11+3/12+3/13+3/14.
Chứng minh A<3/2
b)Cho B=1/11+1/12+1/13+....+1/20.
Chứng minh 7/12<B<5/6c
c)Cho C=1/5+1/6+....+1/17
Chứng minh C>1
Cho A= 3/10 + 3/11 + 3/12 + 3/13 + 3/14. Chứng minh rằng: 1 < A < 2
Cho S = 3/10 + 3/11+3/12+3/13+3/14 . Chứng minh rằng 1 nhỏ hơn S nhỏ hơn 2
\(S=\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}\)
\(\Rightarrow S< \dfrac{3}{10}+\dfrac{3}{10}+\dfrac{3}{10}+\dfrac{3}{10}+\dfrac{3}{10}\)
\(\Rightarrow S< \dfrac{15}{10}< 2\)
Lại có \(S>\dfrac{3}{14}+\dfrac{3}{14}+\dfrac{3}{14}+\dfrac{3}{14}+\dfrac{3}{14}\)
\(\Rightarrow S>\dfrac{15}{14}>1\)
\(\Rightarrow1< S< 2\)
Đúng 3
Bình luận (0)
Cho S = 3/10 + 3/11+3/12+3/13+3/14 . Chứng minh rằng 1 nhỏ hơn S nhỏ hơn 2
Tính :M=1/1*2*3+1/2*3*4+1/3*4*5+...+1/10*11*12Chứng minh rằng :A=1/1^2+1/2^2+1/3^2+...+1/50^2<2
Xem chi tiết
chứng minh rằng A= 12/1*4*7+12/4*7*10+12/7*10*13+...+12/54*57*60<1/2
giải giup minh nha minh tich cho
////????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????không biết
Đúng 0
Bình luận (0)
Cho S= \(\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}\)
Chứng minh rằng: 1<S<2
Ta có: \(\dfrac{3}{10}>\dfrac{3}{15}\)
\(\dfrac{3}{11}>\dfrac{3}{15}\)
\(\dfrac{3}{12}>\dfrac{3}{15}\)
\(\dfrac{3}{13}>\dfrac{3}{15}\)
\(\dfrac{3}{14}>\dfrac{3}{15}\)
Do đó: \(\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}>\dfrac{3}{15}+\dfrac{3}{15}+\dfrac{3}{15}+\dfrac{3}{15}+\dfrac{3}{15}=1\)
hay 1<S(1)
Ta có: \(\dfrac{3}{11}< \dfrac{3}{10}\)
\(\dfrac{3}{12}< \dfrac{3}{10}\)
\(\dfrac{3}{13}< \dfrac{3}{10}\)
\(\dfrac{3}{14}< \dfrac{3}{10}\)
Do đó: \(\dfrac{3}{11}+\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}< \dfrac{3}{10}+\dfrac{3}{10}+\dfrac{3}{10}+\dfrac{3}{10}=\dfrac{12}{10}\)
\(\Leftrightarrow S< \dfrac{15}{10}=\dfrac{3}{2}< 2\)(2)
Từ (1) và (2) suy ra 1<S<2(đpcm)
Đúng 4
Bình luận (1)
Thịnh đúng rồi
Bạn làm hay quá
Xem thêm câu trả lời
Cho S=3/10+3/11+3/12+3/13+3/14 Chứng minh:1<S<2
\(S=\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}\)
Ta thấy:
\(\dfrac{3}{10}>\dfrac{3}{15}\\\dfrac{3}{11}>\dfrac{3}{15}\\ \dfrac{3}{12}>\dfrac{3}{15}\\ \dfrac{3}{13}>\dfrac{3}{15}\\ \dfrac{3}{14}>\dfrac{3}{15} \)
\(\Rightarrow S=\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}>5\cdot\dfrac{3}{15}\\ S=\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}>1\left(1\right)\)
Mặt khác:
\(\dfrac{3}{10}< \dfrac{3}{9}\\ \dfrac{3}{11}< \dfrac{3}{9}\\ \dfrac{3}{12}< \dfrac{3}{9}\\ \dfrac{3}{13}< \dfrac{3}{9}\\ \dfrac{3}{14}>\dfrac{3}{9}\)
\(\Rightarrow S=\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}< 5\cdot\dfrac{3}{9}\\ S=\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}< \dfrac{5}{3}< 2\left(2\right)\)
Từ (1) và (2) ta có: \(1< S< 2\)
Đúng 0
Bình luận (0)