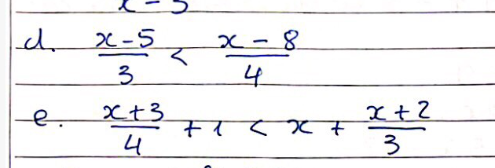 giải BPT sau
giải BPT sau
BN
Những câu hỏi liên quan
Giải các bpt sau:
Đọc tiếp
Giải các bpt sau:
Giải các bpt sau:
Đọc tiếp
Giải các bpt sau:
e, ĐK: \(x\ne2\)
\(\dfrac{3}{x-2}>1\Leftrightarrow\dfrac{5-x}{x-2}>0\)
\(\Leftrightarrow\left\{{}\begin{matrix}5-x>0\\x-2>0\end{matrix}\right.\left(1\right)\) hoặc \(\left\{{}\begin{matrix}5-x< 0\\x-2< 0\end{matrix}\right.\left(2\right)\)
\(\left(1\right)\Leftrightarrow2< x< 5\)
\(\left(2\right)\Leftrightarrow\) vô nghiệm
Vậy \(2< x< 5\)
f, ĐK: \(x\ne\dfrac{1}{2}\)
\(\dfrac{2x^2+x}{1-2x}\ge1-x\)
\(\Leftrightarrow\dfrac{2x^2+x+\left(x-1\right)\left(1-2x\right)}{\left(1-2x\right)\left(x-1\right)}\ge0\)
\(\Leftrightarrow\dfrac{4x-1}{\left(1-2x\right)\left(x-1\right)}\ge0\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x-1\ge0\\\left(1-2x\right)\left(x-1\right)>0\end{matrix}\right.\left(1\right)\) hoặc \(\left\{{}\begin{matrix}4x-1\le0\\\left(1-2x\right)\left(x-1\right)< 0\end{matrix}\right.\left(2\right)\)
\(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{1}{4}\\\dfrac{1}{2}< x< 1\end{matrix}\right.\Leftrightarrow\dfrac{1}{2}< x< 1\)
\(\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{1}{4}\\\left[{}\begin{matrix}x>1\\x< \dfrac{1}{2}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow x\le\dfrac{1}{4}\)
Vậy ...
Đúng 1
Bình luận (0)
Giải các pt, bpt sau:
\(\dfrac{x+1}{x+2}-\dfrac{5}{x-2}=\dfrac{20}{4-x^2}\) (\(ĐK:x\)≠\(2;-2\))
⇔ \(\dfrac{\left(x+1\right)\left(x-2\right)-5\left(x+2\right)}{x^2-4}=\dfrac{20}{4-x^2}\)
⇔ \(-\left(x+1\right)\left(x-2\right)+5\left(x+2\right)=20\)
⇔ \(-\left(x^2-2x+x-2\right)+5x+10=20\)
⇔ \(-x^2+x+2+5x+10-20=0\)
⇔ \(-x^2+6x-8=0\)
⇔ \(-\left(x^2-6x+9\right)=-1\)
⇔ \(\left(x-3\right)^2=1\)
⇔ \(\left[{}\begin{matrix}x-3=1\\x-3=-1\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}x=4\\x=2\end{matrix}\right.\)
Vậy ...
Đúng 1
Bình luận (0)
b: \(\Leftrightarrow20-5\left(3x+2\right)>4\left(x+7\right)\)
=>20-15x-10>4x+28
=>-15x+10-4x-28>0
=>-19x-18>0
=>-19x>18
hay x<-18/19
Đúng 0
Bình luận (0)
Giải bpt sau:
-1/(x-2)≥0
Ta có: \(-\dfrac{1}{x-2}\ge0\)
nên x-2<0
hay x<2
Đúng 2
Bình luận (0)
\(-\dfrac{1}{x-2}\ge0\Leftrightarrow x-2\le0\Leftrightarrow x\le2\)
Mà : $x ≠ 2 $
Do đó, bất phương trình vô nghiệm
Đúng 0
Bình luận (0)
\(\dfrac{-1}{x-2}\ge0\)
ĐKXĐ: \(x-2\ne0\Leftrightarrow x\ne2\)
\(\Leftrightarrow-1\left(x-2\right)\ge0\)
\(\Leftrightarrow x-2\le0\)
\(\Leftrightarrow x\le2\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(không-thõa-mãn-ĐKXĐ\right)\\x< 2\left(thỏa-mãn-ĐKXĐ\right)\end{matrix}\right.\)
Vậy \(S=\left\{x|x< 2\right\}\)
Đúng 0
Bình luận (0)
Giải BPT sau
-x+5 > 9-2x
\(\Leftrightarrow-x+2x>9-5\)
\(\Leftrightarrow x>4\)
Đúng 6
Bình luận (1)
`-x+5 > 9-2x`
`<=>-x+2x > 9-5`
`<=>x > 4`
Vậy `S={x|x > 4}`
Đúng 4
Bình luận (1)
-x+5 > 9-2x
\(\Leftrightarrow-x+5-9+2x>0\)
\(\Leftrightarrow x-4>0\Leftrightarrow x>4\)
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
Giải bpt sau: x(x-1) > 0
\(x\left(x-1\right)>0\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>0\\x-1>0\end{matrix}\right.\\\left\{{}\begin{matrix}x< 0\\x-1< 0\end{matrix}\right.\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x>1\\x< 0\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Giải bpt sau:
\(\dfrac{x-1}{4-x}\text{≥}0\)
\(bpt\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-1\ge0\\4-x>0\end{matrix}\right.\\\left\{{}\begin{matrix}x-1\le0\\4-x< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge1\\x< 4\end{matrix}\right.\\\left\{{}\begin{matrix}x\le1\\x>4\end{matrix}\right.\end{matrix}\right.\Leftrightarrow1\le x< 4\)
Vậy .......
Đúng 4
Bình luận (0)
\(\left[{}\begin{matrix}\left\{{}\begin{matrix}x-1\ge0\\4-x>0\end{matrix}\right.\\\left\{{}\begin{matrix}x-1\le0\\4-x< 0\end{matrix}\right.\end{matrix}\right.\)⇔\(\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge1\\x< 4\end{matrix}\right.\\\left\{{}\begin{matrix}x\le1\\x>4\end{matrix}\right.\end{matrix}\right.\)
Vậy....
Đúng 0
Bình luận (1)
giải bpt sau: 3x-5>-2x+5
3x-5>-2x+5
⇔ 3x+2x > 5+5
⇔ 5x >5
⇔ x>1
vậy bpt có tập nghiệm là S={ x/ x>1}
Đúng 0
Bình luận (0)
Giải bpt sau:
|5 - 2x| - 2|x - 1| ≤ 5x + 3
giải bpt sau
1-3x<0
1-3x<0
<=> -3x<-1
<=> x> -1/-3
<=> x> 1/3
1-3x<0
<=> -3x<-1
<=> x<\(\frac{-1}{-3}\)
<=> x<\(\frac{1}{3}\)








