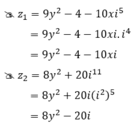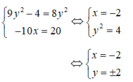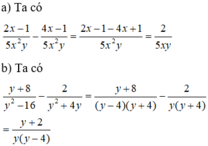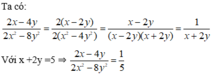B(y) = 8y2 + 5
TN
Những câu hỏi liên quan
Tìm số thực x,y để hai số phức z1 9y2 - 4 - 10xi5 và z2 8y2 + 20i11 là liên hợp của nhau?
z
1
9
y
2
-
4
-
10
x
i
5
v
à
z
2
8
y
2...
Đọc tiếp
Tìm số thực x,y để hai số phức z1 = 9y2 - 4 - 10xi5 và z2 = 8y2 + 20i11 là liên hợp của nhau? z 1 = 9 y 2 - 4 - 10 x i 5 v à z 2 = 8 y 2 + 20 i 11 l à
A. x = -2; y = 2.
B. x = 2; y = ±2.
C. x = 2; y = 2.
D. x = -2; y = ±2.
Làm tính trừ các phân thức sau:a)
2
x
−
1
5
x
2
y
−
4
x
−
1
5
x
2
y
với
x
≠
0
và
y
≠
0
;b)...
Đọc tiếp
Làm tính trừ các phân thức sau:
a) 2 x − 1 5 x 2 y − 4 x − 1 5 x 2 y với x ≠ 0 và y ≠ 0 ;
b) y + 8 y 2 − 16 − 2 y 2 + 4 y với y ≠ 0 và y ≠ ± 4
Đưa thừa số ra ngoài dấu căn: 8 y 2 với y > 0
8 y 2 = 4 . 2 y 2 = 2 y 2 = - 2 y 2 ( với y < 0 )
Đúng 0
Bình luận (0)
tìm các số nguyên x,y biết : 4x2 +8y2+8xy+4y-8=0
=>4x^2+8xy+4y^2+4y^2+4y+1-9=0
=>(2x+2y)^2+(2y+1)^2=9
mà x,y nguyên
nên (2y+1)^2=9 và (2x+2y)^2=0
=>x+y=0 và \(2y+1\in\left\{3;-3\right\}\)
=>\(\left(x,y\right)\in\left\{\left(-1;1\right);\left(2;-2\right)\right\}\)
Đúng 0
Bình luận (0)
chứng tỏ
a) x2 + 8y2 =( x +2y ) ( x2- 2xy +4y2)
b) (x-y) (x2+xy+y2 ) -3xy (x-y) =( x-y)3
c) (x-3y) (x2 +3xy +9y2 ) - ( 3y +x ) ( 9y2 -3xy + x2) = -54y3
cíu em vớii
\(a,VP=\left(x+2y\right)\left(x^2-2xy+4y^2\right)\\ =\left(x+2y\right)\left[x^2-x.2y+\left(2y\right)^2\right]\\ =x^3+\left(2y\right)^3=x^3+8y^3=VT\left(đpcm\right)\\ b,VT=\left(x-y\right)\left(x^2+xy+y^2\right)-3xy\left(x-y\right)\\ =x^3-y^3-3xy\left(x-y\right)\\ =x^3-3x^2y+3xy^2-y^3\\ =\left(x-y\right)^3=VP\left(đpcm\right)\)
Đúng 0
Bình luận (0)
\(c,VT=\left(x-3y\right)\left(x^2+3xy+9y^2\right)-\left(3y+x\right)\left(9y^2-3xy+x^2\right)\\ =\left(x-3y\right)\left[x^2+x.3y+\left(3y\right)^2\right]-\left(x+3y\right).\left[x^2-x.3y+\left(3y\right)^2\right]\\ =x^3-27y^3-\left(x^3+27y^3\right)\\ =-54y^3=VP\left(đpcm\right)\)
Đúng 0
Bình luận (0)
Tính
(x/x+y-x+2y/2y).(x/x-2y-1+8y2/8y3-x3
Tính giá trị của biểu thức 2 x - 4 y 2 x 2 - 8 y 2 với x + 2y = 5
(x-2y).(x2+2xy+4y2)-(x-y).(x2+8y2)
mọi người giúp em giải bài này với ạ
\(\left(x-2y\right)\left(x^2+2xy+4y^2\right)-\left(x-y\right)\left(x^2+8y^2\right)\)
\(=x^3-8y^3-\left(x^3-x^2y+8xy^2-8y^3\right)\)
\(=x^3-8y^3-x^3+x^2y-8xy^2+8y^3\)
\(=x^2y-8xy^2\)
Đúng 1
Bình luận (0)
\(\left(x-2y\right)\left(x^2+2xy+4y^2\right)-\left(x-y\right)\left(x^2+8y^2\right)\\ =x^3-8y^3-\left(x^3+8y^3-x^2y-8y^3\right)\\ =x^3-8y^3-x^3-8y^3+x^2y+8y^3\\ =-8y^3+x^2y\)
Đúng 0
Bình luận (0)
Cho x+y =1 tính giá trị của m=8x2 + 16x2y + 16xy2 + 8y2- 5x - 5y + 2018
\(8x^2+16x^2y+16xy^2+8y^2-5x-5y+2018\)
\(=8\left(x^2+y^2\right)+16xy\left(x+y\right)-5\left(x+y\right)+2018\)
\(=8\left[\left(x+y\right)^2-2xy\right]+16xy\left(x+y\right)-5\left(x+y\right)+2018\)
\(=8\left(x+y\right)^2-16xy+16xy\left(x+y\right)-5\left(x+y\right)+2018\)
\(=8\left(x+y\right)^2-16xy\left[1-\left(x+y\right)\right]-5\left(x+y\right)+2018\)
\(=8.1^2-16xy\left(1-1\right)-5.1+2018\)
\(=8-0-5+2018\)
\(=2021\)
!!!Chúc học tốt!!!
Đúng 0
Bình luận (0)
Tìm số thực x; y để hai số phức z1 9y2 – 4 – 10xi5 và z2 8y2 + 20i11 là liên hợp của nhau? A. x -2; y 2. B. x 2; y ±2. C. x 2; y 2. D. x -2; y ±2.
Đọc tiếp
Tìm số thực x; y để hai số phức z1 = 9y2 – 4 – 10xi5 và z2 = 8y2 + 20i11 là liên hợp của nhau?
A. x = -2; y = 2.
B. x = 2; y = ±2.
C. x = 2; y = 2.
D. x = -2; y = ±2.
Chọn D.
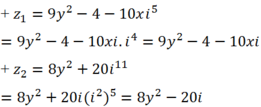
+ z1 và z2 là liên hợp của nhau khi và chỉ khi:
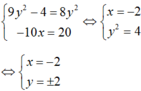
Đúng 0
Bình luận (0)