a: =>x(x+3)=0

=>x=0 hoặc x=-3

b: =>x(1-2x)=0

=>x=0 hoặc x=1/2

c: =>(x-7)(2x+3-x)=0

=>(x-7)(x+3)=0

=>x=7 hoặc x=-3

d: =>(x-2)(3x-1-x-3)=0

=>(x-2)(2x-4)=0

=>x=2

a)

`x^2 +3x=0`

`<=>x(x+3)=0`

\(< =>\left[{}\begin{matrix}x=0\\x+3=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=0\\x=-3\end{matrix}\right.\)

b)

`x-2x^2 =0`

`<=>x(1-2x)=0`

\(< =>\left[{}\begin{matrix}x=0\\1-2x=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\end{matrix}\right.\)

c)

`(x-7)(2x+3)=x(x-7)`

`<=>(x-7)(2x+3)-x(x-7)=0`

`<=>(x-7)(2x+3-x)=0`

`<=>(x-7)(x+3)=0`

\(< =>\left[{}\begin{matrix}x-7=0\\x+3=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=7\\x=-3\end{matrix}\right.\)

d)

`(x-2)(x+3)=(x-2)(3x-1)`

`<=>(x-2)(x+3)-(x-2)(3x-1)=0`

`<=>(x-2)(x+3-3x+1)=0`

`<=>(x-2)(-2x+4)=0`

\(< =>\left[{}\begin{matrix}x-2=0\\-2x+4=0\end{matrix}\right.\\ < =>x=2\)

a)\(x^2+3x=0\)

<=>x(x+3)=0

x=0 hoặc x+3=0

x=0 hoặc x=-3

b)x-2x²=0

x(1-2x)=0

x=0 hoặc 1-2x=0

x=0 hoặc x=0,5

c)(x-7)(2x+3)=4(x-7)

(x-7)(2x+3)-4(x-7)=0

(x-7)(2x+3-4)=0

x-7=0 hoặc 2x+3-4=0

x=7 hoặc x=0,5

d)(x-2)(x+3)=(x-2)(3x-1)

(x-2)(x+3)-(x-2)(3x-1)=0

(x-2)(x+3-3x+1)=0

x-2=0 hoặc x+3-3x+1=0

x=2 hoặc x-3x=-3-1

               -2x=-4

               x=2

\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)

\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)

\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)

\(\Leftrightarrow x^2-9-x^2+3x=0\)

\(\Leftrightarrow3x-9=0\)

\(\Leftrightarrow3x=9\)

\(\Leftrightarrow x=3\left(n\right)\)

Vậy \(S=\left\{3\right\}\)

\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)

\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)

\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)

\(\Leftrightarrow12x-9-12x+20+2x-7>0\)

\(\Leftrightarrow2x+4>0\)

\(\Leftrightarrow2x>-4\)

\(\Leftrightarrow x>-2\)

\(a,2x\left(x-5\right)+4\left(x-5\right)=0\\ \Leftrightarrow\left(x-5\right)\left(2x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-5=0\\2x+4=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=5\\2x=-4\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=5\\x=-2\end{matrix}\right.\)

Vậy \(x\in\left\{5;-2\right\}\)

\(b,3x-15=2x\left(x-5\right)\\ \Leftrightarrow3\left(x-5\right)-2x\left(x-5\right)=0\\ \Leftrightarrow\left(x-5\right)\left(-2x+3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-5=0\\-2x+3=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=5\\2x=3\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{3}{2}\end{matrix}\right.\)

Vậy \(x\in\left\{5;\dfrac{3}{2}\right\}\)

\(c,\left(2x+1\right)\left(3x-2\right)=\left(5x-8\right)\left(2x+1\right)\\ \Leftrightarrow\left(2x+1\right)\left(3x-2\right)-\left(5x-8\right)\left(2x+1\right)=0\\ \Leftrightarrow\left(2x+1\right)\left(3x-2-5x+8\right)=0\\ \Leftrightarrow\left(2x+1\right)\left(-2x+6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x+1=0\\-2x+6=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}2x=-1\\2x=6\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=3\end{matrix}\right.\)

Vậy \(x\in\left\{-\dfrac{1}{2};3\right\}\)

Câu d xem lại đề

a) |3x| = x + 6 (1)

Ta có 3x = 3x khi x ≥ 0 và 3x = -3x khi x < 0

Vậy để giải phương trình (1) ta quy về giải hai phương trình sau:

+ ) Phương trình 3x = x + 6 với điều kiện x ≥ 0

Ta có: 3x = x + 6 ⇔ 2x = 6 ⇔ x = 3 (TMĐK)

Do đó x = 3 là nghiệm của phương trình (1).

+ ) Phương trình -3x = x + 6 với điều kiện x < 0

Ta có -3x = x + 6 ⇔ -4x + 6 ⇔ x = -3/2 (TMĐK)

Do đó x = -3/2 là nghiệm của phương trình (1).

Vậy tập nghiệm của phương trình đã cho S = {3; -3/2}

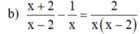
ĐKXĐ: x ≠ 0, x ≠ 2

Quy đồng mẫu hai vễ của phương trình, ta được:

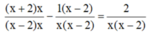
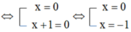
Vậy tập nghiệm của phương trình là S = {-1}

c) (x + 1)(2x – 2) – 3 > –5x – (2x + 1)(3 – x)

⇔ 2x2 – 2x + 2x – 2 – 3 > –5x – (6x – 2x2 + 3 – x)

⇔ 2x2 – 5 ≥ –5x – 6x + 2x2 – 3 + x

⇔ 10x ≥ 2 ⇔ x ≥ 1/5

Tập nghiệm: S = {x | x ≥ 1/5}

Đoán xem

đoán thử nào

(x + 2)(x - 2) + 3x^2 = (2x + 1)^2 + 2x 

<=> x^2 - 4 + 3x^2 = 4x^2 + 4x + 1 + 2x

<=> x^2 - 4 + 3x^2 = 4x^2 + 6x + 1

<=> x^2 - 4 + 3x^2 - 4x^2 - 6x - 1 = 0

<=> -5 - 6x = 0

<=> -6x = 5

<=> x = -5/6

a) ĐKXĐ: \(x\notin\left\{-1;0\right\}\)

Ta có: \(\dfrac{x+3}{x+1}+\dfrac{x-2}{x}=2\)

\(\Leftrightarrow\dfrac{x\left(x+3\right)}{x\left(x+1\right)}+\dfrac{\left(x+1\right)\left(x-2\right)}{x\left(x+1\right)}=\dfrac{2x\left(x+1\right)}{x\left(x+1\right)}\)

Suy ra: \(x^2+3x+x^2-3x+2=2x^2+2x\)

\(\Leftrightarrow2x^2+2-2x^2-2x=0\)

\(\Leftrightarrow-2x+2=0\)

\(\Leftrightarrow-2x=-2\)

hay x=1(nhận)

Vậy: S={1}

b) ĐKXĐ: \(x\notin\left\{-7;\dfrac{3}{2}\right\}\)

Ta có: \(\dfrac{3x-2}{x+7}=\dfrac{6x+1}{2x-3}\)

\(\Leftrightarrow\left(3x-2\right)\left(2x-3\right)=\left(6x+1\right)\left(x+7\right)\)

\(\Leftrightarrow6x^2-9x-4x+6=6x^2+42x+x+7\)

\(\Leftrightarrow6x^2-13x+6-6x^2-43x-7=0\)

\(\Leftrightarrow-56x-1=0\)

\(\Leftrightarrow-56x=1\)

hay \(x=-\dfrac{1}{56}\)(nhận)

Vậy: \(S=\left\{-\dfrac{1}{56}\right\}\)

c) ĐKXĐ: \(x\ne-\dfrac{2}{3}\)

Ta có: \(\dfrac{5}{3x+2}=2x-1\)

\(\Leftrightarrow5=\left(3x+2\right)\left(2x-1\right)\)

\(\Leftrightarrow6x^2-3x+4x-2-5=0\)

\(\Leftrightarrow6x^2+x-7=0\)

\(\Leftrightarrow6x^2-6x+7x-7=0\)

\(\Leftrightarrow6x\left(x-1\right)+7\left(x-1\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(6x+7\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\6x+7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\6x=-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(nhận\right)\\x=-\dfrac{7}{6}\left(nhận\right)\end{matrix}\right.\)

Vậy: \(S=\left\{1;-\dfrac{7}{6}\right\}\)

d) ĐKXĐ: \(x\ne\dfrac{2}{7}\)

Ta có: \(\left(2x+3\right)\cdot\left(\dfrac{3x+8}{2-7x}+1\right)=\left(x-5\right)\left(\dfrac{3x+8}{2-7x}+1\right)\)

\(\Leftrightarrow\left(2x+3\right)\cdot\left(\dfrac{3x+8+2-7x}{2-7x}\right)-\left(x-5\right)\left(\dfrac{3x+8+2-7x}{2-7x}\right)=0\)

\(\Leftrightarrow\left(2x+3-x+5\right)\cdot\dfrac{-4x+6}{2-7x}=0\)

\(\Leftrightarrow\left(x+8\right)\cdot\left(-4x+6\right)=0\)(Vì \(2-7x\ne0\forall x\) thỏa mãn ĐKXĐ)

\(\Leftrightarrow\left[{}\begin{matrix}x+8=0\\-4x+6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-8\\-4x=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-8\left(nhận\right)\\x=\dfrac{3}{2}\left(nhận\right)\end{matrix}\right.\)

Vậy: \(S=\left\{-8;\dfrac{3}{2}\right\}\)

=>\(\dfrac{3x^3-9x^2+9x-2x^3+2x^2-6x}{\left(x^2-3x+3\right)\left(x^2-x+3\right)}=-1\)

=>x^3-7x^2+3x=-[(x^2+3)^2-4x(x^2+3)+3x^2]

=>x^3-7x^2+3x+(x^2+3)^2-4x(x^2+3)+3x^2=0

=>x^3-4x^2+3x+x^4+6x^2+9-4x^3-12x=0

=>x^4-3x^3+2x^2-9x+9=0

=>(x-3)(x-1)(x^2+x+3)=0

=>x=3;x=1

\(\dfrac{3x}{x^2-x+3}-\dfrac{2x}{x^2-3x+3}+1=0\left(a\right)\)

Ta có : \(x^2-x+3=x^2-x+\dfrac{1}{4}+\dfrac{11}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{11}{4}>0\)

\(x^2-3x+3=x^2-3x+\dfrac{9}{4}+\dfrac{3}{4}=\left(x-\dfrac{3}{2}\right)^2+\dfrac{3}{4}>0\)

\(\RightarrowĐKXĐ:x\in R\)

Đặt : \(t=x^2-x+3\)

\(\left(a\right)\Leftrightarrow\dfrac{3x}{t}-\dfrac{2x}{t-2x}+1=0\)

\(\Leftrightarrow3x\left(t-2x\right)-2xt+t\left(t-2x\right)=0\)

\(\Leftrightarrow t^2-xt-6x^2=0\)

\(\Leftrightarrow t^2+2xt-3xt-6x^2=0\)

\(\Leftrightarrow t\left(t+2x\right)-3x\left(t+2x\right)=0\)

\(\Leftrightarrow\left(t-3x\right)\left(t+2x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}t-3x=0\\t+2x=0\end{matrix}\right.\left(b\right)\)

Thay ​\(t=x^2-x+3\) ​lại vào (b) được :

\(\left[{}\begin{matrix}x^2-x+3-3x=0\\x^2-x+3+2x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x^2-4x+3=0\\x^2+x+3=0\end{matrix}\right.\left(c\right)\)

Mà : \(x^2-4x+3=x^2-x-3x+3\)

\(=x\left(x-1\right)-3\left(x-1\right)=\left(x-1\right)\left(x-3\right)\left(c'\right)\)

và : \(x^2+x+3=x^2+x+\dfrac{1}{4}+\dfrac{11}{4}\)

\(=\left(x+\dfrac{1}{2}\right)^2+\dfrac{11}{4}\left(c''\right)\)

Thay (c') và (c'') vào (c) được :

\(\left[{}\begin{matrix}\left(x-1\right)\left(x-3\right)=0\\\left(x+\dfrac{1}{2}\right)^2+\dfrac{11}{4}=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x-1=0\Leftrightarrow x=1\left(tmđk\right)\\x-3=0\Leftrightarrow x=3\left(tmđk\right)\end{matrix}\right.\\\left(x+\dfrac{1}{2}\right)^2=-\dfrac{11}{4}\Leftrightarrow x\in\varnothing\end{matrix}\right.\)

Vậy : Phương trình có tập nghiệm \(S=\left\{1;3\right\}\)