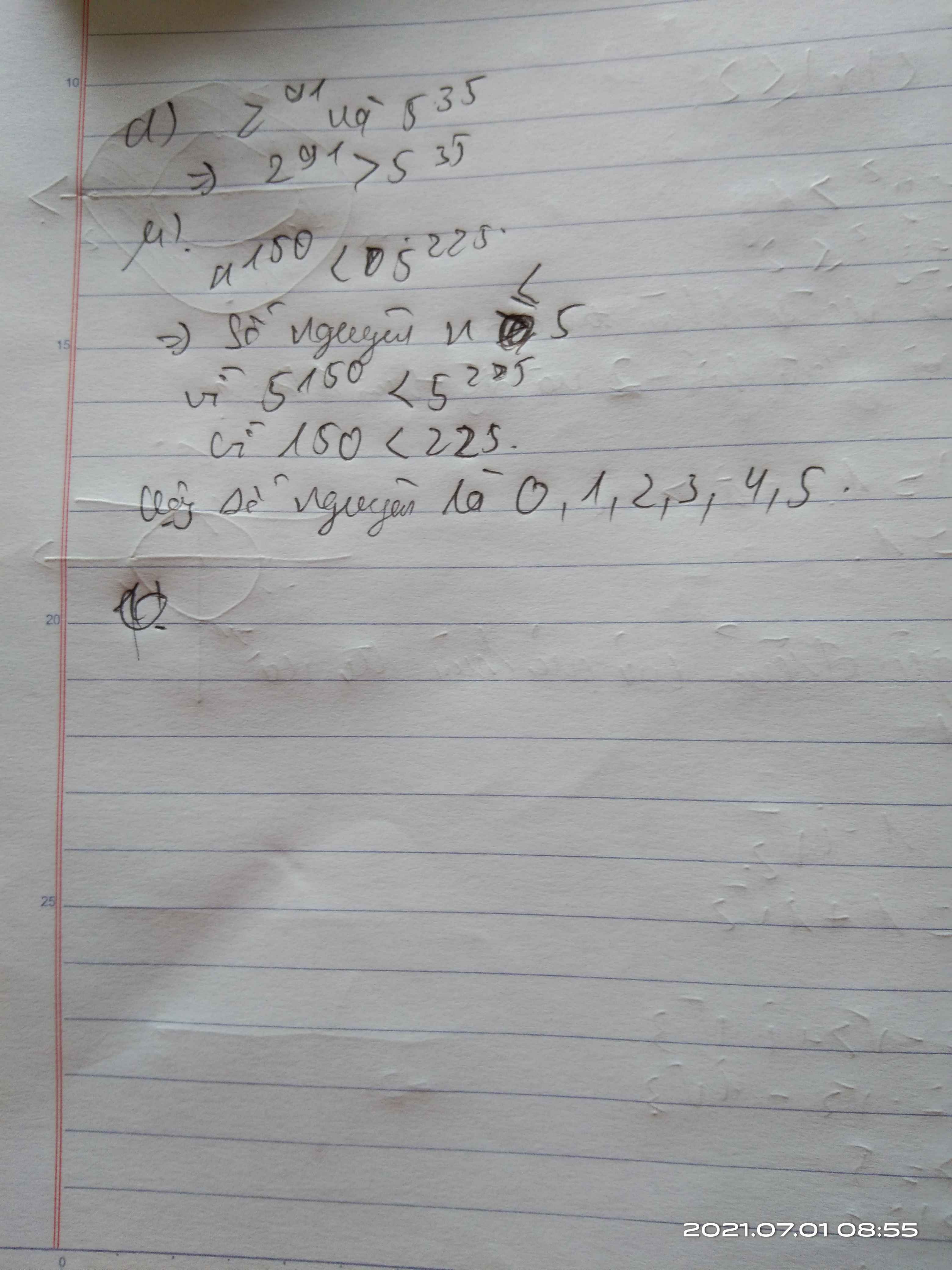Tìm số nguyên n lớn nhất sao cho \(n^{150}< 5^{225}\)
NN
Những câu hỏi liên quan
Tìm số nguyên n lớn nhất sao cho :n^150<5^225
n^150<5^225
(n^2)^75<(5^3)^75
n^2<5^3
n^2<125
mà n lớn nhất nên n^2=121
n=11
chính xác 100%
Đúng 0
Bình luận (0)
ai giải đúng và nhanh mình sẽ k
Đúng 0
Bình luận (0)
Tìm số nguyên N lớn nhất sao cho n^150 < 5^225
n150<5225
=>(n2)75<(53)75
=>n2<53=125
=>n<12
=>max n=11
vậy max n=11 max là giá trị lớn nhất
Đúng 1
Bình luận (0)
Ta có n^150 < 5^225
=>n^150 = n^2 x 75
=>5^225 = 5^3 x 75
Mà n^2 < 5^3 ( 5^3 = 125 )
Còn n^2 < 125
Ta thử 12^2 = 144
11^2 = 121
Vì 144 > 125 >121
Nên kết quả bằng 11^2
Vậy kết quả: n=11
Đúng 0
Bình luận (0)
Tìm số nguyên n lớn nhất sao cho n^150<5^225
Ta có: n^150 < 5^225
<=> n^2^75< 5^3^75
<=> n^2 < 5^3= 125
<=> n^2 ≤ 121
<=>n ≤11
mà n lớn nhất nên n=11
Vậy n=11
Đúng 0
Bình luận (0)
tìm số nguyên tố n lớn nhất sao cho n^150<5^225
Ta có: n^150 < 5^225
<=> n^2^75< 5^3^75
<=> n^2 < 5^3= 125
<=> n^2 ≤ 121
<=>n ≤11
mà n lớn nhất nên n=11
Vậy n=11
Đúng 0
Bình luận (0)
a) so sánh \(2^{91}\) & \(5^{35}\)
b) Tìm số nguyên n lớn nhất sao cho \(n^{150}<5^{225}\)
b) Ta có: \(n^{150}< 5^{225}\)
\(\Leftrightarrow\left(n^2\right)^{75}< \left(5^3\right)^{75}\)
\(\Leftrightarrow n^2< 125\)
\(\Leftrightarrow n=11\)
Đúng 0
Bình luận (0)
Tìm số nguyên n lớn nhất sao cho n150 < 5225
Tìm số nguyên n lớn nhất sao cho \(n^{150}< 5^{225}\)
\(n^{150}=\left(n^2\right)^{75};5^{225}=\left(5^3\right)^{75}=125^{75}\)
\(n^{150}< 5^{225}\) hay \(\left(n^2\right)^{75}< 125^{75}\)
=> \(n^2< 125\)
Nên: Số nguyên lớn nhất thỏa mãn điều kiện trên là n=11
Đúng 0
Bình luận (0)
Ta có: n^150 < 5^225
<=> n^2^75< 5^3^75
<=> n^2 < 5^3= 125
<=> n^2 ≤ 121
<=>n ≤11
mà n lớn nhất nên n=11
Vậy n=11
Đúng 0
Bình luận (0)
tìm số nguyên lớn nhất sao cho n150<5225
(n2)75 > (53)75
vay n2 > 125
can bac 2 cua 121=11
vay n = 11
t i c k nah
Đúng 0
Bình luận (0)
tìm số nguyên lớn nhất sao cho n150<5225
\(n^{150}< 5^{225}\)
\(\Rightarrow\left(n^2\right)^{75}< \left(5^3\right)^{75}\)
\(\Rightarrow n^2< 5^3=125\)
\(\Rightarrow n< 12\)
\(\Rightarrow\) Gía trị nguyên lớn nhất của n là 11
Đúng 0
Bình luận (0)