giải thích vì sao:
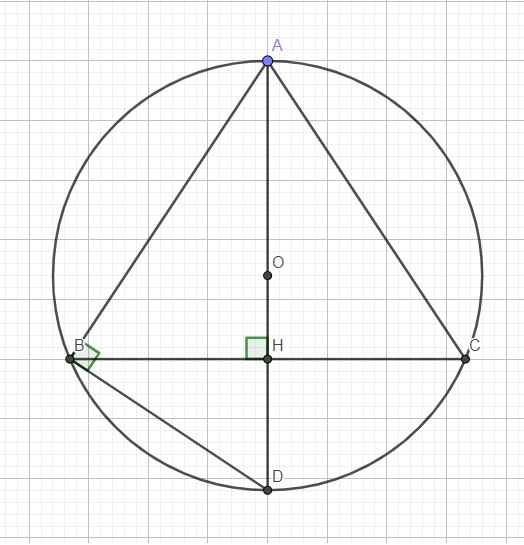
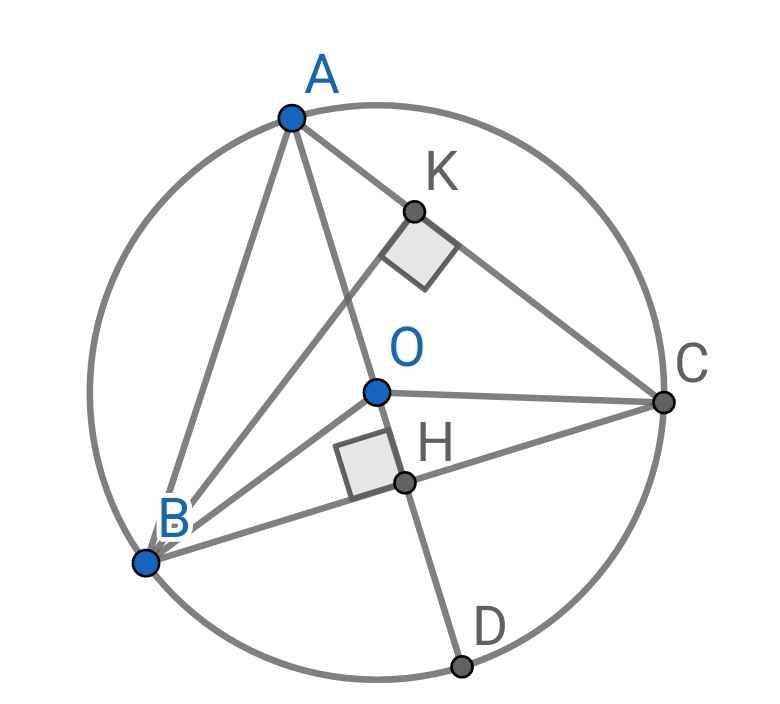
1. cho tam giác ABC đường cao AH. (O;r), (O1;r1),(O2;r2) theo thứ tự là các ddwwongf tròn nội tếp tam giác ABC,ABH,ACH
Vì sao r/BC=r1/AB=r2/AC
2.(O;r) nội tiếp tam giác ABC. CÁc tieeps tuyến với (O) // với các cạnh tam giác cắt tgiac thành 3 tgiac nho. r1,r2,r3 là bkinh các đường tròn của các tgiac nhỏ đó.
vì sao r1+r2+r3 / r = P1+P2+P3 / P