\(\left\{{}\begin{matrix}x-2y=3\\2x+3y=-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=3+2y\\2\left(3+2y\right)+3y=-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=3+2y\\6+4y+3y=-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=3+2y\\7y=-7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=3+2\left(-1\right)\\y=-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x-4y=6\\2x+3y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=3+2y=3-2=1\end{matrix}\right.\)

\(4\left(8x^3-12x^2+6x-1\right)+3\left(2x-1\right)-3\sqrt{1-y}-4\left(1-y\right)\sqrt{1-y}=0\)

\(\Leftrightarrow4\left(2x-1\right)^3+3\left(2x-1\right)-3\sqrt{1-y}-4\left(1-y\right)\sqrt{1-y}=0\)

Đặt \(\left\{{}\begin{matrix}2x-1=a\\\sqrt{1-y}=b\end{matrix}\right.\)

\(4\left(a^3-b^3\right)+3\left(a-b\right)=0\)

\(\Leftrightarrow\left(a-b\right)\left[4\left(a^2+ab+b^2\right)+3\right]=0\)

\(\Rightarrow a=b\Rightarrow2x-1=\sqrt{1-y}\Rightarrow x\ge\frac{1}{2}\)

\(y=1-\left(2x-1\right)^2\) thay xuống pt dưới

 ĐKXĐ: \(x,y\ne0\)\(\left\{{}\begin{matrix}x+y+\dfrac{1}{x}+\dfrac{1}{y}=4\\x^3+y^3+\dfrac{1}{x^3}+\dfrac{1}{y^3}=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+\dfrac{1}{x}+y+\dfrac{1}{y}=4\\\left(x+\dfrac{1}{x}\right)^3+\left(y+\dfrac{1}{y}\right)^3-3\left(x+\dfrac{1}{x}\right)-3\left(y+\dfrac{1}{y}\right)=4\end{matrix}\right.\)

Đặt \(x+\dfrac{1}{x}=a;y+\dfrac{1}{y}=b\left(a,b\ne0\right)\)

\(\Rightarrow hpt\) trở thành:

\(\left\{{}\begin{matrix}a+b=4\left(1\right)\\a^3+b^3-3a-3b=4\left(2\right)\end{matrix}\right.\) 

Từ (1) \(\Rightarrow a=4-b\) Thay vào (2) ta được:

\(\left(4-b\right)^3+b^3-3\left(4-b\right)-3b=4\Leftrightarrow64-48b+12b^2-b^3+b^3-12+3b-3b-4=0\Leftrightarrow12b^2-48b+60=0\Leftrightarrow b^2-4b+5=0\Leftrightarrow b^2-4b+4+1=0\Leftrightarrow\left(b-2\right)^2+1=0\) Vô lí \(\Rightarrow\) ko có a,b \(\Rightarrow\) ko có x,y

Vậy hpt vô nghiệm

Bây giờ a giải đc hệ này chưa ạ? Nếu giải đc r cho e xin lời giải đc ko ạ

\(\left\{{}\begin{matrix}x+y=80\\2x+3y=198\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}3x+3y=240\\2x+3y=198\end{matrix}\right.\)

\(\left\{{}\begin{matrix}x+y=80\\x=240-198=42\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=42\\y=38\end{matrix}\right.\)

\(\left\{{}\begin{matrix}x+y=80\\2x+3y=198\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}2x+2y=160\\2x+3y=198\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}y=38\\2x+3\cdot38=198\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}y=38\\2x=84\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}y=38\\x=42\end{matrix}\right.\)

Vậy (42;38) là nghiệm

\(\left\{{}\begin{matrix}x+y=500\\\dfrac{8}{10}x+\dfrac{9}{10}y=420\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=500-y\\\dfrac{8}{10}\left(500-y\right)+\dfrac{9}{10}y=420\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=500-y\\400+\dfrac{y}{10}=420\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=500-y=300\\y=200\end{matrix}\right.\)

Vậy (x,y)=(300,200)

hpt <=> \(\left\{{}\begin{matrix}\dfrac{8}{10}x+\dfrac{8}{10}y=400\\\dfrac{8}{10}x+\dfrac{9}{10}y=420\end{matrix}\right.\)

<=>\(\left\{{}\begin{matrix}x+y=500\\\dfrac{1}{10}y=20\end{matrix}\right.\)

<=> \(\left\{{}\begin{matrix}x+y=500\\y=200\end{matrix}\right.\)

<=>\(\left\{{}\begin{matrix}x=300\\y=200\end{matrix}\right.\)

(Các phần giải thích học sinh không phải trình bày).

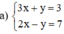 (Vì hệ số của y ở 2 pt đối nhau nên cộng từng vế của 2 pt).

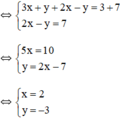
Vậy hệ phương trình có nghiệm duy nhất (2; -3).

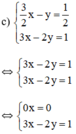
Phương trình 0x = 0 nghiệm đúng với mọi x nên hệ phương trình có vô số nghiệm dạng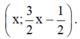 

KL: Đồ thị hai hàm số trên trùng nhau. Vậy hệ phương trình có vô số nghiệm