Δ=(-2)^2-4(-2m+1)

=4+8m-4=8m

Để phương trình có nghiệm thì 8m>=0

=>m>=0

\(x_2^2\left(x_1^2-1\right)+x_1^2\left(x_2^2-1\right)=8\)

=>\(2\cdot\left(x_1\cdot x_2\right)^2-x_2^2-x_1^2=8\)

=>\(2\cdot\left(-2m+1\right)^2-\left[\left(x_1+x_2\right)^2-2x_1x_2\right]=8\)

=>\(2\left(2m-1\right)^2-\left[2^2-2\left(-2m+1\right)\right]=8\)

=>\(8m^2-8m+2-4+2\left(-2m+1\right)=8\)

=>\(8m^2-8m-2-4m+2-8=0\)

=>8m^2-12m-8=0

=>m=2 hoặc m=-1/2(loại)

a: Khi m=-1 thì phương trình sẽ là:

x^2-(-3-1)x+2-1-1=0

=>x^2+4x=0

=>x=0 hoặc x=-4

Yêu cầu đề là gì vậy bạn?

\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)

\(=\left(\dfrac{7}{2}\right)^2-2.3\)

\(=\dfrac{25}{4}\)

x1^2+x2^2=(x1+x2)^2-2x1x2

=49/4-2*3=49/4-6

=25/4

\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\left(\dfrac{7}{2}\right)^2-3.2=\dfrac{49}{4}-6=\dfrac{25}{4}\)

Áp dụng định lí vi- et ta có:   x 1 + x 2 = 3 x 1 . x 2 = 1

Ta có: x 1 2 + x 2 2 = x 1 + x 2 2 - 2 x 1 . x 2 = 3 2 - 2 . 1 = 7 .

b) Theo định lí Vi-et ta có:

c) Theo định lí Vi-et ta có:

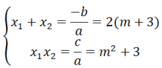
P = x 1 2 + x 2 2  = (x1 + x2 )2 - 2 x 1 x 2  = 4 m + 3 2  - 2( m 2  + 3)

= 4( m 2  + 6m + 9) - 2( m 2  + 3) = 2 m 2  + 24m + 30