
giúp mik giải bài này vs![]()
![]() mik đag cần gấp
mik đag cần gấp

giúp mik giải bài này vs![]() mik đag cần gấp
mik đag cần gấp
a.
Do MA là tiếp tuyến tại A \(\Rightarrow MA\perp OA\Rightarrow\widehat{MAO}=90^0\)
Xét hai tam giác OMA và OMB có:
\(\left\{{}\begin{matrix}OA=OB=R\\MA=MB\left(gt\right)\\OM\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OMA=\Delta OMB\left(c.c.c\right)\)
\(\Rightarrow\widehat{MBO}=\widehat{MAO}=90^0\)
\(\Rightarrow MB\perp OB\Rightarrow MB\) là tiếp tuyến
b.
Gọi H là giao điểm AB và OM
Ta có: \(\left\{{}\begin{matrix}OA=OB=R\\MA=MB\left(gt\right)\end{matrix}\right.\) \(\Rightarrow OM\) là trung trực AB
\(\Rightarrow OM\perp AB\) tại H đồng thời \(HA=HB=\dfrac{AB}{2}\)
Trong tam giác vuông OMA: \(cos\widehat{AOM}=\dfrac{OA}{OM}=\dfrac{2}{2R}=\dfrac{1}{2}\Rightarrow\widehat{AOM}=60^0\)
\(\Rightarrow\widehat{AMO}=90^0-\widehat{AOM}=30^0\)
\(\Rightarrow\widehat{AMB}=2\widehat{AMO}=60^0\)
\(\Rightarrow\Delta AMB\) đều (tam giác cân có 1 góc bằng 60 độ)
Trong tam giác vuông OAH:
\(AH=OA.sin\widehat{AOM}=R.sin60^0=\dfrac{R\sqrt{3}}{3}\)
\(\Rightarrow AB=2AH=R\sqrt{3}\)
\(OH=OA.cos\widehat{AOM}=R.cos30^0=\dfrac{R}{2}\)
\(\Rightarrow HM=OM-OH=\dfrac{3R}{2}\)
\(\Rightarrow S_{ABM}=\dfrac{1}{2}HM.AB=\dfrac{3R^2\sqrt{3}}{4}\)
c.
BE là đường kính \(\Rightarrow\widehat{BAE}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{BAE}=90^0\Rightarrow AB\perp AE\)
Mà \(AB\perp OM\) (theo cm câu b)
\(\Rightarrow AE||OM\) (cùng vuông góc AB)
Giúp mik giải bài 1 vs mik đag cần gấp cảm ơn trc ạ

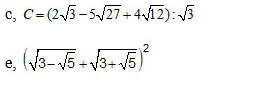
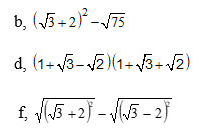 các bạn giải hộ mik mấy câu này vs mik đag cần gấp
các bạn giải hộ mik mấy câu này vs mik đag cần gấp
c, \(C=\left(2\sqrt{3}-5\sqrt{27}+4\sqrt{12}\right):\sqrt{3}\)
<=> \(C=\left(2\sqrt{3}-15\sqrt{3}+8\sqrt{3}\right):\sqrt{3}\)
<=> \(C=-5\sqrt{3}:\sqrt{3}=-5\)
e. \(\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)^2\)
\(=3-\sqrt{5}+3+\sqrt{5}+2\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\)
\(=6+2\sqrt{9-5}\)
\(=6+4=10\)
b. \(\left(\sqrt{3}+2\right)^2-\sqrt{75}\)
\(=3+4\sqrt{3}+4-5\sqrt{3}\)
\(=7-\sqrt{3}\)
d. \(\left(1+\sqrt{3}-\sqrt{2}\right)\left(1+\sqrt{3}+\sqrt{2}\right)\)
\(=\left(1+\sqrt{3}\right)^2-2\)
\(=1+2\sqrt{3}+3-2\)
\(=2+2\sqrt{3}\)
f. \(\sqrt{\left(\sqrt{3}+2\right)^2}-\sqrt{\left(\sqrt{3}-2\right)^2}\)
\(=\left|\sqrt{3}+2\right|-\left|\sqrt{3}-2\right|\)
\(=\sqrt{3}+2-2+\sqrt{3}\)
\(=2\sqrt{3}\)
c: Ta có: \(C=\left(2\sqrt{3}-5\sqrt{27}+4\sqrt{12}\right):\sqrt{3}\)
\(=\left(2\sqrt{3}-5\cdot3\sqrt{3}+4\cdot2\sqrt{3}\right):\sqrt{3}\)
\(=2-15+8=-5\)
d: Ta có: \(D=\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)^2\)
\(=3-\sqrt{5}+3+\sqrt{5}+2\cdot\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\)
\(=6+2\cdot2=10\)
 Giúp mik bài 4 vs mn, mik đag cần gấp
Giúp mik bài 4 vs mn, mik đag cần gấp
Xét tam giác PMO và QNO có PMO=QNO=90 độ (gt) và POM=QON (2 góc đối đỉnh)
=>tam giác PMO đồng dạng QNO =>PM=QN=x=2,5 =)
Giúp mik bài 4 vs ạ mik đag cần gấp
giải hộ bài văn nghị luận này vs thankyou
đề bài hãy tìm các ý để triển khai luận điểm trẻ em cần phải nghe lời cha mẹ
giải hộ mik vs mik đag cần gấp
Thank you
Trong mặt phẳng Oxy , cho đường thẳng (d): y=m2x+3m+2 và đường thẳng (d1): y= x+ 5 . Tìm giá trị của m để hai đường thẳng song song với nhau.
giúp mik giải bài này vs ![]()
![]() mik đag cần gấp
mik đag cần gấp
Hai đường thẳng đã cho song song khi và chỉ khi:
\(\left\{{}\begin{matrix}m^2=1\\3m+2\ne5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=\pm1\\m\ne1\end{matrix}\right.\)
\(\Rightarrow m=-1\)
Bạn nào giúp mik 3 bài này với
Mik cảm ơn ạ
Vì mik đag gấp á nên mong các bạn giúp mik vs

Bài 3:
b: Xét ΔABC có
I là trung điểm của BC
IK//AC
Do đó: K là trung điểm của AB
Xét ΔABC có
I là trung điểm của BC
IH//AB
Do đó: H là trung điểm của AC
Xét ΔABC có
K là trung điểm của AB
H là trung điểm của AC
Do đó: HK là đường trung bình của ΔABC
Suy ra: HK//BC
Mn ơi giúp mik giải bài này vs mik cần gấp ạ >