NB
Những câu hỏi liên quan
M.Bài 6.Cho hai đường tròn (O; R) và (O; R) tiếp xúc ngoài nhau tại M. Hai đường tròn (O) và (O) cùng tiếp xúc trong với đường tròn lớn (O; R) lần lượt tại E và F. Tính bán kính Rbiết chu vi tam giác OOOlà 20cm.Bài 7.Cho đường tròn (O; 9cm). Vẽ 6 đường tròn bằng nhau bán kính R đều tiếp xúc trong với (O) và mỗi đường tròn đều tiếp xúc với hai đường khác bên cạnh nó. Tính bán kính R.Bài 8.Cho hai đường tròn đồng tâm. Trong đường tròn lớn vẽ hai dây bằng nhau AB CD và cùng tiếp xúc với...
Đọc tiếp
M.Bài 6.Cho hai đường tròn (O; R) và (O; R) tiếp xúc ngoài nhau tại M. Hai đường tròn (O) và (O) cùng tiếp xúc trong với đường tròn lớn (O; R) lần lượt tại E và F. Tính bán kính Rbiết chu vi tam giác OOOlà 20cm.
Bài 7.Cho đường tròn (O; 9cm). Vẽ 6 đường tròn bằng nhau bán kính R đều tiếp xúc trong với (O) và mỗi đường tròn đều tiếp xúc với hai đường khác bên cạnh nó. Tính bán kính R.
Bài 8.Cho hai đường tròn đồng tâm. Trong đường tròn lớn vẽ hai dây bằng nhau AB = CD và cùng tiếp xúc với đường tròn nhỏ tại M và N sao cho AB CD tại I. Tính bán kính đường tròn nhỏ biết IA = 3cm, IB = 9cm.
Bài 9.Cho ba đường tròn O O O1 2 3( ),( ),( )cùng có bán kính R và tiếp xúc ngoài nhau từng đôi một. Tính diện tích tam giác có ba đỉnh là ba tiếp điểm.
Bài 10.Cho hai đường tròn (O) và (O) tiếp xúc nhau tại A. Qua A vẽ một cát tuyến cắt đường tròn (O) tại B và cắt đường tròn (O) tại C. Từ B vẽ tiếp tuyến xyvới đường tròn (O). Từ C vẽ đường thẳng uv song song với xy. Chứng minh rằng uvlà tiếp tuyến của đường tròn (O).
Bài 11.Cho hình vuông ABCD. Vẽ đường tròn (D; DC) và đường tròn (O) đường kính BC, chúng cắt nhau tại một điểm thứ hai là E. Tia CE cắt AB tại M, tia BE cắt AD tại N. Chứng minh rằng:a) N là trung điểm của AD.b) M là trung điểm của AB.
Bài 12.Cho góc vuông xOy. Lấy các điểm I và K lần lượt trên các tia Oxvà Oy. Vẽ đường tròn (I; OK) cắt tia Oxtại M (I nằm giữa O và M). Vẽ đường tròn (K; OI) cắt tia Oytại N (K nằm giữa O và N).
a) Chứng minh hai đường tròn (I) và (K) luôn cắt nhau.
b) Tiếp tuyến tại M của đường tròn (I) và tiếp tuyến tại N của đường tròn (K) cắt nhau tại C. Chứng minh tứ giác OMCN là hình vuông.
c) Gọi giao điểm của hai đường tròn (I), (K) là A và B. Chứng minh ba điểm A, B, C thẳng hàng.d) Giả sử I và K theo thứ tự di động trên các tia Oxvà Oysao cho OI + OK = a(không đổi). Chứng minh rằng đường thẳng AB luôn đi qua một điểm cố định.
Cho hai đường tròn (O;R) và (O'R') (R>R')tiếp xúc trong tại A. Một tiếp tuyến của đường tròn (O') tại M cắt đường tròn (O) tại hai điểm B,C. Đường thẳng BO' cắt đường tròn (O) tại điểm thứ hai là D và cắt đường thẳng AM tại E. Gọi F là giao điểm thứ hai của đường tròn ngoại tiếp tam giác ADE với AC. Chứng minh rằng DF là phân giác của góc BDC.
Gọi B', C' lần lượt là giao điểm khác A của AB, AC với (O').
Do BM, CM là tiếp tuyến của (O') nên ta dễ dàng chứng minh được:
\(BM^2=BA.BB'\); \(CM^2=CA.CC'\)
\(\Rightarrow\dfrac{BM^2}{CM^2}=\dfrac{BA.BB'}{CA.CC'}\). (1)
\(\Delta AOC\sim\Delta AO'C'(g.g)\Rightarrow \frac{AC}{AC'}=\frac{AO}{AO'}\).
Tương tự, \(\frac{AB}{AB'}=\frac{AO}{AO'}\).
Do đó \(\dfrac{AB}{AB'}=\dfrac{AC}{AC'}\Rightarrow\dfrac{AB}{BB'}=\dfrac{AC}{CC'}\Rightarrow\dfrac{AB}{AC}=\dfrac{BB'}{CC'}\). (2)
Từ (1), (2) suy ra \(\dfrac{BM}{CM}=\dfrac{AB}{AC}\).
Theo tính chất đường phân giác đảo thì AM là đường phân giác ngoài của tam giác ABC
\(\Rightarrow\widehat{MAB}+\widehat{MAC}=180^o\Rightarrow180^o+\widehat{BAC}=2\widehat{EAC}\)
\(\Rightarrow180^o-\widehat{EAC}=\dfrac{180^o-\widehat{BAC}}{2}\). (3)
Các tứ giác FDEA, DBAC nội tiếp nên \(\widehat{FDB}=180^o-\widehat{EAC};\widehat{BDC}=180^o-\widehat{BAC}\). (4)
Từ (3), (4) suy ra \(\widehat{FDB}=\dfrac{\widehat{BDC}}{2}\) nên DF là phân giác góc BDC.
Đúng 1
Bình luận (0)
Cho đường tròn (O) và một điểm M cố định không nằm trên đường tròn. Qua M kẻ hai đường thẳng . Đường thẳng thứ nhất cắt (O) tại A và B. Đường thẳng thứ hai cắt (O) tại C và D. Chứng minh MA.MB = MC.MD.
Hướng dẫn: Xét cả hai trường hợp điểm M nằm bên trong và bên ngoài đường tròn. Trong mỗi trường hợp, xét hai tam giác đồng dạng.
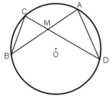
TH1: M nằm trong đường tròn.
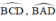là hai góc nội tiếp cùng chắn cung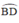 
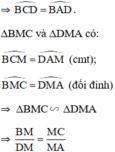
⇒ MA.MB = MC.MD
TH2: M nằm ngoài đường tròn.
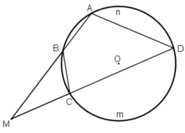
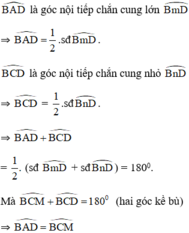
ΔMBC và ΔMDA có:
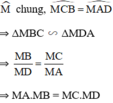
Kiến thức áp dụng
+ Góc nội tiếp chắn một cung có số đo bằng một nửa số đo của cung đó.
+ Hai góc nội tiếp chắn cùng một cung thì có số đo bằng nhau.
Đúng 0
Bình luận (0)
Cho đường tròn (O) và một điểm M cố định không nằm trên đường tròn. Qua M kẻ hai đường thẳng . Đường thẳng thứ nhất cắt (O) tại A và B. Đường thẳng thứ hai cắt (O) tại C và D. Chứng minh MA.MB = MC.MD.
Hướng dẫn: Xét cả hai trường hợp điểm M nằm bên trong và bên ngoài đường tròn. Trong mỗi trường hợp, xét hai tam giác đồng dạng.
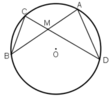
TH1: M nằm trong đường tròn.
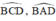là hai góc nội tiếp cùng chắn cung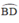 
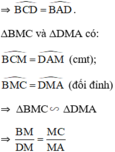
⇒ MA.MB = MC.MD
TH2: M nằm ngoài đường tròn.
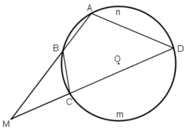
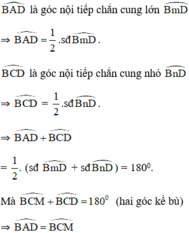
ΔMBC và ΔMDA có:
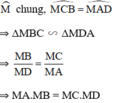
Đúng 1
Bình luận (0)
Cho ba đường thẳng cắt nhau tại ba giao điểm A, B, C.a. Hãy vẽ điểm O sao cho A và O nằm trong một nửa mặt phẳng có bờ là BC, B và O nằm trong một nửa mặt phẳng có bờ là đường thẳng CA và C và O nằm trong một nửa mặt phẳng có bờ là đường thẳng AB.b. Hãy vẽ điểm A’ sao cho A’ và O nằm trong hai nửa mặt phẳng đối nhau có bờ là đường thẳng AB đồng thời A’ và O nằm trong hai nửa mặt phẳng đối nhau có bờ là đường thẳng AC. A’ và O cùng nằm trong một nửa mặt phẳng có bờ là đường thẳng nào?
Đọc tiếp
Cho ba đường thẳng cắt nhau tại ba giao điểm A, B, C.
a. Hãy vẽ điểm O sao cho A và O nằm trong một nửa mặt phẳng có bờ là BC, B và O nằm trong một nửa mặt phẳng có bờ là đường thẳng CA và C và O nằm trong một nửa mặt phẳng có bờ là đường thẳng AB.
b. Hãy vẽ điểm A’ sao cho A’ và O nằm trong hai nửa mặt phẳng đối nhau có bờ là đường thẳng AB đồng thời A’ và O nằm trong hai nửa mặt phẳng đối nhau có bờ là đường thẳng AC. A’ và O cùng nằm trong một nửa mặt phẳng có bờ là đường thẳng nào?
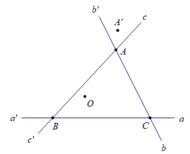
a. Giả sử ba đường thẳng aa’, bb’ và cc’ cắt nhau từng đôi một tại ba điểm A, B, C (hình vẽ). Điểm O cần vẽ là giao điểm của hai tia AO và BO sao cho tia AO nằm giữa hai tia AB và AC, tia BO nằm giữa hai tia BA và BC.
b. Điểm A’ nằm trên tia AA’ sao cho tia AA’ nằm giữa hai tia Ab’ và Ac, A’ và O cùng nằm trong một nửa mặt phẳng có bờ là đường thẳng BC.
Đúng 0
Bình luận (0)
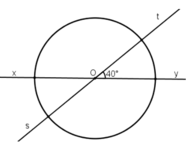
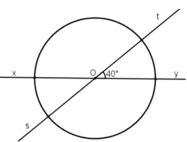
Cho hai đường thẳng xy và st cắt nhau tại O, trong các góc tạo thành có góc 40o. Vẽ một đường tròn tâm O. Tính số đo của các góc ở tâm xác định bởi hai trong bốn tia gốc O.
Cho hai đường thẳng xy và st cắt nhau tại O, trong các góc tạo thành có góc 40 ° . Vẽ một đường tròn tâm O. Tính số đo của các góc ở tâm xác định bởi hai trong bốn tia gốc O.
Cho hai đường thẳng xy và st cắt nhau tại O, trong các góc tạo thành có góc 40o. Vẽ một đường tròn tâm O. Tính số đo của các góc ở tâm xác định bởi hai trong bốn tia gốc O.
Ta có :
\(\widehat{xOs}\)= 400(theo giải thiết)
\(\widehat{tOy}\)=400( đối đỉnh với \(\widehat{xOs}\))
\(\widehat{xOt}\) + \(\widehat{tOy}\)= 1800
\(\Rightarrow\widehat{xOt}\) = \(\widehat{tOy}\) \(=180^0-40^0=140^0\)
\(\widehat{yOs}=140^0\)(đối đỉnh với \(\widehat{xOt}\))
\(\widehat{xOy}=\widehat{sOt}=180^0\)
Đúng 0
Bình luận (0)
Cho 1 điểm M nằm bên ngoài đường tròn (O; 6cm). Kẻ hai tiếp tuyến MN, MP (N, P là hai tiếp điểm) của đường tròn (O). Vẽ cát tuyến MAB của đường trong (O) sao cho đoạn thẳng AB6cm với A, B thuộc đường tròn (O), A nằm giữa M và B.a) Chứng minh tứ giác OPMN là tứ giác nội tiếpb) Gọi H là trung điểm đoạn thẳng AB. So sánh góc MON và góc MHNc) Tính diện tích hình viên phân giới hạn bởi cung nhỏ AB và dây AB của hình tròn tâm (O)
Đọc tiếp
Cho 1 điểm M nằm bên ngoài đường tròn (O; 6cm). Kẻ hai tiếp tuyến MN, MP (N, P là hai tiếp điểm) của đường tròn (O). Vẽ cát tuyến MAB của đường trong (O) sao cho đoạn thẳng AB=6cm với A, B thuộc đường tròn (O), A nằm giữa M và B.
a) Chứng minh tứ giác OPMN là tứ giác nội tiếp
b) Gọi H là trung điểm đoạn thẳng AB. So sánh góc MON và góc MHN
c) Tính diện tích hình viên phân giới hạn bởi cung nhỏ AB và dây AB của hình tròn tâm (O)
a: góc ONM+góc OPM=180 độ
=>ONMP nội tiếp
b: góc OHM=góc ONM=90 độ
=>OHNM nội tiếp
=>góc MON=góc MHN
Đúng 0
Bình luận (0)
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B, trong đó O’ nằm trên đường tròn (O). Kẻ đường kính O’OC của đường tròn (O). Chứng minh rằng CA, CB là các tiếp tuyến của đường tròn (o’)
Tam giác AO’C nội tiếp trong đường tròn (O) có O’C là đường kính nên 
Suy ra: CA ⊥ O’A tại điểm A
Vậy CA là tiếp tuyến của đường tròn (O’)
Tam giác BO’C nội tiếp trong đường tròn (O) có O’C là đường kính nên 
Suy ra: CB ⊥ O’B tại điểm B
Vậy CB là tiếp tuyến của đường tròn (O’)
Đúng 0
Bình luận (0)