Cho tam giác ABC có G là trọng tâm. Phân tích BA theo BC và GC
Giải chi tiết cho mình với ạ
TN
Những câu hỏi liên quan
Cho tam giác ABC có trung tuyến BM và trọng tâm G . Phân tích vecto BG theo hai vecto BA và vecto BC
\(\overrightarrow{BG}=\dfrac{2}{3}\overrightarrow{BM}=\dfrac{2}{3}\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{BC}\)
Đúng 1
Bình luận (0)
giải hộ mình với. Mn viết rõ đủ vì mình làm nộp hôm dự giờ ạ
Cho tam giác ABC
a) Nếu G là trọng tâm tam giác ABC thì vecto GA+ GB+GC = vecto 0
b) Nếu vecto IA+IB+IC=vecto 0 thì I là trọng tâm tam giác ABC
Cho tam giác ABC có G là trọng tâm. D là trung điểm BC. Biết GA=\(2\sqrt{3}\), GB = \(2\sqrt{2}\), GC = 2.
a) Dựng F đối xứng với G qua d. Tính góc GCF?
b) Tính diện tích tam giác ABC.
mình đang cần bài giải gấp cảm ơn ạ!
giúp em với ạ!
Cho tam giác ABC và trọng tâm G của nó. Chứng minh rằng tam giác ABC là tam giác cân khi và chỉ khi AB + GB = AC + GC
Cho tam giác ABC, M là trung điểm BC. M là trung điểm của BC. Lấy điểm D thuộc tia đối của tia BA. Gọi H,K là hình chiếu cú B,C trên DM. Chứng minh G là trọng tâm của tam giác ABC và cũng là trọng tâm của tam giác AHK.
các bạn giúp mình trước 1h với :((( ai làm nhanh đầy đủ mình tick cho ạ
Gọi G là trọng tâm của tam giác ABC\(\frac{\Rightarrow AG}{AM}=\frac{2}{3}\)
Ta có \(\hept{\begin{cases}BM=CM\\\widehat{BHM}=\widehat{CKM}=90^0\\\widehat{BMH}=\widehat{CMK}\end{cases}\Rightarrow\Delta BHM=\Delta CKM\left(\text{ cạnh huyền - góc nhọn}\right)}\)
Vì vậy \(HM=KM\) nên AM là trung tuyến của \(\Delta AHK\) mà \(\frac{AG}{AM}=\frac{2}{3}\Rightarrow G\) là trọng tâm tam giác AHK
Có73thì ứng xử của người khác thì không có lý do của nó là cái gì cũng nên có cái gì cũng nên có cái gì cũng nên nhìn nhận vấn đề theo hướng dẫn của bạn ấy!
Gọi G là trọng tâm tam giác ABC với cạnh huyền BC=12. Tổng hai vecto GB+GC bằng bao nhiêu Mọi người giúp mình giải câu này với
Cho hình bình hành ABCD tâm O. Gọi M, N lần lượt là trung điểm của BC, CD; G là trọng tâm tam giác ABC.
a) Chứng minh AM + AN = 3/2 AC và GA +3GB+GC+GD=0
c) Gọi I là điểm thỏa mãn AI= 3/4AB. Phân tích IN ; IG theo hai vec tơ BA và BC
Chứng minh 3 điểm N;G;I thẳng hàng.
a, Ta có:AM+AN=OM-OA+ON-OA=OM+ON+AC=OC+AC=3/2OC
GA+3GB+GC+OD=2GB+OD=OB+OD=0
C,
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB a; BC 2a và G là trọng tâm. Tính giá trị của biểu thức
G
A
→
.
G
B
→
+
G
B
→
.
G
C
→
+
G
C
→
....
Đọc tiếp
Cho tam giác ABC vuông tại A có AB = a; BC = 2a và G là trọng tâm.
Tính giá trị của biểu thức G A → . G B → + G B → . G C → + G C → . G A
A. -3a2
B. -2a2
C. -4 a2/3
D. 2a2
Chọn C.
Vì ![]() nên
nên
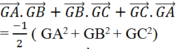
Gọi M, N, P lần lượt là trung điểm của BC, CA, AB
Tam giác ABM đều nên ![]()
Theo định lý Pitago ta có:
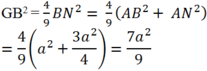
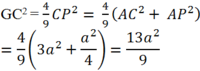
Suy ra
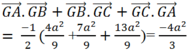
Đúng 0
Bình luận (0)