Cứ solve đi vì cuộc đời cho phép...
\(x^2-x+2=4\sqrt{2x^2-x+1}\)
GPT
A,\(\sqrt{X+1}+\sqrt{4-X}+\sqrt{4+3X-X^2=5}\)
B,\(\sqrt{X^2-2X+5}=2-\left(X^2-1\right)^4\)
C,\(\left(X-5\right)^3=5\sqrt[3]{2X-9}-3X+6\)
D,\(\left(2X+1\right)\sqrt{\frac{X+1}{X}}=X+2+\sqrt[3]{2X^2+X^3}\)
MN ƠI GIÚP E MAI E ĐI HOK RỒI
ETICH CHO AI TRẢ LỜ NHANH NHẤT
Thực hiện phép tính:
a.(2x^2 + 2x - 4) : (x + 2)
b. ( 2x^3 - 5x^2 - x +1 ) : (2x + 1 )
c. (x^3 - 2x + 4)/(x + 2)
d. (x^3- 3x^2): (x - 3)
e. (x^4- x- 14): (x- 2)
f. (x^4- x- 14): (x- 2)
g. (17x^2- 6x^4+ 5x^3- 23x+ 7): (7- 3x^2- 2x)
giúp mik đi ạ mik đang cần gấp T-T
a: \(=\dfrac{2\left(x+2\right)\left(x-1\right)}{x+2}=2x-2\)
b: \(=\dfrac{2x^3+x^2-6x^2-3x+2x+1}{2x+1}=x^2-3x+1\)
c: \(=\dfrac{x^3+2x^2-2x^2-4x+2x+4}{x+2}=x^2-2x+2\)
d: \(=\dfrac{x^2\left(x-3\right)}{x-3}=x^2\)
`@` `\text {Ans}`
`\downarrow`

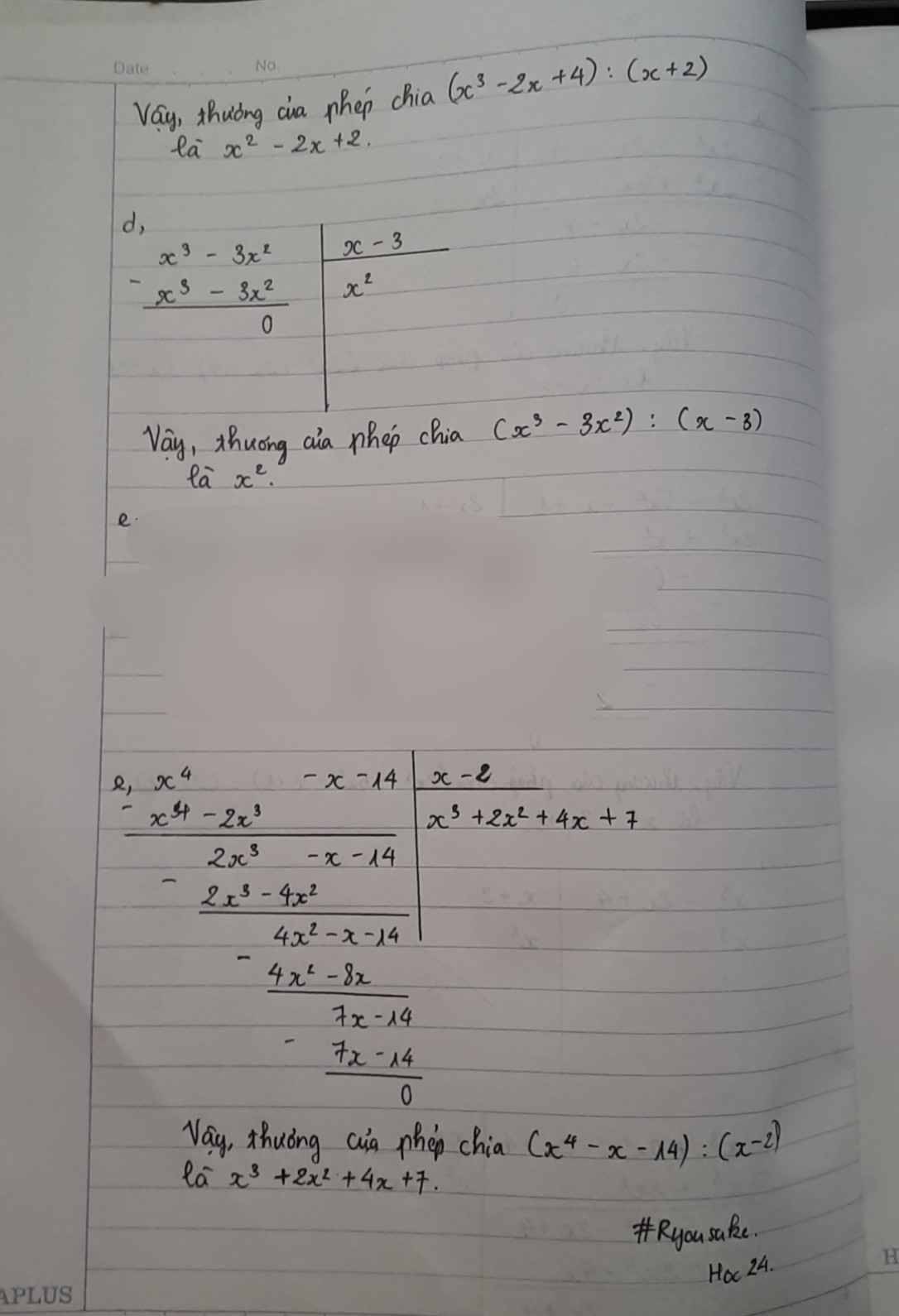

Giải phương trình
a) \(\sqrt{x^2-2x+4}=2x-2\)
b) \(\sqrt{x+2\sqrt{x-1}}=2\)
c) \(\sqrt{2x^2-2x+1}=2x-1\)
d) \(\sqrt{x+4\sqrt{x-4}}=2\)
a.
PT \(\Leftrightarrow \left\{\begin{matrix} 2x-2\geq 0\\ x^2-2x+4=(2x-2)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq 1\\ 3x^2-6x=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq 1\\ 3x(x-2)=0\end{matrix}\right.\Leftrightarrow x=2\)
b. ĐK: $x\geq 1$
PT $\Leftrightarrow \sqrt{(x-1)+2\sqrt{x-1}+1}=2$
$\Leftrightarrow \sqrt{(\sqrt{x-1}+1)^2}=2$
$\Leftrightarrow |\sqrt{x-1}+1|=2$
$\Leftrightarrow \sqrt{x-1}+1=2$
$\Leftrightarrow \sqrt{x-1}=1$
$\Leftrightarrow x=2$ (tm)
c.
PT \(\Leftrightarrow \left\{\begin{matrix} 2x-1\geq 0\\ 2x^2-2x+1=(2x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ 2x^2-2x+1=4x^2-4x+1\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ 2x^2-2x=2x(x-1)=0\end{matrix}\right.\Leftrightarrow x=1\) (tm)
d.
ĐKXĐ: $x\geq 4$
PT $\Leftrightarrow \sqrt{(x-4)+4\sqrt{x-4}+4}=2$
$\Leftrightarrow \sqrt{(\sqrt{x-4}+2)^2}=2$
$\Leftrightarrow |\sqrt{x-4}+2|=2$
$\Leftrightarrow \sqrt{x-4}+2=2$
$\Leftrightarrow \sqrt{x-4}=0$
$\Leftrightarrow x=4$ (tm)
a: Ta có: \(\sqrt{x^2-2x+4}=2x-2\)
\(\Leftrightarrow x^2-2x+4=4x^2-8x+4\)
\(\Leftrightarrow-3x^2+6x=0\)
\(\Leftrightarrow-3x\left(x-2\right)=0\)
\(\Leftrightarrow x=2\)
b: Ta có: \(\sqrt{x+2\sqrt{x-1}}=2\)
\(\Leftrightarrow\left|\sqrt{x-1}+1\right|=2\)
\(\Leftrightarrow\sqrt{x-1}+1=2\)
\(\Leftrightarrow x-1=1\)
hay x=2
c: Ta có: \(\sqrt{2x^2-2x+1}=2x-1\)
\(\Leftrightarrow2x^2-2x+1=4x^2-4x+1\)
\(\Leftrightarrow-2x^2+2x=0\)
\(\Leftrightarrow-2x\left(x-1\right)=0\)
hay x=1
thực hiện phép tính
1/ (\(\sqrt{x}\)+ 1) (\(\sqrt{x}\)- 2)
2/ (x+4) (x-2) - (x-3)^2
3/ 3x (2x^3 - 3x^2 + 5)
Trả lời:
1) \(\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)=\left(\sqrt{x}\right)^2-2\sqrt{x}+\sqrt{x}-2=x-\sqrt{x}-2\)
2) \(\left(x+4\right)\left(x-2\right)-\left(x-3\right)^2=x^2-2x+4x-8-\left(x^2-6x+9\right)\)\(=x^2+2x-8-x^2+6x-9=8x-17\)
3) \(3x\left(2x^3-3x^2+5\right)=6x^4-9x^3+15x\)
Có ý kiến cho rằng: “Cứ sai đi vì cuộc đời cho phép”. Nhưng, cũng có ý kiến khẳng định: “Không nên coi sai lầm là phép thử cho cuộc đời của bạn”. Em hãy trình bày suy nghĩ của mình về các ý kiến trên. Làm thành bài văn giúp mình với ạ. Mình cần gấp lắmm
Suy nghĩ : theo bản thân em, em thấy ý kiến " Cứ sai đi vì cuộc đời cho phép " và " Không nên coi sai lầm là phép thử trong cuộc đời của bạn " là hai câu có ý nghĩ đúng.Chúng ta sẽ cùng làm rõ ý kiến sau :
- " Cứ sai đi vì đời cho phép " : ý kiến này về mặt nghĩa của nó thì cũng có nghĩa đúng,ai sinh ra thì chẳng có lúc phạm phải sai lầm, chính những lần sai trái ấy mới thúc đẩy con người ta trưởng thành hơn. Đời cho phép ta sai vì mong muốn sau những lần sai ấy ta phải lớn khôn, biết sửa sai.
- Và " Không nên coi sai lầm là phép thử cho cuộc đời của bạn ". Ý kiến này cũng đúng, vì khi ta giết người, xâm hại tình dục, ... những việc làm ấy ta chỉ coi là phép thử.. Nhưng thử nghĩ đến hậu quả nghiêm trọng về việc này, khi ta đã giết người mà chỉ " xin lỗi " , " xin lỗi " không thể trở lại ban đầu, không thể làm nạn nhân tỉnh lại .Vì chính điều đó, là những gì ta làm nên những thứ sai lầm, mà ta cứ nghĩ đó là phép thử cuộc đời.
giải các PT sau :
a) \(\left|2x+3\right|-\left|x\right|+\left|x-1\right|=2x+4\)
b) \(\sqrt{x}-\dfrac{4}{\sqrt{x+2}}+\sqrt{x+2}=0\)
c) \(\sqrt{x+\sqrt{2x-1}}+\sqrt{x-\sqrt{2x-1}}=\sqrt{2}\)
d) \(x+\sqrt{x+\dfrac{1}{2}+\sqrt{x+\dfrac{1}{4}}}=4\)
e) \(\sqrt{4x+3}+\sqrt{2x+1}=6x+\sqrt{8x^2+10x+3}-16\)
f)\(\sqrt[3]{x-2}+\sqrt{x+1}=3\)
GIÚP MÌNH VỚI MÌNH ĐANG CẦN GẤP
giai cac phuong trinh
a)\(2x^4+5x^3+x^2+5x+2=0\)
b)\(\sqrt{x-1}-\sqrt[3]{2-x}=1\)
c)\(x-\sqrt{x}+1=\sqrt{2x^2-30x+2}\)
d)\(2x^2+3x+7=\left(x-5\right)\sqrt{2x^2+1}\)
e)\(\sqrt{x-2}+\sqrt{4-x}=2x^2-5x-1\)
BÀI 1:Giải các phương trình
a) \(x^2\)+ 5x - \(\sqrt{x^2+5x+4}\)= -2
b) \(\sqrt{x^2-3x+2}\)+\(\sqrt{x+3}\) = \(\sqrt{x-2}\)+ \(\sqrt{x^2+2x-3}\)
Bài 2: Thực hiện phép tính
\(\frac{\sqrt{2x+2\sqrt{x^2-4}}}{\sqrt{x^2-4}+x+2}\) với x=2\(\sqrt{6}\)+3
a) Điều kiện xác định của pt :
\(\begin{cases}x^2+5x+4\ge0\\x^2+5x+2\ge0\end{cases}\) \(\Leftrightarrow\left[\begin{array}{nghiempt}x\le-4\\x\ge-1\end{array}\right.\)
Ta có : \(x^2+5x-\sqrt{x^2+5x+4}=-2\)
\(\Leftrightarrow\left(x^2+5x+4\right)-\sqrt{x^2+5x+4}-2=0\)(1)
Đặt \(t=\sqrt{x^2+5x+4},t\ge0\)
\(pt\left(1\right)\Leftrightarrow t^2-t-2=0\Leftrightarrow\left(t+1\right)\left(t-2\right)=0\Leftrightarrow\left[\begin{array}{nghiempt}t=-1\left(\text{loại}\right)\\t=2\left(\text{nhận}\right)\end{array}\right.\)
Với t = 2 ta có pt : \(x^2+5x+4=4\Leftrightarrow x\left(x+5\right)=0\Leftrightarrow\left[\begin{array}{nghiempt}x=0\left(\text{nhận}\right)\\x=-5\left(\text{nhận}\right)\end{array}\right.\)
Vậy tập nghiệm của pt : \(S=\left\{-5;0\right\}\)
b) Điều kiện xác định của pt :
\(\begin{cases}x^2-3x+2\ge0\\x+3\ge0\\x-2\ge0\\x^2+2x-3\ge0\end{cases}\) \(\Leftrightarrow x\ge2\)
Ta có ; \(\sqrt{x^2-3x+2}+\sqrt{x+03}=\sqrt{x-2}+\sqrt{x^2+2x-3}\)
\(\Leftrightarrow\sqrt{\left(x-1\right)\left(x-2\right)}+\sqrt{x+3}=\sqrt{x-2}+\sqrt{\left(x-1\right)\left(x+3\right)}\)
\(\Leftrightarrow\sqrt{x-1}\left(\sqrt{x-2}-\sqrt{x-3}\right)-\left(\sqrt{x-2}-\sqrt{x-3}\right)=0\)
\(\Leftrightarrow\left(\sqrt{x-1}-1\right)\left(\sqrt{x-2}-\sqrt{x-3}\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}\sqrt{x-1}-1=0\\\sqrt{x-2}-\sqrt{x-3}=0\end{array}\right.\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=2\left(\text{nhận}\right)\\-2=-3\left(\text{vô lí - loại}\right)\end{array}\right.\)
Vậy pt có nghiệm x = 2
giải pt :
a, \(\sqrt{x-\sqrt{x^2-1}}+\sqrt{x+\sqrt{x^2-1}}=2\)
b, \(\left(x^2+2\right)^2+4\left(x+1\right)^3+\sqrt{x^2+2x+5}=\left(2x-1\right)^2+2\)
c, \(\sqrt{4x^2+x+6}=4x-2+7\sqrt{x+1}\)
d, \(\sqrt{x-2}-\sqrt{x+2}=2\sqrt{x^2-4}-2x+2\)