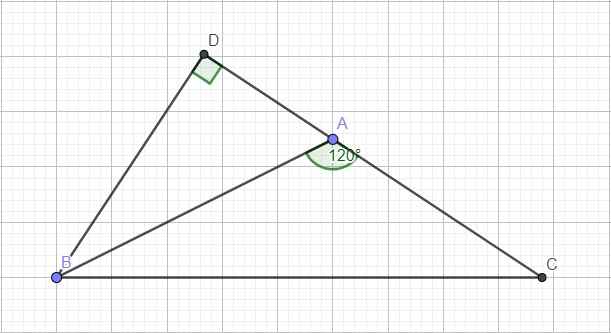
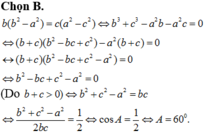Cho tam giác ABC nhọn, BC=a, AC=b, AB=c. Chứng minh rằng: a2=a2+c2-2ab.cosA.
LK
Những câu hỏi liên quan
Cho tam giác ABC có góc A = 120 độ, BC = a, AC = b, AB = c. Chứng minh rằng a2 = b2 + c2 + bc ?
Kẻ đường cao BD ứng với AC. Do góc A tù \(\Rightarrow\) D nằm ngoài đoạn thẳng AC hay \(CD=AD+AC\) và \(\widehat{DAB}=180^0-120^0=60^0\)
Áp dụng định lý Pitago:
\(AB^2=BD^2+AD^2\) \(\Rightarrow BD^2=AB^2-AD^2\)
Trong tam giác vuông ABD:
\(cos\widehat{BAD}=\dfrac{AD}{AB}\Rightarrow\dfrac{AD}{AB}=cos60^0=\dfrac{1}{2}\Rightarrow AD=\dfrac{1}{2}AB\)
\(\Rightarrow BD^2=AB^2-\left(\dfrac{1}{2}AB^2\right)=\dfrac{3}{4}AB^2\)
Pitago tam giác BCD:
\(BC^2=BD^2+CD^2=\dfrac{3}{4}AB^2+\left(AD+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\left(\dfrac{1}{2}AB+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\dfrac{1}{4}AB^2+AB.AC+AC^2\)
\(=AB^2+AB.AC+AC^2\)
Hay \(a^2=b^2+c^2+bc\)
Đúng 3
Bình luận (0)
Trong tam giác ABC. Chứng minh rằng
a) Góc A nhọn khi và chỉ khi a2 < b2 + c2
b) Góc A tù khi và chỉ khi a2 > b2 + c2
c) Góc A vuông khi và chỉ khi a2 = b2 + c2
Trong tam giác ABC, theo Hệ quả định lý Cô sin ta luôn có :
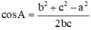
Mà ta có 2.bc > 0 nên cos A luôn cùng dấu với b2 + c2 – a2.
a) Góc A nhọn ⇔ cos A > 0 ⇔ b2 + c2 – a2 > 0 ⇔ a2 < b2 + c2.
b) Góc A tù ⇔ cos A < 0 ⇔ b2 + c2 – a2 < 0 ⇔ a2 > b2 + c2.
c) Góc A vuông ⇔ cos A = 0 ⇔ b2 + c2 – a2 = 0 ⇔ a2 = b2 + c2.
Đúng 0
Bình luận (0)
Cho a,b,c không âm. Chứng minh rằng :
a) a2 + b2 + c2 + 2abc + 2 > hoặc=ab +bc +ca +a+b+c
b)a2 + b2 +c2 +abc +4 > hoặc = 2(ab+bc+ca)
c) 3(a2 + b2 + c2) + abc +4 > hoặc =4 (ab+bc+ca)
d) 3(a2 + b2 + c2) + abc +80 > 4(ab+bc+ca) + 8(a+b+c)
Ngu kkkkkkkkkkkkkkkkkkkkkkkkkkkkkk
Cho a, b,c là độ dài ba cạnh tam giác. Chứng minh rằng: a/(a2 + bc) + 1/(b2+ ac) + s/(c2+ab) <= (a+b+c)/2abc
cho tam giác ABC, góc A=120 độ, AB=c, BC=a, AC=b. C/m: a2=b2+c2+bc
Cho tam giác ABC có BC = a, AC = b, AB = c và a2 = bc. Chứng minh rằng tam giác ABC đồng dạng với tam giác có độ dài các cạnh bằng độ dài ba đường cao của tam giác ABC.
Cho a, b, c là độ dài ba cạnh của một tam giác.
a) Chứng minh (b - c)2 < a2
b) Từ đó suy ra: a2 + b2 + c2 < 2(ab + bc + ca)
a) Vì a, b, c là độ dài 3 cạnh của một tam giác
⇒ a + c > b và a + b > c (Bất đẳng thức tam giác)
⇒ a + c – b > 0 và a + b – c > 0
Ta có: (b – c)2 < a2
⇔ a2 – (b – c)2 > 0
⇔ (a – (b – c))(a + (b – c)) > 0
⇔ (a – b + c).(a + b – c) > 0 (Luôn đúng vì a + c – b > 0 và a + b – c > 0).
Vậy ta có (b – c)2 < a2 (1) (đpcm)
b) Chứng minh tương tự phần a) ta có :
( a – b)2 < c2 (2)
(c – a)2 < b2 (3)
Cộng ba bất đẳng thức (1), (2), (3) ta có:
(b – c)2 + (c – a)2 + (a – b)2 < a2 + b2 + c2
⇒ b2 – 2bc + c2 + c2 – 2ca + a2 + a2 – 2ab + b2 < a2 + b2 + c2
⇒ 2(a2 + b2 + c2) – 2(ab + bc + ca) < a2 + b2 + c2
⇒ a2 + b2 + c2 < 2(ab + bc + ca) (đpcm).
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB=a, AC=b, AB=c. Biết b(b2- a2)=c(a2 -c2). Số đo của góc A bằng
A. 30 °
B. 60 °
C. 150 °
D. 120 °
Chứng minh rằng nếu a2+b2+c2-ab-bc-ac=0 thì a=b=c
Ta có :
\(\left(a-b-c\right)^2=a^2+b^2+c^2-2ab-2bc-2ac\)
mà theo đề bài \(a^2+b^2+c^2-ab-bc-ac=0\)
\(\Rightarrow\left(a-b-c\right)^2=-ab-bc-ac=0\)
\(\Rightarrow\left(a-b-c\right)^2=-\left(ab+bc+ac\right)=0\)
mà \(-\left(ab+bc+ac\right)\le0\)
\(\Rightarrow a=b=c=0\)
\(\Rightarrow dpcm\)
Đúng 4
Bình luận (0)