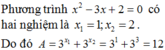Phương trình: \(^{x^2-x-3=0}\) có 2 nghiệm x1,x2. Tính giá trị \(^{x1^3x2+x2^3x1=21}\)
HN
Những câu hỏi liên quan
Gọi
x
1
,
x
2
là hai nghiệm của phương trình
x
2
-
3
x
+
2
0
. Tính giá trị của
A
3
x
1
+
3
x
2
A. A27. B. A28. C. A12. D. A9.
Đọc tiếp
Gọi x 1 , x 2 là hai nghiệm của phương trình x 2 - 3 x + 2 = 0 . Tính giá trị của A = 3 x 1 + 3 x 2
A. A=27.
B. A=28.
C. A=12.
D. A=9.
Biết rằng phương trình
3
x
2
+
1
.
25
x
-
1
3
25
có đúng hai nghiệm x1; x2. Tính giá trị của
P
3
x
1
+...
Đọc tiếp
Biết rằng phương trình 3 x 2 + 1 . 25 x - 1 = 3 25 có đúng hai nghiệm x1; x2. Tính giá trị của P = 3 x 1 + 3 x 2
A. P = 26 5
B. P = 26
C. P = 26
D. P = 26 25
Chọn A.
Phương trình ![]()
Lấy logarit cơ số 3 hai vế của (*), ta được ![]()
![]()
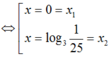
Suy ra 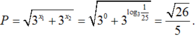
Đúng 0
Bình luận (0)
Bài 3: Cho phương trình 3x2 –2x–2=0 có hai nghiệm x1 , x2 . Hãy tính giá trị của biểu thức: D=x1/x2-1 + x2/x1-1
Cho phương trình x^2 -4x+m-5=0 tìm các giá trị m để phương trình có 2 nghiệm phân biệt x1,x2 thoã mãn(x1-1).(x2^2-3x2+m-6)=-3
=>(x1-1)[x2^2-x2(x1+x2-1)+x1x2+1]=-3
=>(x1-1)[-x1x2+x2+x1x2+1]=-3
=>(x1-1)(x2+1)=-3
=>x1x2+(x1-x2)-1=-3
=>(x1-x2)=-3+1-x1x2=-2-m+5=-m+3
=>(x1+x2)^2-4x1x2=m^2-6m+9
=>4^2-4(m-5)=m^2-6m+9
=>4m-20=16-m^2+6m-9=-m^2+6m+7
=>4m-20+m^2-6m-7=0
=>m^2-2m-27=0
=>\(m=1\pm2\sqrt{7}\)
Đúng 0
Bình luận (0)
Cho phương trình: 3x2 + 5x – 1 = 0 (1). Gọi x1 , x2 là hai nghiệm (nều
có) của phương trình (1). Không tìm x1 , x2 hãy tính K = (3x1 – 1)(3x2 – 1) + 3
Ta có: \(\Delta=5^2-5.3.1=25-12=13>0\)
Suy ra pt luôn có 2 nghiệm phân biệt
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=-5\\x_1x_2=-1\end{matrix}\right.\)
\(K=\left(3x_1-1\right)\left(3x_2-1\right)+3\\ =3x_1x_2-3x_2-3x_1+1+3=3.\left(-1\right)-3\left(x_1+x_2\right)+4\\ =-3+4-3\left(-5\right)\\ =1+15\\ =16\)
Đúng 0
Bình luận (1)
\(\Delta=25-4\left(-1\right).3=25+12=37>0\)
vậy pt luôn có 2 nghiệm pb
Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{5}{3}\\x_1x_2=-\dfrac{1}{3}\end{matrix}\right.\)
Ta có \(K=9x_1x_2-3\left(x_1+x_2\right)+4\)
Thay vào ta được \(K=9\left(-\dfrac{1}{3}\right)-3\left(-\dfrac{5}{3}\right)+4=-3+5+4=6\)
Đúng 0
Bình luận (1)
Cho phương trình x2+ 2(m − 1)x − 6m − 7 = 0 (1) (m là tham số).
a) Chứng minh rằng với mọi giá trị của m thì phương trình (1) luôn có hai nghiệm phân biệt.
b) Gọi x1, x2là hai nghiệm của phương trình (1). Tìm các giá trị của m thỏa x1(x1+3/3x2)+x2(x2+3/2x1)=15
các bạn ai biết thì chỉ giúp mình với ạ
\(x^{2^{ }}+2\left(m-1\right)x-6m-7=0\left(1\right)\)
a) \(Dental=\left[2\left(m-1\right)\right]^2-4\cdot1\cdot\left(-6m-7\right)\)
\(< =>4\cdot\left(m^2-2m+1\right)+24m+28\)
\(< =>4m^2-8m+4+24m+28\)
\(< =>4m^2+16m+32\)
\(< =>\left(2m+4\right)^2+16>0\) với mọi m
Vậy phương (1) luôn có 2 nghiệm phân biệt với mọi m
b) Theo định lí vi ét ta có:
x1+x2= \(\dfrac{-2\left(m-1\right)}{1}=-2m+1\)
x1x2= \(-6m-7\)
Đúng 0
Bình luận (0)
quy đồng
khử mẫu
tách sao cho có tích và tổng
thay x1x2 x1+x2
kết luận
mặt xấu vl . . .![]()
Đúng 0
Bình luận (0)
Cho phương trình x² – 2(m – 1)x + m² – 3m = 0. Tìm giá trị của m để phương trình có 2 nghiệm phân biệt x1, x2 thỏa mãn x2 + 3x1 = –2. Giups với mn ơi !!!
Cho phương trình: x²+2mx-3=0
Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt x1;x2 thỏa mãn: x1²+x2²+3x1.x2=1
=>(x1+x2)^2+x1x2=1
=>(-2m)^2+(-3)=1
=>4m^2=4
=>m=-1 hoặc m=1
Đúng 0
Bình luận (0)
Do a = 1 và c = -3
⇒ a và c trái dấu
⇒ Phương trình luôn có hai nghiệm phân biệt
Theo Viét, ta có:
x₁ + x₂ = -2m
x₁x₂ = -3
Lại có:
x₁² + x₂² + 3x₁x₂ = 1
⇔ x₁² + 2x₁x₂ + x₂² + x₁x₂ = 1
⇔ (x₁ + x₂)² + x₁x₂ = 1
⇔ (-2m)² - 3 = 1
⇔ 4m² = 4
⇔ m² = 1
⇔ m = -1 hoặc m = 1
Vậy m = -1; m = 1 thì phương trình đã cho có hai nghiệm phân biệt x₁, x₂ thỏa mãn: x₁² + x₂² + 3x₁x₂ = 1
Đúng 0
Bình luận (0)
Nếu phương trình sau:x^2-2x-1=0 có 2 nghiệm x1,x2(x1<x2) thì hãy tính giá trị các đại lượng sau mà ko giải PT(bài này làm theo định lí Vi-et)
1.((x1^2+2)/x1)+((x2^2+2)/x2)
2.(x2/(x2^2-3))+(x1/(x1^2-3))
3.(x1^2/(x1.x2^2-1))+(x2^2/(x1^2.x2-1))
4.(x1/(3.x1.x2^2-1)+(x2/3.x1^2.x2-1)
5.(1/x1)-(1/x2)
6.(x1/(x2-1))+(x2/(x1-1))
7.((3x1-7)/x2)-((3x2-7)/x1)
Mọi người giúp mình với