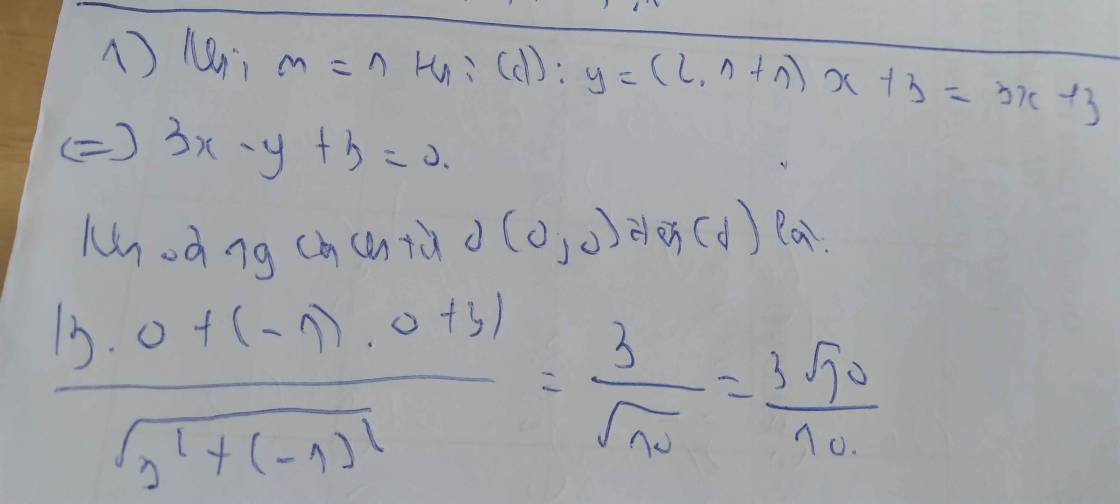Cho đường thẳng (d): (y=(2m+1)x-2) với m là tham số và (m\ne-\frac{1}{2}.) Khoảng cách từ (A(-2;1)) đến đường thẳng d được tính theo công thức:
[\sqrt{(-2-(2m+1)(-2))^2+(1-(2m+1)(-2))^2}]
[\sqrt{(16m^2+20m+4)^2+(24m+4)^2}]
[\sqrt{256m^4+640m^3+320m^2+576m^2+960m+16}]
[\sqrt{256m^4+1216m^3+1536m^2+960m+16}]
[\sqrt{16m^2(16m^2+79m+96)+4(16m^2+79m+96)}]
[\sqrt{(4m+7)^2(4m+16)}]
Theo đề bài, khoảng cách này bằng (\frac{1}{\sqrt{2}}.) Do đó, ta có phương trình:
[\sqrt{(4m+7)^2(4m+16)}=\frac{1}{\sqrt{2}}]
Từ đây, ta được phương trình bậc hai:
[(4m+7)^2(4m+16)=1 ]
Giải phương trình này, ta được hai nghiệm:
[m=-\frac{3}{2}\pm\frac{\sqrt{3}}{2} ]
Do (m\ne-\frac{1}{2},) ta có nghiệm duy nhất là:
[m=-\frac{3}{2}+\frac{\sqrt{3}}{2}=\frac{5}{7} ]
Vậy, tổng các giá trị của m thỏa mãn bài toán là [\frac{5}{7}.]