vẽ hình ạ
H24
Những câu hỏi liên quan
Bài 6: Cho hình vẽ: Biết . HEF = 120 Ta có, (vẽ hình giúp e ạ và vẽ hình câu c đi ạ)c) Vẽ Hm và En lần lượt là tia phân giác của GHE và HEF. Chứng minh Nm // En
Xem chi tiết

Giúp mình với ạ (bài hình vẽ hình giúp mình ạ)
\(3x=4z\Rightarrow\dfrac{x}{4}=\dfrac{z}{3}\); \(\dfrac{x}{5}=\dfrac{y}{6}\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{z}{15}=\dfrac{y}{24}\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{z}{15}=\dfrac{y}{24}=\dfrac{x-y+z}{20-24+15}=\dfrac{121}{11}=11\)
\(\Rightarrow x=20.11=220;z=15.11=165;y=264\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
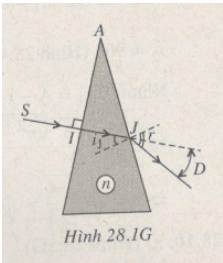
Giúp e câu 9 10 đi ạ scan vẽ hình thì vẽ luôn ạ
Câu 9.
Tại điểm \(I\): \(i=r=0\)
Tia sáng truyền thẳng vào lăng kính.
Tại điểm J có \(i_J=30^o\)
Theo định luật khúc xạ ánh sáng:
\(sinr=nsini_J=1,5\cdot sin30^o=\dfrac{3}{4}\Rightarrow r=arcsin\dfrac{3}{4}\)
Góc lệch:
\(D=r-i_J=arcsin\dfrac{3}{4}-30^o\approx18,6^o\)
Chọn B.
Hình vẽ tham khảo sgk lí 11!!!
Đúng 1
Bình luận (0)
Hãy vẽ lại bản vẽ hình chiếu đứng, hình chiếu cạnh, hình chiếu = của hình chóp nón.
mình đang gấp ạ!!!
Giúp mik với ạ!!! Vẽ hình nx ạ
Đề bài khó nhìn quá bạn ơi
Đúng 0
Bình luận (0)
cho hình vẽ biết BH = căn 2 cm, CH= căn 8 cm . tính diện tích tam giác ABC ( vẽ giúp em hình với ạ)(em đang cần gấp lắm ạ)
Bài là tam giác vuông hả bạn?
Ta có : BC = BH + CH = \(\sqrt{2}+\sqrt{8}=3\sqrt{2}\)
Xét △ ABC vuông tại A, đường cao AH có:
\(AB^2\)=BH.BC ( hệ thức lượng trong tam giác vuông)
=> \(AB^2=\sqrt{2}.3\sqrt{2}=6\)
=> \(AB=\sqrt{6}\)
\(AC^2=BC.HC\)
=> \(AC^2=\sqrt{8}.3\sqrt{2}=12\)
=>\(AC=2\sqrt{3}\)
\(S_{ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.\sqrt{6}.2\sqrt{6}=3\sqrt{2}\left(cm^2\right)\)
Đúng 1
Bình luận (0)
Mọi người ơi cho em hỏi là mình vẽ 3 hình chiếu đứng, bằng, cạch có cần đo hay không ạ😥 hay vẽ to hay nhỏ tùy theo sở thích của mình ạ (các hình đều nhau ạ)
Mong mn giúp ạ,vẽ hình nx ạ. :3
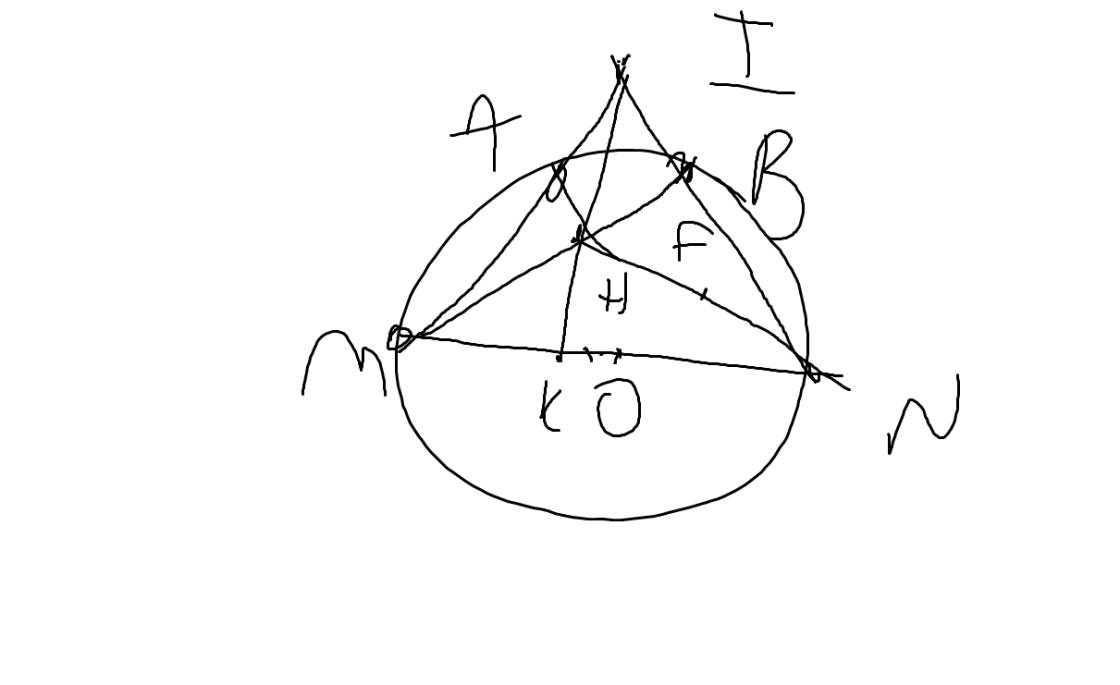
a: Xét (O) có
ΔMAN nội tiếp
MN là đường kính
Do đó: ΔMAN vuông tại A
=>NA\(\perp\)IM
Xét (O) có
ΔNBM nội tiếp
NM là đường kính
Do đó: ΔNBM vuông tại B
=>MB\(\perp\)NI
b: Xét ΔIMN có
MB,NA là đường cao
MB cắt NA tại H
Do đó: H là trực tâm
=>IH\(\perp\)MN tại K
Xét tứ giác BHKN có
\(\widehat{HBN}+\widehat{HKN}=90^0+90^0=180^0\)
=>BHKN nội tiếp đường tròn đường kính HN
tâm F là trung điểm của HN
Đúng 3
Bình luận (0)
 vẽ hình giúp e ạ có gì giải ra ạ em cảm ơn ạ=))
vẽ hình giúp e ạ có gì giải ra ạ em cảm ơn ạ=))
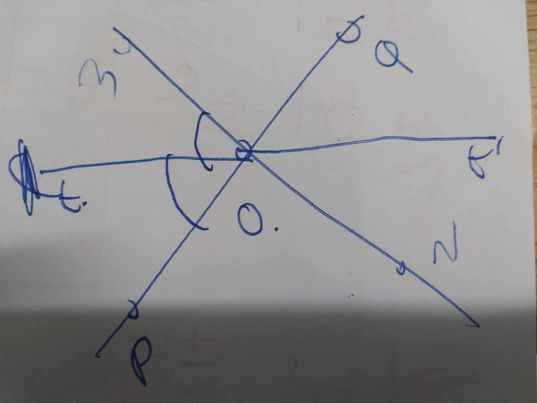
10: Chọn B
Ot là phân giác của \(\widehat{MOP}\)
=>\(\widehat{MOP}=2\cdot\widehat{tOP}\)
\(\widehat{MOP}=\widehat{NOQ}\)
=>\(\widehat{NOQ}=2\cdot\widehat{tOP}\)
mà \(\widehat{tOP}=\widehat{t'OQ}\)(hai góc đối đỉnh)
nên \(\widehat{NOQ}=2\cdot\widehat{t'OQ}\)
=>Ot' là phân giác của góc NOQ
11:
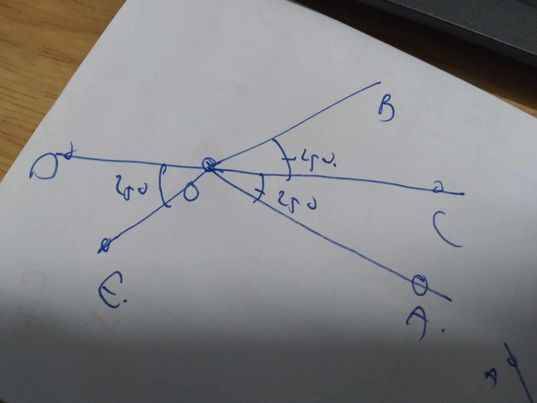
OC là phân giác của góc AOB
=>\(\widehat{AOC}=\widehat{BOC}=\dfrac{50^0}{2}=25^0\)
\(\widehat{DOE}=\widehat{BOC}\left(=25^0\right)\)
=>\(\widehat{DOE}+\widehat{DOB}=180^0\)
=>OB và OE là hai tia đối nhau
=>Hai góc đối đỉnh là \(\widehat{BOC};\widehat{DOE}\)
=>Chọn D
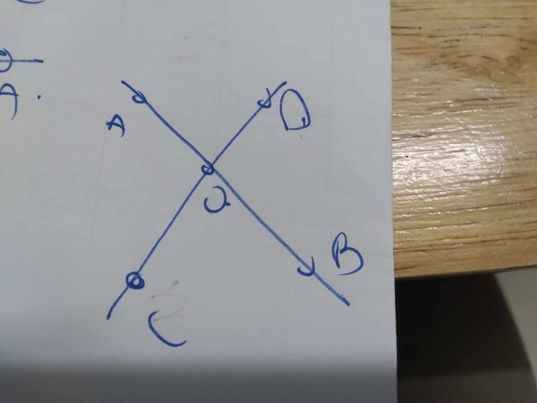
12:
\(\widehat{AOC}+\widehat{AOD}=180^0\)
\(\widehat{AOC}-\widehat{AOD}=50^0\)
Do đó: \(\widehat{AOC}=\dfrac{180^0+50^0}{2}=115^0;\widehat{AOD}=115^0-50^0=65^0\)
=>\(\widehat{BOC}=\widehat{AOD}=65^0\)
=>Chọn B
Đúng 0
Bình luận (0)
 vẽ hình ạ làm chi tiết với ạ nhanh gấp
vẽ hình ạ làm chi tiết với ạ nhanh gấp
Bài 1:
a,b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vừa là đường cao, vừa là phân giác
=>góc BAM=góc CAM và AM vuông góc với BC
c: Xét ΔEBC có
EM vừa là đường cao, vừa là trung tuyến
nên ΔEBC cân tại E
d: Xét ΔKCB có
CE là trung tuyến
CE=KB/2
Do đó: ΔKCB vuông tại C
=>KC//AE
Đúng 1
Bình luận (0)






