bài 21 trang 19 sgk 9 tập 2
(nguyễn lê phước thịnh giúp với)
AD
Những câu hỏi liên quan
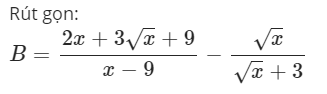
@Nguyễn Lê Phước Thịnh: NÉ HỘ
\(B=\dfrac{2x+3\sqrt{x}+9}{x-9}-\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
\(\Rightarrow B=\dfrac{2x+3\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(\Rightarrow B=\dfrac{2x+3\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{x-3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(\Rightarrow B=\dfrac{2x+3\sqrt{x}+9-x+3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(\Rightarrow B=\dfrac{x+6\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(\Rightarrow B=\dfrac{\left(\sqrt{x}+3\right)^2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(\Rightarrow B=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}\)
Đúng 3
Bình luận (2)
\(\dfrac{2x+3\sqrt{x}+9-\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\left(\sqrt{x}+3\right)^2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}\)
Đúng 0
Bình luận (1)
\(B=\dfrac{2x+3\sqrt{x}+9-x+3\sqrt{x}}{x-9}=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}\)
Đúng 3
Bình luận (0)
Giúp em câu b và câu d ạ!
Em cũng cảm ơn anh NGUYỄN LÊ PHƯỚC THỊNH đã trả lời câu a và câu c
b) Ta có: \(\left(-\dfrac{1}{2}\right)^2\cdot2\dfrac{6}{7}-\dfrac{14}{15}:2\dfrac{1}{3}+\left(-1.21\right)^0\)
\(=\dfrac{1}{4}\cdot\dfrac{20}{7}-\dfrac{14}{15}:\dfrac{7}{3}+1\)
\(=\dfrac{5}{7}-\dfrac{14}{15}\cdot\dfrac{3}{7}+1\)
\(=\dfrac{5}{7}-\dfrac{2}{5}+1\)
\(=\dfrac{25-14-35}{35}=\dfrac{-24}{35}\)
Đúng 1
Bình luận (1)
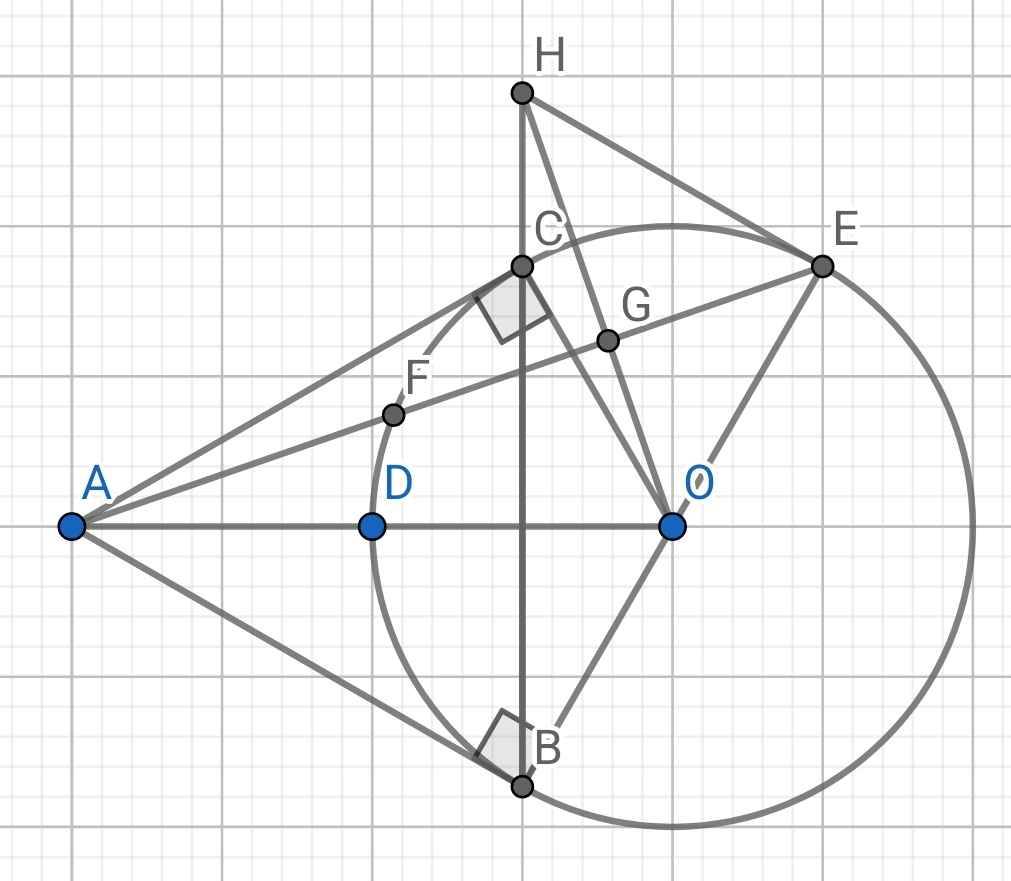
BẠN NGUYỄN LÊ PHƯỚC THỊNH VẼ LẠI MÌNH HỘ CÁI HÌNH VỪA NÃY VỚI HÌNH VỪA NÃY KHÓ NHÌN LẮM Cho đường tròn (O) bán kính R 2 cm. Điểm A nằm ngoài đường tròn. Từ A vẽ các tiếp tuyến AB,AC với đường tròn (B,C là các tiếp điểm). AO cắt BC tại D. a) Cmr 4 điểm A,B,O,C cùng thuộc 1 đường tròn và OA là trung trực của BC b) Vẽ đk BE của đường tròn (O), AE cắt đt (O) tại đ...
Đọc tiếp
BẠN NGUYỄN LÊ PHƯỚC THỊNH VẼ LẠI MÌNH HỘ CÁI HÌNH VỪA NÃY VỚI HÌNH VỪA NÃY KHÓ NHÌN LẮM
Cho đường tròn (O) bán kính R = 2 cm. Điểm A nằm ngoài đường tròn. Từ A vẽ các tiếp tuyến AB,AC với đường tròn (B,C là các tiếp điểm). AO cắt BC tại D. a) Cmr 4 điểm A,B,O,C cùng thuộc 1 đường tròn và OA là trung trực của BC b) Vẽ đk BE của đường tròn (O), AE cắt đt (O) tại điểm thứ hai F. Gọi G là trung điểm của EF. Đt OG cắt đt BC tại H. Tính tích OA.OD và cm OA.OD=OG.OH c) CM EH là tiếp tuyến của đt (O)
Minigame ôn luyện cho những bạn vào vòng 2 gồm 2 bài (do Nguyễn Lê Phước Thịnh tài trợ)những bạn làm được hết 2 bài sẽ được thưởng 5 gp còn các bạn làm được 1 bài 2 gb :bài 1: Nobita và cuộc chiến giữa các hành tinh:Nobita là 1 đứa trẻ vô cùng hậu đậu, vụng về, đôi lúc khá đãng trí nhưng cậu lại có khả năng bắn súng vô cùng thiện xạ. Vào 1 ngày đẹp trời, Doraemon rủ cậu chơi 1 trò chơi đến từ tương lai. Trò chơi đưa Nobita đến 1 thế giới nơi đó cậu ta có thể trở thành 1 siêu anh hùng cứu thế giớ...
Đọc tiếp
Minigame ôn luyện cho những bạn vào vòng 2 gồm 2 bài (do Nguyễn Lê Phước Thịnh tài trợ)
những bạn làm được hết 2 bài sẽ được thưởng 5 gp còn các bạn làm được 1 bài 2 gb :
bài 1: Nobita và cuộc chiến giữa các hành tinh:
Nobita là 1 đứa trẻ vô cùng hậu đậu, vụng về, đôi lúc khá đãng trí nhưng cậu lại có khả năng bắn súng vô cùng thiện xạ. Vào 1 ngày đẹp trời, Doraemon rủ cậu chơi 1 trò chơi đến từ tương lai. Trò chơi đưa Nobita đến 1 thế giới nơi đó cậu ta có thể trở thành 1 siêu anh hùng cứu thế giới khỏi sự xâm lược của người ngoài hành tinh. Trò chơi có 101 màn, nhưng với tài năng xuất chúng của mình nobita đã vuợt 100 màn đầu tiên 1 cách rất dễ dàng. Nhưng đến màn cuối cùng, xung quanh bỗng nhiên xuất hiện rất nhiều UFO của kẻ thù. Bởi vì đây là màn cuối nên rất khó, các UFO có thể phân thân để gây nhiễu loạn cho nobita. Nếu có vô số đạn nobita sẽ dễ dàng vượt qua trò chơi này. Nhưng trò chơi chỉ cho Nobita 1 số lượng đạn nhất định tương ứng với số lượng các UFO cần tiêu diệt (Nếu bắn lung tung thì Nobia có thể mất đạn lãng phí, không tiêu diệt được hết kẻ thù và thua cuộc). Vì vậy Nobita cần phải bắn chính xác ko được trượt phát nào. Ngoài ra, các UFO còn có thể thay đổi độ cao theo thời gian. Trò chơi biết rằng dù Nobita rất giỏi bắn súng nhưng lại chưa dủ trình độ để nhận biết đâu là UFO chính, đâu là bản sao. Nên trò chơi phải cho Nobita một vài gợi ý để cậu ta có khả năng chiến thắng cao hơn. Ban đầu, trò chơi sẽ cung cấp vị trí, độ cao ban đầu của các UFO (cả chính, lẫn bản sao). Một lần, trò chơi sẽ cung cấp cho Nobita 1 thông tin của kẻ thù:
1 u v: là UFO uu thay đổi độ cao thành vv.
2 u v val: UFO cần tiêu diệt chính sẽ nằm ở vị trí nằm trong khoảng từ uu đến vv, gần bên trái nhất và đang bay ở độ cao thấp hơn hoặc bằng valval.
Tuy đã đưa ra nhưng gợi ý rất chi tiết như vậy nhưng Nobita vẫn chưa thể giải được gợi ý và nhận biết được đâu ra UFO của kẻ thù. Chính vì vậy cậu mới nhờ đến các lập trình viên tương lai. Với tài năng xuất chúng của các lập trình viên trên LQDOJ, các bạn hãy dùng trí thông minh của mình để giúp Nobita nhé. Nobita xin cảm ơn các bạn bằng 1 nghìn lời cảm ơn!!!!!!!!!!!
Input:
Dòng đầu chứa hai số nguyên n,qn,q - là số lượng UFO ban đầu, số lượng gợi ý. (1≤n≤105,1≤q≤106)(1≤n≤105,1≤q≤106)
Dòng tiếp theo gồm a1,a2,a3,...,ana1,a2,a3,...,an là độ cao ban đầu của các UFO. (0≤ai≤109)(0≤ai≤109)
qq dòng tiếp theo - là nội dung các gợi ý cần giải quyết:
1 u v (1≤u≤n,0≤v≤109)(1≤u≤n,0≤v≤109)
2 u v val (1≤u≤v≤n,0≤val≤109)(1≤u≤v≤n,0≤val≤109)
Output:
Với mỗi gợi ý 2 cần trả lời vị trí UFO Nobita cần tiêu diệt:
Nếu có vị trí tồn tại, in ra vị trí đó.
Nếu không, in ra "Skip" để Nobita bỏ qua, ko bắn.
Test ví dụ:
Input:
| 5 7 5 3 2 5 2 2 2 4 3 1 2 4 2 1 5 2 2 1 2 1 1 3 9 1 5 7 2 1 5 4 |
output:
| 2 3 Skip 2 |
bài 2: K-Amazing Numbers
Cho mảng aa gồm nn số nguyên dương
Gọi qkqk là số nguyên nhỏ nhất có mặt ở tất cả các đoạn con (gồm các phần tử liên tiếp) có kích thước là kk.
Nếu không tồn tại qkqk thỏa mãn điều trên thì qk=−1qk=−1.
Nhiệm vụ của chúng ta là in ra tất cả các giá trị qiqi với 1≤i≤n1≤i≤n.
Input:
Dòng thứ nhất chứa số nguyên t(1≤t≤1000)t(1≤t≤1000) - Thể hiện số lượng testcase
Tiếp theo là tt block, mỗi block có dạng như sau:
Dòng thứ nhất chứa số nguyên n(1≤n≤3.105)n(1≤n≤3.105)
Dòng thứ hai chứa số nguyên a1,a2,...,ana1,a2,...,an với 1≤ai≤n1≤ai≤n
(Biết rằng: Tổng các giá trị của nn ở tất cả testcase không quá 3.1053.105)
Output:
ứng với mỗi testcase ,in ra các giá trị q1,q2,...,qnq1,q2,...,qn tương ứng
Ví dụ:
Input:
| 3 5 1 2 3 4 5 5 4 4 4 4 2 6 1 3 1 5 3 1 |
output
-1 -1 3 2 1
|
Bài 34: Cho biểu thức: A(b^2+c^2-a^2)^2-4b^2c^2(đố Nguyễn Lê Phước Thịnh đó :_)a, Phân tích A thành nhân tửb, Chứng minh rằng: Nếu a, b, c là độ dài các cạnh của 1 tam giác thì A 0
Đọc tiếp
Bài 34: Cho biểu thức: A=(b^2+c^2-a^2)^2-4b^2c^2(đố Nguyễn Lê Phước Thịnh đó :_)
a, Phân tích A thành nhân tử
b, Chứng minh rằng: Nếu a, b, c là độ dài các cạnh của 1 tam giác thì A< 0
a: \(A=\left(b^2+c^2-a^2\right)^2-4b^2c^2\)
\(=\left(b^2+c^2-a^2\right)^2-\left(2bc\right)^2\)
\(=\left(b^2-2bc+c^2-a^2\right)\left(b^2+2bc+c^2-a^2\right)\)
\(=\left[\left(b+c\right)^2-a^2\right]\left[\left(b-c\right)^2-a^2\right]\)
\(=\left(b+c-a\right)\left(b+c+a\right)\left(b-c-a\right)\left(b-c+a\right)\)
b: a,b,c là độ dài 3 cạnh của 1 tam giác
=>b+c>a và a+b>c và a+c>b
=>b+c-a>0 và a+b-c>0 và a+c-b>0
=>b+c-a>0 và b-(c+a)<0 và a+b-c>0
=>(b+c-a)[b-(c+a)][a+b-c](a+b+c)<0
=>A<0
Đúng 2
Bình luận (0)
Bài 34: Cho biểu thức: A(b^2+c^2-a^2)^2-4b^2c^2(đố Nguyễn Lê Phước Thịnh đó :_)a, Phân tích A thành nhân tửb, Chứng minh rằng: Nếu a, b, c là độ dài các cạnh của 1 tam giác thì A 0
Đọc tiếp
Bài 34: Cho biểu thức: A=(b^2+c^2-a^2)^2-4b^2c^2(đố Nguyễn Lê Phước Thịnh đó :_)
a, Phân tích A thành nhân tử
b, Chứng minh rằng: Nếu a, b, c là độ dài các cạnh của 1 tam giác thì A< 0
mấy cụ làm gì mà viết phân số nhanh thế ;-;
doraemon2611,nợn, nguyễn lê phước thịnh.....và rất nhiều người không rảnh để viết :))
Xem thêm câu trả lời
Câu 2 (trang 19, SGK Ngữ Văn 10, tập hai)
Đề bài: Giữa tiếng đàn và mong ước của Nguyễn Trãi có liên hệ gì?
- Ước nguyện của tác giả và tình yêu nước, thương dân sâu sắc:
“Dễ có Ngu cầm đàn một tiếng
Dân giàu đủ, khắp đòi phương”
+ Ung dung, tự tại, không muốn vướng bận đến chuyện quan trường nhưng vẫn luôn nghĩ về dân, về nước.
→ Tác giả khao khát muốn đem tài trí của mình để cống hiến cho đất nước, cho dân tộc
+ Tác giả mong có cây đàn của vua Ngu Thuấn để hát ca mong muốn mang lại cuộc sống ấm no, sung túc, yên vui cho nhân dân muôn nơi.
→ Tấm lòng yêu thương nhân dân. Ước mong, khát vọng cao đẹp về một cuộc sống thái bình, hạnh phúc cho muôn dân
Đúng 0
Bình luận (0)
cái này cũng hỏi anh Nguyễn Lê Phước Thịnh luôn anh giúp giùm em với ,mai em kiểm tra rồicho một hình chữ nhật ABCD,cạnh AB bằng a,cạnh BCb.a,b là các số nguyên dương trong khoảng từ 1 đến 100.một điểm M chạy trong đoạn BC với BMX. X là số nguyên dương trong khoảng từ 0 đến b . Điểm N chạy trong đoạn CD với CNxtính giá trị lớn nhất và nhỏ nhất của diện tích tam giác AMN và X khi M,N lưu độngdòng đầu là diện tích lớn nhất của tam giác AMNdòng 2 là giá trị của x khi đódòng 3 là diện tích bé nhất c...
Đọc tiếp
cái này cũng hỏi anh Nguyễn Lê Phước Thịnh luôn anh giúp giùm em với ,mai em kiểm tra rồi
cho một hình chữ nhật ABCD,cạnh AB bằng a,cạnh BC=b.a,b là các số nguyên dương trong khoảng từ 1 đến 100.
một điểm M chạy trong đoạn BC với BM=X. X là số nguyên dương trong khoảng từ 0 đến b . Điểm N chạy trong đoạn CD với CN=x
tính giá trị lớn nhất và nhỏ nhất của diện tích tam giác AMN và X khi M,N lưu động
dòng đầu là diện tích lớn nhất của tam giác AMN
dòng 2 là giá trị của x khi đó
dòng 3 là diện tích bé nhất của tam giác AMN
dòng 4 là giá trị của x khi đó
vd:
nhập:10 6
in ra: 30.0
0
17.5
5