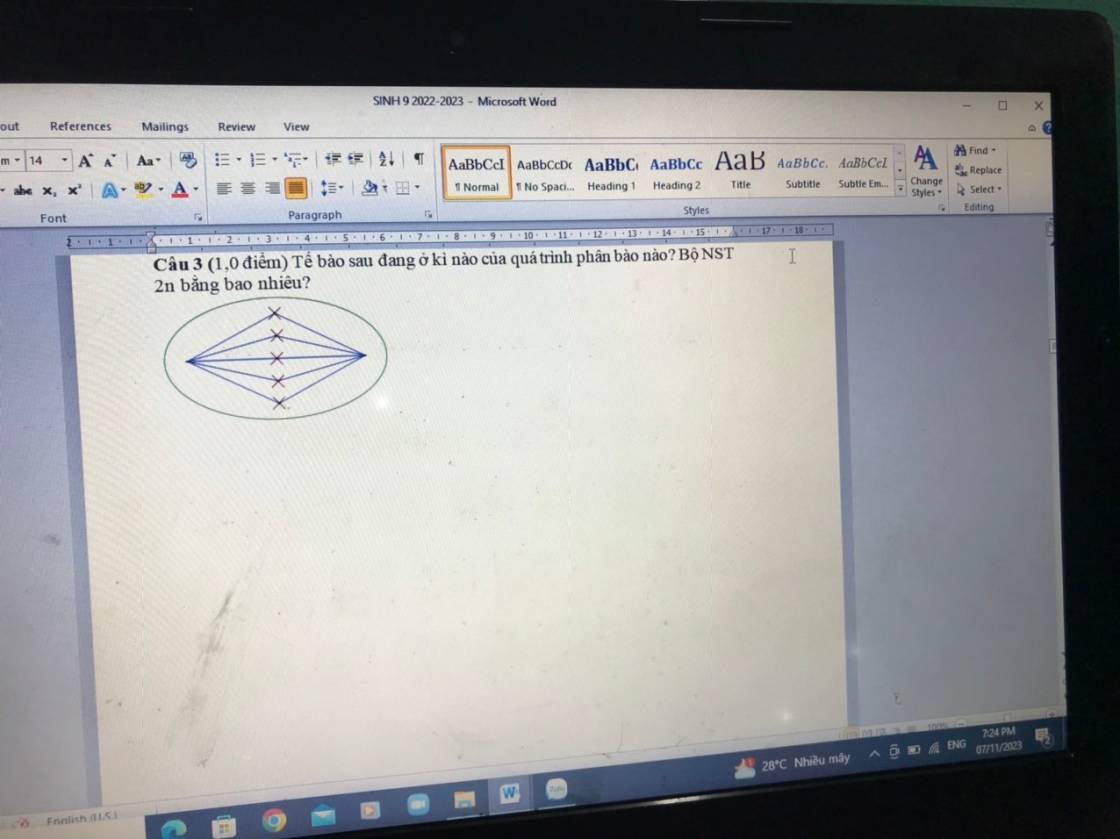
 mn giúp em 2 câu 3 với ạ,em cảm ơn
mn giúp em 2 câu 3 với ạ,em cảm ơn
LN
Những câu hỏi liên quan
giúp em bài 3 với ạ trừ câu c,e,j ạ ,em cảm ơn,em đang vội mong mn giúp đỡ
Bài 3:
\(a,=3x\left(y-4x+6y^2\right)\\ b,=5xy\left(x^2-6x+9\right)=5xy\left(x-3\right)^2\\ d,=\left(x+y\right)\left(x-12\right)\\ f,=2x\left(x-y\right)\left(5x-4y\right)\\ g,=\left(x-2\right)\left(x-2+3x\right)=\left(x-2\right)\left(4x-2\right)=2\left(x-2\right)\left(2x-1\right)\\ h,=x^2\left(1-5x\right)+3xy\left(5x-1\right)=x\left(1-5x\right)\left(x-3y\right)\\ i,=x\left(x-2\right)+4\left(x-2\right)=\left(x+4\right)\left(x-2\right)\\ j,=x^2-2x-3x+6=\left(x-2\right)\left(x-3\right)\\ k,=4x^2-12x+3x-9=\left(x-3\right)\left(4x+3\right)\\ l,=\left(x+5\right)^2-y^2=\left(x-y+5\right)\left(x+y+5\right)\\ m,=x^2-\left(2y-6\right)^2=\left(x-2y+6\right)\left(x+2y-6\right)\\ n,=\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24\\ =\left(x^2+5x+5\right)^2-1-24\\ =\left(x^2+5x+5\right)^2-25\\ =\left(x^2+5x\right)\left(x^2+5x+10\right)\\ =x\left(x+5\right)\left(x^2+5x+10\right)\)
Đúng 2
Bình luận (2)
Bài 3:
a)3xy-12x2+24xy2=3x(y-4x+8y2)
b)5x3y-30x2y+45xy=5xy(x2-6x+9)=5xy(x-6x+32)=5xy(x-3)2
d)x(x+y)-12x-12y=x(x+y)-(12x+12y)=x(x+y)-12(x+y)=(x+y)(x-12)
f)10x2(x-y)-8xy(x-y)=(x-y)(10x2-8xy)
g)(x-2)3+3x2-6x=(x-2)3+(3x2-6x)=(x-2)3+3x(x-2)=(x-2)[(x-2)+3x]=(x-2)(x-2+3x)=(x-2)(4x-2)
h)x2+15x2y-3xy-5x3=(x2-3xy)+(15x2y-5x3)=x(x-3y)+5x2(3y-x)=x(x-3y)-5x2(x-3y)=(x-3y)(x-5x2)
i)x2-2x-8+4x=(x2-2x)+(4x-8)=x(x-2)+4(x-2)=(x-2)(x+4)
k)4x2-9x-9=4x2+3x-12x-9=(4x2+3x)-(12x+9)=x(4x+3)-3(4x+3)=(4x+3)(x-3)
l)x2-y2+10x+25=(x2+10x+25)-y2=(x2+10x+52)-y2=(x+5)2-y2=[(x+5)+y][(x+5)-y]=(x+5+y)(x+5-y)
m)x2-4y2+24y-36=x2-(4y2-24y+36)=x2-[(2y)2-24y+62]=x2-(2y-6)2=[x+(2y-6)][x-(2y-6)]=(x+2y-6)(x-2y+6)
n)(không biết làm)
Đúng 0
Bình luận (0)
Mn giúp em với ạ em cần gấp mai đi học ạ em cảm ơn giúp em câu 1 ạ
\(=>Qthu1=0,2.340000=68000J\)
\(=>Qthu2=2100.0,2.20=8400J\)
\(=>Qtoa=2.4200.25=210000J\)
\(=>Qthu1+Qthu2< Qtoa\)=>đá nóng chảy hoàn toàn
\(=>0,2.2100.20+0,2.340000+0,2.4200.tcb=2.4200\left(25-tcb\right)\)
\(=>tcb=14,5^oC\)
Đúng 3
Bình luận (1)
Mn giúp em phần d câu 3 đề 1 với ạ , em đang cần gấp , em cảm ơn nhiều 
MN giúp em câu 2b với 4b với ạ , em cảm ơn nhiều lắm ạ
2b.
\(Q=\dfrac{cosx}{sinx}+\dfrac{sinx}{1+cosx}=\dfrac{cosx\left(1+cosx\right)+sin^2x}{sinx\left(1+cosx\right)}=\dfrac{cosx+cos^2x+sin^2x}{sinx\left(1+cosx\right)}=\dfrac{cosx+1}{sinx\left(1+cosx\right)}=\dfrac{1}{sinx}\)
4b.
\(\Delta\) có 1 vtpt là (3;-4)
Gọi d là đường thẳng qua M và vuông góc \(\Delta\Rightarrow d\) nhận (4;3) là 1 vtpt
Phương trình d:
\(4\left(x-4\right)+3\left(y+2\right)=0\Leftrightarrow4x+3y-10=0\)
H là giao điểm d và \(\Delta\) nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}3x-4y+5=0\\4x+3y-10=0\end{matrix}\right.\) \(\Rightarrow H\left(1;2\right)\)
Đúng 1
Bình luận (0)
mn giải giúp em câu 15 với ạ, em cảm ơn

Mn làm giúp em 3 câu đầu vs ạ . Em cảm ơn 
Ai làm giúp em câu 3 và 4 này với được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.
Dạ mong mn giúp em giải mấy câu với ạ, em đng cần gấp để học tuần sau thi giữa kỳ 1 ạ,em cảm ơn mn nhiều ạ 



36B
37C
38D
39B
40D
41A
42B
43B
44A
45B
46B
47A
48C
50B
51B
52B
53D
54C
55D
56C
Đúng 1
Bình luận (0)
 mn ơi! giúp em câu này với em cần gấp lắm! em cảm ơn mọi người ạ=:>
mn ơi! giúp em câu này với em cần gấp lắm! em cảm ơn mọi người ạ=:>
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó:ΔABM=ΔACM
b: ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: BC=6cm
nên BM=3cm
=>AM=4cm
d: Xét ΔABC cân tại A có AM là đường cao
nên AM là phân giác của góc BAC
Xét ΔABC có
AM là đường phân giác
BI là đường phân giác
AM cắt BI tại I
Do đó: CI là tia phân giác của góc ACB
Đúng 4
Bình luận (2)
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó:ΔABM=ΔACM
b: ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: BC=6cm
nên BM=3cm
=>AM=4cm
d: Xét ΔABC cân tại A có AM là đường cao
nên AM là phân giác của góc BAC
Xét ΔABC có
AM là đường phân giác
BI là đường phân giác
AM cắt BI tại I
Do đó: CI là tia phân giác của góc ACB
Đúng 0
Bình luận (1)
a) Xét 2 tam giác ABM và tam giác ACM:
Có: góc ABM= góc ACM (tam giác ABC cân) ; BM=MC và AM chung
==>tam giác ABM=tam giác ACM
b)Trong một tam giác cân, đường trung trực ứng với cạnh đáy cũng đồng thời là đường phân giác
Xét tam giác ABC cân và có AM là trung trực (M là tđ BC)
==> AM là đường cao Tam giác ABC
==> AM vuông góc BC
c)Có M là trung điểm BC
==> BM=MC=1/2 BC
Mà BC =6cm
==> BM=3cm
Áp dụng định lý Pitago trong tam giác ABM : Góc AMB=90 độ
==> AM^2+BM^2=AB^2
AM^2+3^2=5^2
==> AM =4cm
d) Xét tam giác IMB và tam giác IMC : góc IMC=Góc IMB(=90 độ)
IM chung;BM=MC(gt)
==> Tam Giác IMB=Tam giác IMC (c.g.c)
==> góc IBM=góc ICM
Mà góc ABM=Góc ACM (gt)
==> góc ABI+IBM=góc ACI+ICM
mà góc IBM=góc ICM
==> góc ABI= góc ACI
từ đó ==> góc ACM=ICM
==> CI là phân giác góc C
Bài của chị chỉ dùng tham khảo thôi nha ,có chỗ nào không hiểu thì nhắn lại nha!
Chúc em học tốt *\(^o^)/*
Đúng 1
Bình luận (1)





