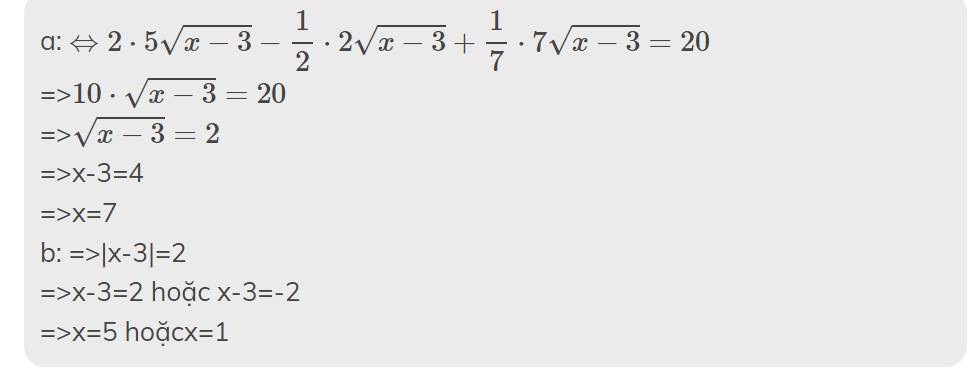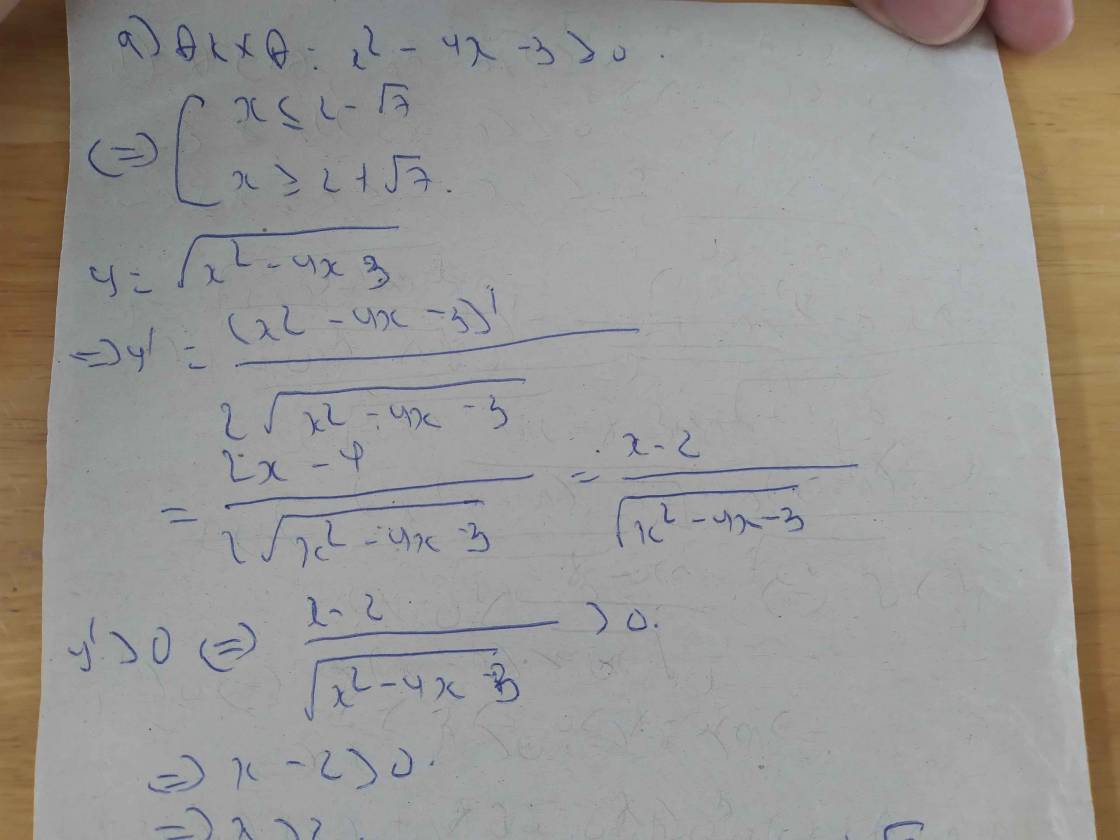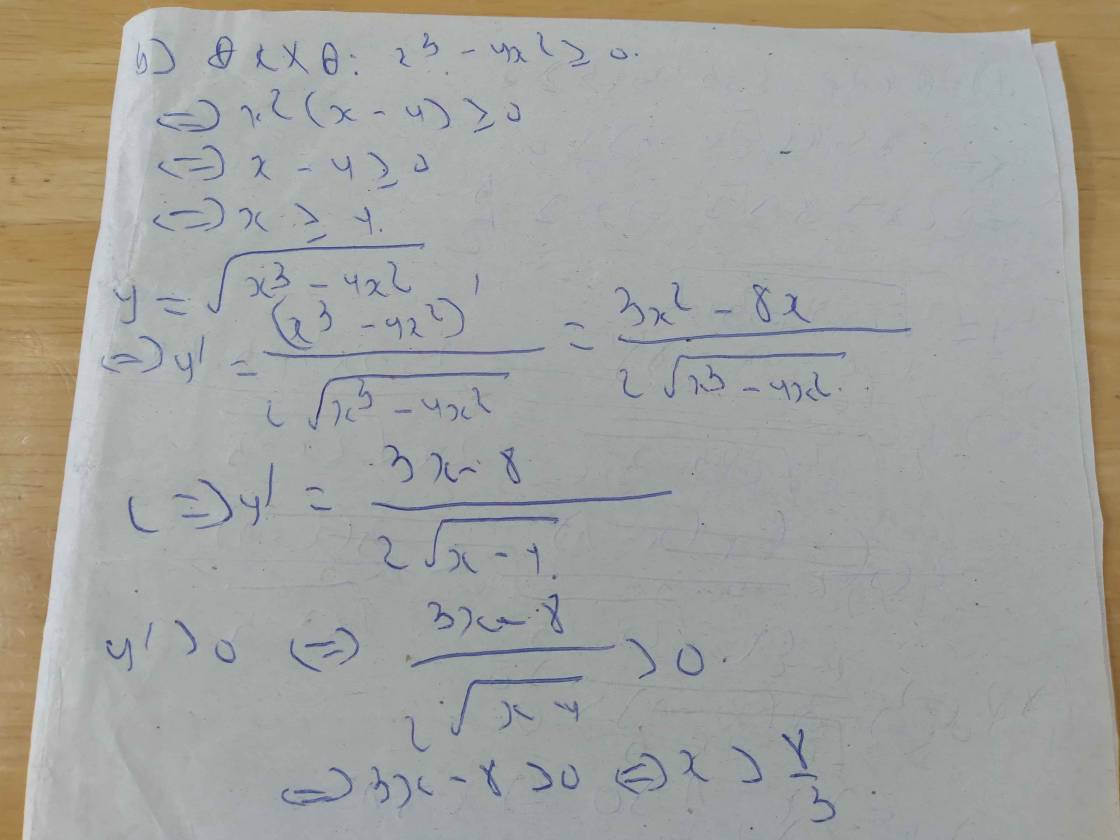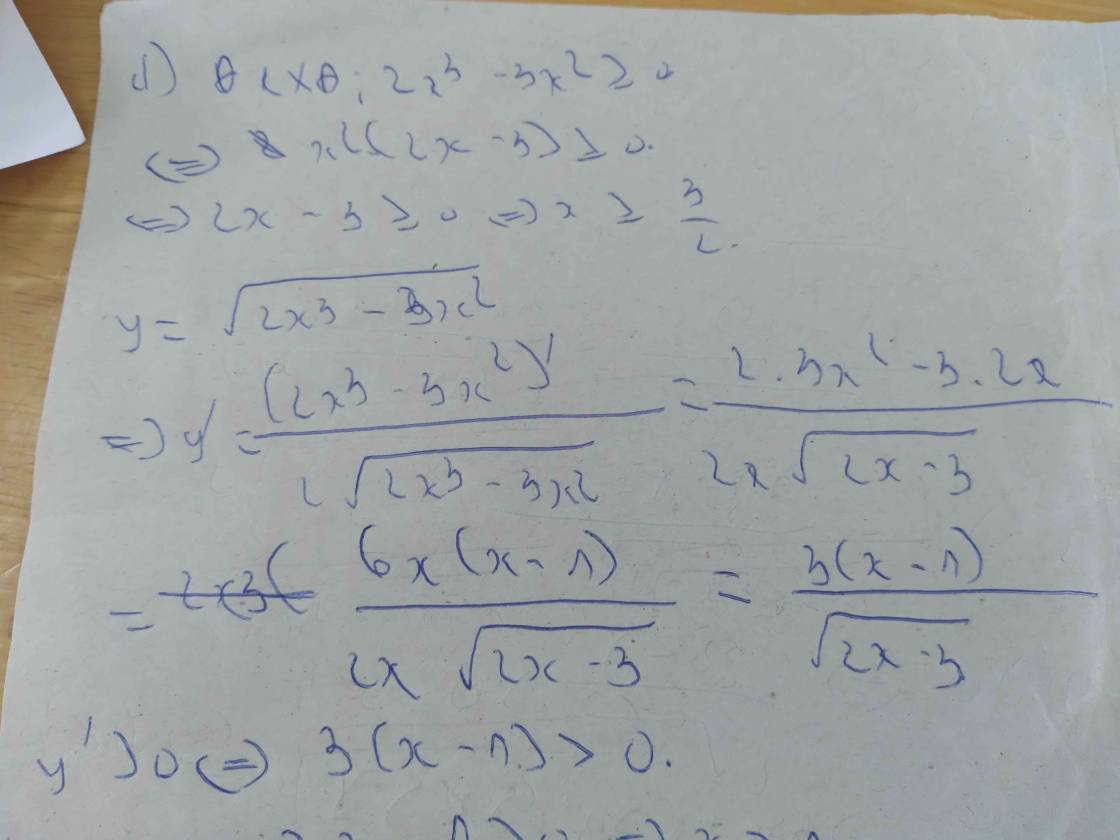\(7\sqrt{x-3}-2\sqrt{4x-12}=12\)
H24
Những câu hỏi liên quan
tìm x biết a,\(\sqrt{x^2-4x+4}=7\) b,\(\sqrt{4x+12}-3\sqrt{x+3}+\dfrac{4}{3}\sqrt{9x+27}=6\)
a: ĐKXĐ: \(x\in R\)
\(\sqrt{x^2-4x+4}=7\)
=>\(\sqrt{\left(x-2\right)^2}=7\)
=>|x-2|=7
=>\(\left[{}\begin{matrix}x-2=7\\x-2=-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=9\\x=-5\end{matrix}\right.\)
b: ĐKXĐ: x>=-3
\(\sqrt{4x+12}-3\sqrt{x+3}+\dfrac{4}{3}\cdot\sqrt{9x+27}=6\)
=>\(2\sqrt{x+3}-3\sqrt{x+3}+\dfrac{4}{3}\cdot3\sqrt{x+3}=6\)
=>\(3\sqrt{x+3}=6\)
=>\(\sqrt{x+3}=2\)
=>x+3=4
=>x=1(nhận)
Đúng 3
Bình luận (0)
a) \(\sqrt{4x^2-9}=2\sqrt{x+3}\)
b) \(\sqrt{4x+20}+3\sqrt{\dfrac{x-5}{9}}-\dfrac{1}{3}\sqrt{9x-45}=4\)
c) \(\dfrac{2}{3}\sqrt{9x-9}-\dfrac{1}{4}\sqrt{16x-16}+27\sqrt{\dfrac{x-1}{81}}=4\)
d)\(5\sqrt{\dfrac{9x-27}{25}}-7\sqrt{\dfrac{4x-12}{9}}-7\sqrt{x^2-9}+18\sqrt{\dfrac{9x^2-81}{81}}=0\)
\(a) \sqrt{4x^2− 9} = 2\sqrt{x + 3}\)
\(ĐK:x\ge\dfrac{3}{2}\)
\(pt\Leftrightarrow4x^2-9=4\left(x+3\right)\)
\(\Leftrightarrow4x^2-9=4x+12\)
\(\Leftrightarrow4x^2-4x-21=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1-\sqrt{22}}{2}\left(l\right)\\x=\dfrac{1+\sqrt{22}}{2}\left(tm\right)\end{matrix}\right.\)
\(b)\sqrt{4x-20}+3.\sqrt{\dfrac{x-5}{9}}-\dfrac{1}{3}\sqrt{9x-45}=4\)
\(ĐK:x\ge5\)
\(pt\Leftrightarrow2\sqrt{x-5}+\sqrt{x-5}-\sqrt{x-5}=4\)
\(\Leftrightarrow2\sqrt{x-5}=4\Leftrightarrow\sqrt{x-5}=2\)
\(\Leftrightarrow x-5=4\Leftrightarrow x=9\left(tm\right)\)
Đúng 1
Bình luận (0)
\(c)\dfrac{2}{3}\sqrt{9x-9}-\dfrac{1}{4}\sqrt{16x-16}+27.\sqrt{\dfrac{x-1}{81}}=4\)
ĐK:x>=1
\(pt\Leftrightarrow2\sqrt{x-1}-\sqrt{x-1}+3\sqrt{x-1}=4\)
\(\Leftrightarrow4\sqrt{x-1}=4\Leftrightarrow\sqrt{x-1}=1\)
\(\Leftrightarrow x-1=1\Leftrightarrow x=2\left(tm\right)\)
\(d)5\sqrt{\dfrac{9x-27}{25}}-7\sqrt{\dfrac{4x-12}{9}}-7\sqrt{x^2-9}+18\sqrt{\dfrac{9x^2-81}{81}}=0\)
\(ĐK:x\ge3\)
\(pt\Leftrightarrow3\sqrt{x-3}-\dfrac{14}{3}\sqrt{x-3}-7\sqrt{x^2-9}+6\sqrt{x^2-9}=0\)
\(\Leftrightarrow-\dfrac{5}{3}\sqrt{x-3}-\sqrt{x^2-9}=0\Leftrightarrow\dfrac{5}{3}\sqrt{x-3}+\sqrt{x^2-9}=0\)
\(\Leftrightarrow(\dfrac{5}{3}+\sqrt{x+3})\sqrt{x-3}=0\)
\(\Leftrightarrow\sqrt{x-3}=0\) (vì \(\dfrac{5}{3}+\sqrt{x+3}>0\))
\(\Leftrightarrow x-3=0\Leftrightarrow x=3\left(nhận\right)\)
Đúng 0
Bình luận (0)
Bài 1: Tìm x
a/\(\sqrt{1-4x+4x^2}\)+5=x-2
b/\(3\sqrt{12+4x}\)+\(\dfrac{4}{7}\sqrt{147+49x}\)=\(\dfrac{3}{2}\sqrt{48+16x}\)+4
`a)sqrt{1-4x+4x^2}+5=x-2`
`<=>\sqrt{(2x-1)^2}=x-2-5`
`<=>|2x-1|=x-7(x>=7)`
`<=>[(2x-1=x-7),(2x-1=7-x):}`
`<=>[(x=-6(ktm)),(3x=8):}`
`<=>x=8/3(ktm)`
Vậy PTVN
`b)3sqrt{12+4x}+4/7sqrt{147+49x}=3/2sqrt{48+16x}+4(x>=-3)`
`<=>6sqrt{x+3}+4sqrt{x+3}=6sqrt{x+3}+4`
`<=>4sqrt{x+3}=4`
`<=>sqrt{x+3}=1<=>x+3=1`
`<=>x=-2(tm)`
Vậy `S={-2}`
Đúng 1
Bình luận (0)
a) \(\sqrt{1-4x+4x^2}+5=x-2\Leftrightarrow\sqrt{\left(1-2x\right)^2}+5=x-2\Leftrightarrow\left|1-2x\right|=x-7\left(1\right)\)TH1: \(1-2x\ge0\Leftrightarrow x\le\dfrac{1}{2}\)
\(\left(1\right)\Leftrightarrow1-2x=x-7\Leftrightarrow3x=8\Leftrightarrow x=\dfrac{8}{3}\)(không thỏa đk)
TH2: \(1-2x< 0\Leftrightarrow x>\dfrac{1}{2}\)
\(\left(1\right)\Leftrightarrow2x-1=x-7\Leftrightarrow x=-6\)(không thỏa đk)
Vậy \(S=\varnothing\)
b) \(3\sqrt{12+4x}+\dfrac{4}{7}\sqrt{147+49x}=\dfrac{3}{2}\sqrt{48+16x}+4\Leftrightarrow6\sqrt{3+x}+4\sqrt{3+x}=6\sqrt{3+x}+4\Leftrightarrow4\sqrt{3+x}=4\Leftrightarrow\sqrt{3+x}=1\Leftrightarrow3+x=1\Leftrightarrow x=-2\)
Đúng 0
Bình luận (1)
a. \(\sqrt{1-4x+4x^2}+5=x-2\)
\(\Leftrightarrow\sqrt{\left(1-2x\right)^2}+5=x-2\)
\(\Leftrightarrow\left|1-2x\right|-x=-7\)
\(\Leftrightarrow\left[{}\begin{matrix}1-2x-x=-7\\2x-1-x=-7\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}-3x=-8\\x=-6\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{8}{3}\\x=-6\end{matrix}\right.\)
b. ĐKXĐ: \(x\ge-3\)
\(3\sqrt{12+4x}+\dfrac{4}{7}\sqrt{147+49x}=\dfrac{3}{2}\sqrt{48+16x}+4\)
\(\Leftrightarrow6\sqrt{3+x}+4\sqrt{3+x}-6\sqrt{3+x}=4\)
\(\Leftrightarrow4\sqrt{3+x}=4\) \(\Leftrightarrow\sqrt{3+x}=1\Leftrightarrow3+x=1\Leftrightarrow x=-2\) ( thỏa mãn đk )
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
2.tìm x
a)\(\sqrt{x^2-6x+9}\)
b)\(\sqrt{x^2-2x+1}\)
c)\(\sqrt{4x+12}-3\sqrt{x+3}+7\sqrt{9x+27}=20\)
d)\(\sqrt{4x+20}+3\sqrt{\dfrac{x-5}{9}}-\dfrac{1}{3}\sqrt{9x-45}=6\)
a) \(\sqrt{x^2-6x+9}\)
\(=\sqrt{\left(x^2-2.x.3+3^2\right)}\)
\(=\sqrt{\left(x-3\right)^2}\) ≥0,∀x
⇒x∈\(R\)
b) \(\sqrt{x^2-2x+1}\)
\(=\sqrt{\left(x^2-2.x.1+1^2\right)}\)
\(=\sqrt{\left(x-1\right)^2}\) ≥0,∀x
⇒x∈\(R\)
Đúng 0
Bình luận (0)
a) 2sqrt(25(x - 3)) - 1/2 * sqrt(4x - 12) + 1/7 * sqrt(49(x - 3)) = 20 b) sqrt(x ^ 2 - 6x + 9) = 2
Giải các phương trình sau:
a) \(\sqrt {11{x^2} - 14x - 12} = \sqrt {3{x^2} + 4x - 7} \)
b) \(\sqrt {{x^2} + x - 42} = \sqrt {2x - 30} \)
c) \(2\sqrt {{x^2} - x - 1} = \sqrt {{x^2} + 2x + 5} \)
d) \(3\sqrt {{x^2} + x - 1} - \sqrt {7{x^2} + 2x - 5} = 0\)
a) \(\sqrt {11{x^2} - 14x - 12} = \sqrt {3{x^2} + 4x - 7} \)
\(\begin{array}{l} \Rightarrow 11{x^2} - 14x - 12 = 3{x^2} + 4x - 7\\ \Rightarrow 8{x^2} - 18x - 5 = 0\end{array}\)
\( \Rightarrow x = - \frac{1}{4}\) và \(x = \frac{5}{2}\)
Thay nghiệm vừa tìm được vào phương trình \(\sqrt {11{x^2} - 14x - 12} = \sqrt {3{x^2} + 4x - 7} \) ta thấy chỉ có nghiệm \(x = \frac{5}{2}\) thảo mãn phương trình
Vậy nhiệm của phương trình đã cho là \(x = \frac{5}{2}\)
b) \(\sqrt {{x^2} + x - 42} = \sqrt {2x - 30} \)
\(\begin{array}{l} \Rightarrow {x^2} + x - 42 = 2x - 3\\ \Rightarrow {x^2} - x - 12 = 0\end{array}\)
\( \Rightarrow x = - 3\) và \(x = 4\)
Thay vào phương trình \(\sqrt {{x^2} + x - 42} = \sqrt {2x - 30} \) ta thấy không có nghiệm nào thỏa mãn
Vậy phương trình đã cho vô nghiệm
c) \(2\sqrt {{x^2} - x - 1} = \sqrt {{x^2} + 2x + 5} \)
\(\begin{array}{l} \Rightarrow 4.\left( {{x^2} - x - 1} \right) = {x^2} + 2x + 5\\ \Rightarrow 3{x^2} - 6x - 9 = 0\end{array}\)
\( \Rightarrow x = - 1\) và \(x = 3\)
Thay hai nghiệm trên vào phương trình \(2\sqrt {{x^2} - x - 1} = \sqrt {{x^2} + 2x + 5} \) ta thấy cả hai nghiệm đếu thỏa mãn phương trình
Vậy nghiệm của phương trình \(2\sqrt {{x^2} - x - 1} = \sqrt {{x^2} + 2x + 5} \) là \(x = - 1\) và \(x = 3\)
d) \(3\sqrt {{x^2} + x - 1} - \sqrt {7{x^2} + 2x - 5} = 0\)
\(\begin{array}{l} \Rightarrow 3\sqrt {{x^2} + x - 1} = \sqrt {7{x^2} + 2x - 5} \\ \Rightarrow 9.\left( {{x^2} + x - 1} \right) = 7{x^2} + 2x - 5\\ \Rightarrow 2{x^2} + 7x - 4 = 0\end{array}\)
\( \Rightarrow x = - 4\) và \(x = \frac{1}{2}\)
Thay hai nghiệm trên vào phương trình \(3\sqrt {{x^2} + x - 1} - \sqrt {7{x^2} + 2x - 5} = 0\) ta thấy chỉ có nghiệm \(x = - 4\) thỏa mãn phương trình
Vậy nghiệm của phương trình trên là \(x = - 4\)
Đúng 0
Bình luận (0)
2: Giải phương trình a) 2sqrt(25(x - 3)) - 1/2 * sqrt(4x - 12) + 1/7 * sqrt(49(x - 3)) = 20 b) sqrt(x ^ 2 - 6x + 9) = 2
a: \(\Leftrightarrow2\cdot5\sqrt{x-3}-\dfrac{1}{2}\cdot2\sqrt{x-3}+\dfrac{1}{7}\cdot7\sqrt{x-3}=20\)
=>\(10\cdot\sqrt{x-3}=20\)
=>\(\sqrt{x-3}=2\)
=>x-3=4
=>x=7
b: =>|x-3|=2
=>x-3=2 hoặc x-3=-2
=>x=5 hoặcx=1
Đúng 1
Bình luận (0)
\(25\sqrt{\dfrac{x-3}{25}}-7\sqrt{\dfrac{4x-12}{9}}-7\sqrt{x^2-9}+18\sqrt{\dfrac{9x^2-81}{81}}=0\)
Giải phương trình.
giúp e với ạaa :< gấp aa :((
\(25\sqrt{\dfrac{x-3}{25}}-7\sqrt{\dfrac{4x-12}{9}}-7\sqrt{x^2-9}+18\sqrt{\dfrac{9x^2-81}{81}}=0\left(x\ge3\right)\)
\(=25\sqrt{\dfrac{1}{25}.\left(x-3\right)}-7\sqrt{\dfrac{4}{9}.\left(x-3\right)}-7\sqrt{x^2-9}+18\sqrt{\dfrac{1}{9}.\left(x^2-9\right)}=0\)
\(=5\sqrt{x-3}-\dfrac{14}{3}\sqrt{x-3}-7\sqrt{x^2-9}+6\sqrt{x^2-9}=0\)
\(\Rightarrow\dfrac{1}{3}\sqrt{x-3}-\sqrt{\left(x-3\right)\left(x+3\right)}=0\Rightarrow\sqrt{x-3}-3\sqrt{\left(x-3\right)\left(x+3\right)}=0\)
\(\Rightarrow\sqrt{x-3}\left(1-3\sqrt{x+3}\right)=0\Rightarrow\left[{}\begin{matrix}\sqrt{x-3}=0\\1=3\sqrt{x+3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{26}{9}\left(l\right)\end{matrix}\right.\)
Đúng 2
Bình luận (1)
xét tính đồng biến nghịch biến
a) \(y=\sqrt{x^2-4x-3}\)
b) \(y=\sqrt{x^3-4x^2}\)
c) \(y=\left(2x+3\right)^{12}\left(6-5x\right)^9\left(x-7\right)^5\)
d) \(y=\sqrt{2x^3-3x^2}\)