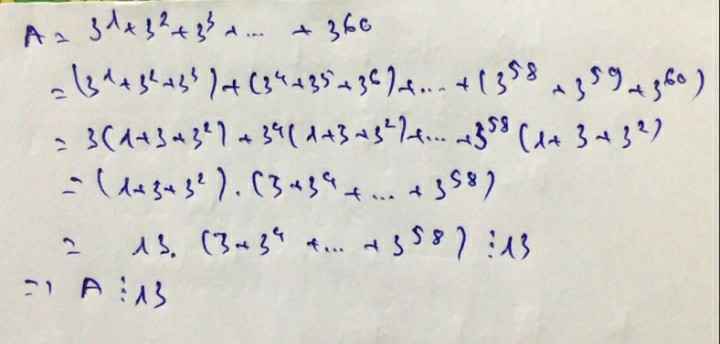chứng tỏ a+3^1+3^2+3^3+...+3^60 chia hết chi 13
PT
Những câu hỏi liên quan
Cho A=3^1+3^2+3^3+3^4+....+3^2015+3^2016.Chứng tỏ rằng A chia hết chi 4 và 13.
\(A=3+3^2+...+3^{2016}\)
\(A=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{2015}+3^{2016}\right)\)
\(A=3\cdot\left(1+3\right)+3^3\cdot\left(1+3\right)+...+3^{2015}\cdot\left(1+3\right)\)
\(A=4\cdot\left(3+3^3+...+3^{2015}\right)\)
Vậy A chia hết cho 4
_____________
\(A=3+3^2+3^3+...+3^{2016}\)
\(A=\left(3+3^2+3^3\right)+...+\left(3^{2014}+3^{2015}+3^{2016}\right)\)
\(A=3\cdot\left(1+3+9\right)+3^4\cdot\left(1+3+9\right)+...+3^{2014}\cdot\left(1+3+9\right)\)
\(A=13\cdot\left(3+3^4+...+3^{2014}\right)\)
Vậy A chia hết cho 13
Đúng 1
Bình luận (0)
a)A=2+2^2+2^3+2^4+...+2^60 chứng tỏ A chia hết cho 3, 7 ,15
b)B=3+3^2+3^3+3^4+...+3^1991 chứng tỏ B chia hết cho 13 và 41
B,Chứng tỏ rằng:A=3^1+3^2+3^3+.....+3^60 chia hết cho 13
a,Chứng minh rằng A là một lũy thừa của 2
A=4+2^2+2^3+2^4+......+2^20
b,Chứng tỏ A=3^1+3^2+3^3+.....+3^60 chia hết cho 13
b: \(A=3\left(1+3+3^2\right)+...+3^{58}\left(1+3+3^2\right)\)
\(=13\left(3+...+3^{58}\right)⋮13\)
Đúng 4
Bình luận (0)
\(a,\Leftrightarrow2A=8+2^3+2^4+...+2^{21}\\ \Leftrightarrow2A-A=8+2^3+2^4+...+2^{21}-4-2^2-2^3-...-2^{20}\\ \Leftrightarrow A=2^{21}+8-4-2^2=2^{21}\left(đpcm\right)\\ b,A=\left(3+3^2+3^3\right)+\left(3^4+3^5+3^6\right)+...+\left(3^{58}+3^{59}+3^{60}\right)\\ A=3\left(1+3+3^2\right)+3^4\left(1+3+3^2\right)+...+3^{58}\left(1+3+3^2\right)\\ A=\left(1+3+3^2\right)\left(3+3^4+...+3^{58}\right)\\ A=13\left(3+3^4+...+3^{58}\right)⋮13\)
Đúng 1
Bình luận (0)
a,Chứng minh rằng A là một lũy thừa của 2
A=4+2^2+2^3+2^4+......+2^20
b,Chứng tỏ A=3^1+3^2+3^3+.....+3^60 chia hết cho 13
Đúng 0
Bình luận (0)
Chứng tỏ :
a) C = 1 + 5 + 5^2 + 5^3 + ... + 5^403 + 5^404 chia hết cho 31.
b) E = 3 + 3^2 + 3^3 + ... + 3^60 vừa chia hết cho 4 , vừa chia hết cho 13.
Chứng tỏ : A = 31 + 32 + 33 +...+360 chia hết cho 13
Bạn tham khảo ở đây: Câu hỏi của Lê Diệu Chinh - Toán lớp 6 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
chứng tỏ : A = 31 + 32 + 33 + ... + 360 chia hết cho 13
A=3+3^2+3^3+....+3^60
A=(3+3^2+3^3+3^4)+(3^5+3^6+3^7+3^8)+....+(3^57+3^58+3^59+3^60)
A=39+3^4(3+3^2+3^3+3^4)+...+3^56.(3+3^2+3^3+3^4)
A=39+3^4.39+...+3^56.39
A=39.(1+3^4+...+3^56)\(⋮13\)
=>\(A⋮13\)
Đúng 0
Bình luận (0)
Cho B=3+3^ 2 +3^ 3 +***+3^ 60 Chứng tỏ rằng B chia hết cho 13 .
Số số hạng của B:
60 - 1 + 1 = 60 (số)
Do 60 chia hết cho 3 nên ta nhóm các số hạng của B thành nhóm 3 số hạng như sau:
B = 3 + 3² + 3³ + ... + 3⁶⁰
= (3 + 3² + 3³) + (3⁴ + 3⁵ + 3⁶) + ... + (3⁵⁸ + 3⁵⁹ + 3⁶⁰)
= 3.(1 + 3 + 3²) + 3⁴.(1 + 3 + 3²) + ... + 3⁵⁸.(1 + 3 + 3²)
= 3.13 + 3⁴.13 + ... + 3⁵⁸.13
= 13.(3 + 3⁴ + ... + 3⁵⁸) ⋮ 13
Vậy B ⋮ 13
Đúng 2
Bình luận (0)
giải bài toán sau a) cho M = 2 mũ 1+ 2 mũ 2+ 2 mũ 3+ 2 mũ 4+....................+2 mũ 20.chứng tỏ rằng M chia hết cho5
b) tìm số dư khi chia B cho 13,với B = 3 mũ 0+3 mũ 1+ 3 mũ 2+3 mũ 3+................+3 mũ 60
c) cho abc-deg chia hết cho 7.chứng tỏ rằng abcdeg chia hết cho 7
con khong biet