bài 3 mn ơi


mn ơi giúp mik bài 3 nhé cảm ơn mn
3:
a: A={2;4;...;98}
A có (98-2):2+1=49 phần tử
B={2;3;4;5;...;50}
B có 50-2+1=49 phần tử
b: A giao B={2;4}
c: Đó ko là tập con của A hay B vì A và B đều ko chứa số 0
Mn ơi mik cần gấp chỉ mik bài 2 bài 3 vs ạ mik cảm ơn mn trc ạ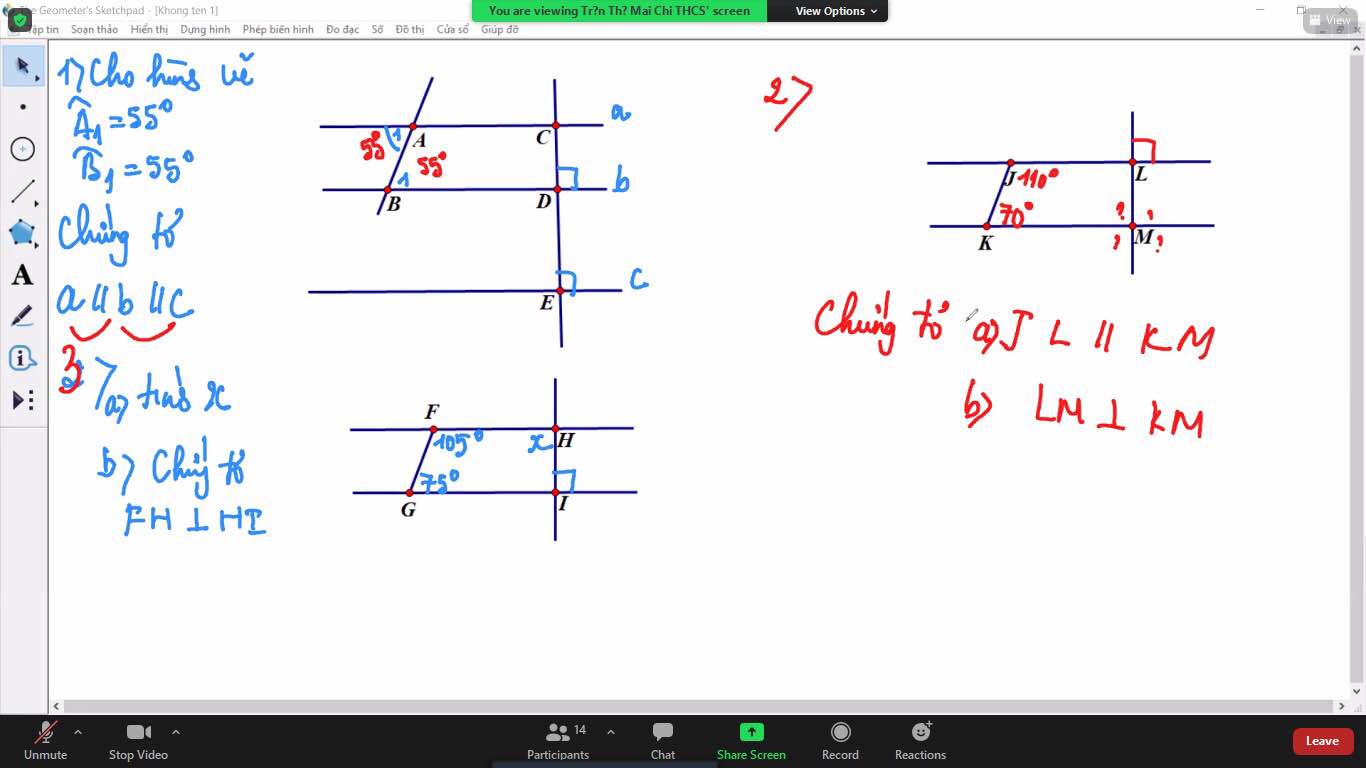
Mn ơi, giúp mik bài 3 đc k ạ mik cảm ơn mn trc ạ
Do \(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{b}{a}=\dfrac{d}{c}\)
\(\Rightarrow1-\dfrac{b}{a}=1-\dfrac{d}{c}\Rightarrow\dfrac{a-b}{a}=\dfrac{c-d}{c}\) (đpcm)
Mn ơi giải giúp mik bài 3 vs, cảm ơn mn nhiềuuuu nha 😷😊
a: =3/2-2/3:(4/18+3/18)
=3/2-2/3:7/18
=3/2-2/3*18/7
=3/2-12/7
=-3/14
b: =(5/8-1/5)*2-1/4
=5/4-2/5-1/4
=1-2/5=3/5
c: =(3+5/6-1/2):55/12
=10/3*12/55
=8/11
Giúp em 3 bài này với mn ơi 
1.
Với \(n=0;1\) không thỏa mãn
Với \(n>1\)
\(A=\left(n^2+n\right)^2+n^2+3n+7>\left(n^2+n\right)^2\)
\(A=\left(n^2+n+2\right)^2-\left[3\left(n^2-1\right)+n\right]< \left(n^2+n+2\right)^2\)
\(\Rightarrow\left(n^2+n\right)^2< A< \left(n^2+n+2\right)^2\)
\(\Rightarrow A=\left(n^2+n+1\right)^2\)
\(\Rightarrow n^4+2n^3+2n^2+3n+7=\left(n^2+n+1\right)^2\)
\(\Rightarrow n^2-n-6=0\Rightarrow\left[{}\begin{matrix}n=-2\left(loại\right)\\n=3\end{matrix}\right.\)
3.
TH1:
\(x>y\Rightarrow x^2y^2+x-y>x^2y^2\)
Mặt khác x; y nguyên dương \(\Rightarrow y\ge1\Rightarrow xy-\left(x-y\right)=x\left(y-1\right)+y>0\Rightarrow xy>x-y\)
\(\Rightarrow2xy+1>x-y\Rightarrow x^2y^2+x-y< x^2y^2+2xy+1\)
\(\Rightarrow x^2y^2< x^2y^2+x-y< \left(xy+1\right)^2\)
\(\Rightarrow x^2y^2+x-y\) nằm giữa 2 SCP liên tiếp nên ko thể là SCP (trái giả thiết) \(\Rightarrow\) loại
TH2: \(x< y\Rightarrow x^2y^2+x-y< x^2y^2\)
\(x-y-\left(-2xy+1\right)=\left(x-1\right)+y\left(2x-1\right)>0\Rightarrow x-y>-2xy+1\)
\(\Rightarrow x^2y^2+x-y>x^2y^2-2xy+1=\left(xy-1\right)^2\)
\(\Rightarrow\left(xy-1\right)^2< x^2y^2+x-y< x^2y^2\)
\(\Rightarrow x^2y^2+x-y\) nằm giữa 2 SCP liên tiếp \(\Rightarrow\) ko thể là SCP => trái giả thiết => loại
Vậy \(x=y\)
2.
\(C=n^4-2n^3+3n^2-6n+8\)
\(C=\left(n^2-n\right)^2+2n^2-6n+8=\left(n^2-n\right)^2+2\left(n-\dfrac{3}{2}\right)^2+\dfrac{7}{2}>\left(n^2-n\right)^2\)
\(C=\left(n^2-n+3\right)^2-\left(4n^2+1\right)< \left(n^2-n+3\right)^2\)
\(\Rightarrow\left(n^2-n\right)^2< C< \left(n^2-n+3\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}C=\left(n^2-n+1\right)^2\\C=\left(n^2-n+2\right)^2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}4n-7=0\left(vn\right)\\2n^2+2n-4=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}n=1\\n=-2\end{matrix}\right.\)
Mn ơi giúp em bài 3 với ạ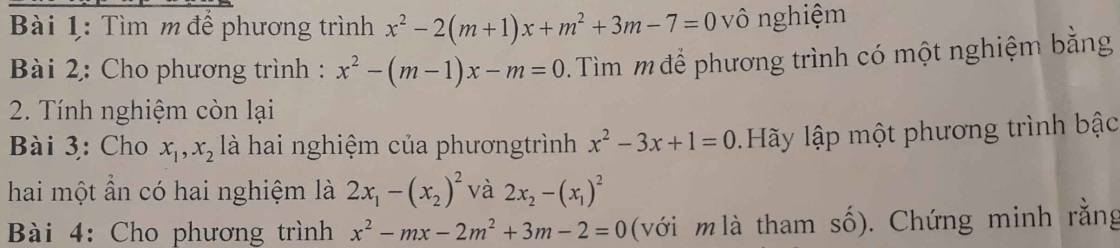
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=1\end{matrix}\right.\)
Gọi \(x_3;x_4\) là các nghiệm của pt cần tìm, ta có:
\(\left\{{}\begin{matrix}x_3+x_4=2x_1-x_2^2+2x_2-x_1^2\\x_3x_4=\left(2x_1-x_2^2\right)\left(2x_2-x_1^2\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_3+x_4=2\left(x_1+x_2\right)-\left(x_1+x_2\right)^2+2x_1x_2\\x_3x_4=4x_1x_2-2x_1^3-2x_2^3+\left(x_1x_2\right)^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_3+x_4=2\left(x_1+x_2\right)-\left(x_1+x_2\right)^2+2x_1x_2\\x_3x_4=4x_1x_2-2\left[\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\right]+\left(x_1x_2\right)^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_3+x_4=2.3-3^2+2.1=-1\\x_3x_4=4.1-2\left(3^3-3.1.3\right)+1^2=-31\end{matrix}\right.\)
Theo định lý Viet đảo, pt cần tìm có dạng:
\(x^2+x-31=0\)
Giúp mình bài 3 với mn ơi mình cảm ơn 
Bài 3:
\(n_{Al}=\dfrac{5,4}{27}=0,2\left(mol\right)\\ a.2Al+6HCl\rightarrow2AlCl_3+3H_2\\ 0,2..........0,6...........0,2..........0,3\left(mol\right)\\ V_{H_2\left(đktc\right)}=0,3.22,4=6,72\left(l\right)\\ b.m_{AlCl_3}=133,5.0,2=26,7\left(g\right)\\ c.V_{ddHCl}=\dfrac{0,6}{0,8}=0,75\left(l\right)\)
Cứu em mn ơi tối nộp rùi Bài 3 nha
