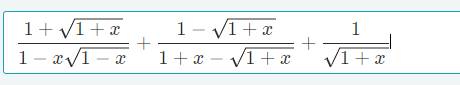
a) rút gọn biểu thức A
b) chứng minh A luôn dương với mọi giá trị của a
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho biểu thức M = (2x-3)^2-x(3-x)+5x-4x^2+17
a)rút gọn biểu thức M
b)chứng minh giá trị biểu thức M luôn giá trị dương với mọi x
`#3107.\text {DN}`
a)
\((2x-3)^2-x(3-x)+5x-4x^2+17\)
`= 4x^2 - 12x + 9 - 3x + x^2 + 5x - 4x^2 + 17`
`= x^2 - 10x + 26`
b)
`M = x^2 - 10x + 26`
`= [(x)^2 - 2*x*5 + 5^2] + 1`
`= (x - 5)^2 + 1`
Vì `(x - 5)^2 \ge 0` `AA` `x => (x - 5)^2 + 1 \ge 1` `AA` `x`
Vậy, giá trị biểu thức M luôn có giá trị dương với mọi x.
Cho biểu thức :
A=(x2 + 2)2 _ (x - 2).(x + 2).(x2 + 4)
a. Rút gọn biểu thức A
b. Tính giá trị của A khi x = -2 , x=0 , x=2
c Chứng minh rằng A luôn có giá trị dương với mọi x
Cho biểu thức: B = (2x+5)2 – (3-x)(3+x) + 14
a) Thu gọn biểu thức B
b) Chứng minh giá trị của biểu thức B luôn luôn dương với mọi giá trị của biến x.
Cho biểu thức: B = (2x+5)2 – (3-x)(3+x) + 14
a) Thu gọn biểu thức B
b) Chứng minh giá trị của biểu thức B luôn luôn dương với mọi giá trị của biến x.
\(a,B=4x^2+20x+25-9+x^2+14=5x^2+20x+30\\ b,B=5\left(x^2+4x+4\right)+10\\ B=5\left(x+2\right)^2+10\ge10>0,\forall x\)
Do đó B luôn dương với mọi x
Cho A = ( 2x + 1 )2 - ( x + 2 ) ( x - 2 ) - 2x ( x + 1 )
a, Rút gọn A
b, Tìm giá trị x để giá trị của biểu thức A = 4
c, Chứng minh A có giá trị dương với mọi x
a) \(A=\left(2x+1\right)^2-\left(x+2\right)\left(x-2\right)-2x\left(x+1\right)\)
\(A=4x^2+4x+1-x^2+4-2x^2-2x\)
\(A=x^2+2x+5\)
b) Để A = 4
=> \(x^2+2x+5=4\)
\(\Leftrightarrow x^2+2x+1=0\)
\(\Leftrightarrow\left(x+1\right)^2=0\)
\(\Leftrightarrow x+1=0\Leftrightarrow x=-1\)
c) Ta có A = x2 + 2x + 5
A = ( x + 1 )2 + 4
=> \(A\ge4>0\left(đpcm\right)\)
a,\(A=\left(2x+1\right)^2-\left(x+2\right)\left(x-2\right)-2x\left(x+1\right)\)
\(=4x^2+4x+1-x^2+4-2x^2-2x\)
\(=x^2+2x+5\)
b,\(A=x^2+2x+5=4\)
\(\Rightarrow x^2+2x+5-4=0\)
\(x^2+2x+1=0\)
\(\left(x+1\right)^2=0\)
\(x+1=0\)
\(x=-1\)
c, Ta có: \(A=x^2+2x+5=\left(x^2+2x+1\right)+4=\left(x+1\right)^2+4\ge4>0\)
Hay: A > 0 => đpcm
=.= hok tốt!!
Chứng minh các biểu thức sau luôn luôn có giá trị dương với mọi giá trị của biến:
a) A= x^2 + x + 1
b) B= 2x^2 + 2x +1
a)\(A=x^2+x+1=\left(x^2+x+\dfrac{1}{4}\right)+\dfrac{3}{4}=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\)
b) \(B=2x^2+2x+1=2\left(x^2+x+\dfrac{1}{4}\right)+\dfrac{1}{2}=2\left(x+\dfrac{1}{2}\right)^2+\dfrac{1}{2}\ge\dfrac{1}{2}>0\)
cho biểu thức A=\(\dfrac{1}{x-2}+\dfrac{1}{x+2}+\dfrac{x^2+1}{x^2-4}\) (với x ≠+-2)
a) rút gọn A
b)chứng tỏ rằng với mọi x thõa mãn -2<x<2, x≠-1 biểu thức A luôn có giá trị âm
a) \(A= \dfrac{1}{x-2}+\dfrac{1}{x+2}+\dfrac{x^2+1}{x^2-4} \\ =\dfrac{1}{x-2}+\dfrac{1}{x-2}+\dfrac{x^2+1}{(x-2)(x+2)} \\= \dfrac{x+2+x-2+x^2+1}{(x-2)(x+2)} \\=\dfrac{x^2+2x+1}{x^2-4} \\ =\dfrac{(x+1)^2}{(x-2)(x+2)}\)
b) Với mọi \(x\) thỏa mãn \(-2<x<2\) và \(x \ne -1\) thì \(x-2\) đều có giá trị âm, mà \(\begin{cases}(x+1)^2≥0\\x+2>0\\\end{cases}\) \( \Rightarrow\) Biểu thức A luôn có giá trị âm.
Cho phân thức: A=(3-6x)/(2x^3-x^2+2x-1) a) Rút gọn phân thức. b) Tính giá trị của phân thức tại x=3. c) Chứng minh A luôn âm với mọi giá trị của x khác 1/2.
a: \(A=\dfrac{3\left(1-2x\right)}{2x\left(x^2+1\right)-\left(x^2+1\right)}\)
\(=\dfrac{-3\left(2x-1\right)}{\left(x^2+1\right)\left(2x-1\right)}=\dfrac{-3}{x^2+1}\)
b: Khi x=3 thì \(A=\dfrac{-3}{3^2+1}=-\dfrac{3}{10}\)
c: x^2+1>=0
=>3/x^2+1>=0
=>-3/x^2+1<=0
=>A<=0(ĐPCM)
Chứng minh các biểu thức sau luôn dương với mọi giá trị của biến :
a, F=4x^2 - 12 + 11
\(Sửa:F=4x^2-12x+11=\left(4x^2-12x+9\right)+2=\left(2x-3\right)^2+2\ge2>0\left(đpcm\right)\)
Chú ý rằng nếu c > 0 thì a + b 2 + c và a + b 2 + c đều dương với mọi a, b. Áp dụng điều này chứng minh rằng:
Với mọi giá trị của x khác ± 1, biểu thức:
x + 2 x - 1 x 3 2 x + 2 + 1 - 8 x + 7 2 x 2 - 2 luôn luôn có giá trị dương.
Điều kiện x ≠ 1 và x ≠ - 1
Ta có:

Biểu thức dương khi x 2 + 2 x + 3 > 0
Ta có: x 2 + 2 x + 3 = x 2 + 2 x + 1 + 2 = x + 1 2 + 2 > 0 với mọi giá trị của x.
Vậy giá trị của biểu thức dương với mọi giá trị x ≠ 1 và x ≠ - 1