Cho hình vẽ: AB = AC; BD = CD
a, tam giác ABD bằng tam giác ACD
b, AD cắt BC tại I .Chứng minh tam giac ABI = tam giác ACI
c, Chứng minh AD vuông góc BC tại I ,I là trung điểm của BC
EM DANG CAN GAP A!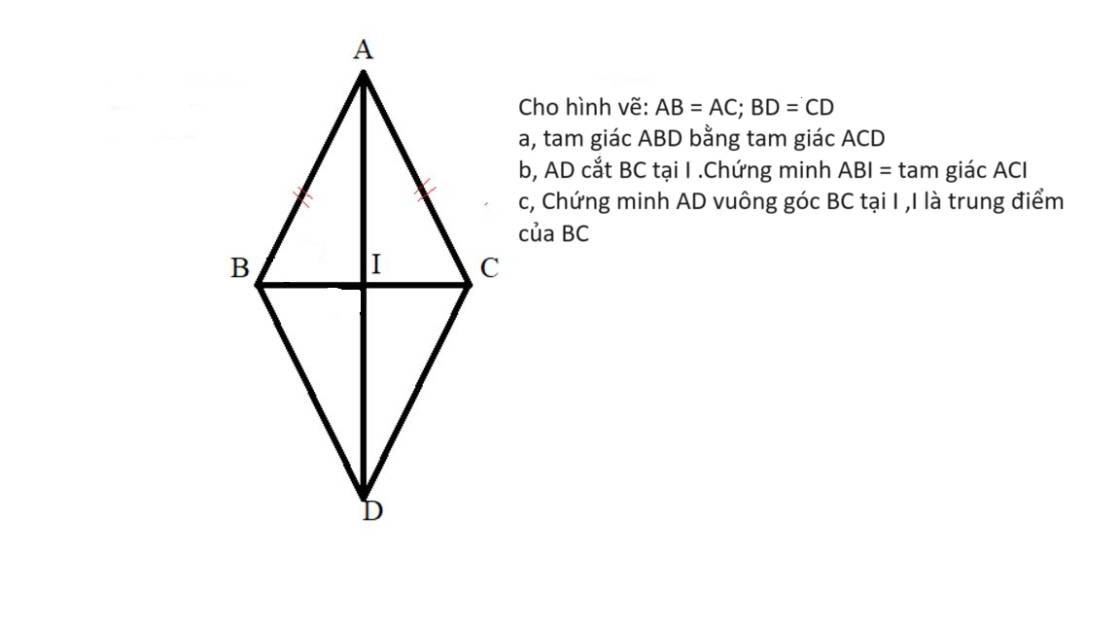
2) Cho hình vẽ bên: (hình này là hình bình hành có AB=CE; AC=BE)
CM AB//CE và AC//BE
Xét tứ giác ABEC có
AB//EC
AC=BE
=>ABEC là hình bình hành
=>AB//CE và AC//BE
Cho tam giác \(ABC\) vuông tại \(A\) (\(AB < AC\). Gọi \(D\) là trung điểm của \(BC\). Vẽ \(DE\) // \(AB\), vẽ \(DF\) // \(AC\) \((E \in AC\); \(F \in AB)\). Chứng minh rằng:
a) Tứ giác \(AEDF\) là hình chữ nhật
b) Tứ giác \(BFED\) là hình bình hành
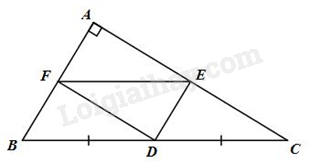
a) Ta có:
\(\Delta ABC\) vuông tại \(A\) nên \(\widehat {{\rm{BAC}}} = 90^\circ \) và \(AB \bot AC\)
Mà \(DE\) // \(AB\) ; \(DF\) // \(AC\)
Suy ra \(DE \bot AC;\;DF \bot AB\)
Suy ra \(\widehat {DEA} = \widehat {DFA} = 90^\circ \)
Tứ giác \(AEDF\) có \(\widehat {BAC} = \widehat {DEA} = \widehat {DFA} = 90^\circ \) nên là hình chữ nhật
b) Vì \(AEDF\) là hình chữ nhật (cmt)
Suy ra \(AE = DF\); \(AF = DE\); \(AF\) // \(DE\); \(AE\) // \(DF\)
Vì \(DE \bot AC;\;DF \bot AB\) (cmt)
Suy ra \(\widehat {DEC} = \widehat {BFD} = 90^\circ \)
Xét \(\Delta BFD\) và \(\Delta DEC\) ta có:
\(\widehat {{\rm{BFD}}} = \widehat {{\rm{DEC}}} = 90^\circ \) (cmt)
\(BD = DC\) (gt)
\(\widehat {{\rm{FBD}}} = \widehat {{\rm{EDC}}}\) (do \(DE\) // \(BF\) )
Suy ra \(\Delta BFD = \Delta DEC\) (ch – gn)
Suy ra \(BF = DE\); \(DF = EC\) (hai cạnh tương tứng)
Xét tứ giác \(BFED\) ta có:
\(BF\) // \(DE\) (do \(AB\) // \(DE\))
\(BF = DE\) (cmt)
Suy ra \(BFED\) là hình bình hành
Cho tam giác ABC vuông tại A có AB/AC=3/4 AC =15cm tính AB. AC(VẼ HÌNH HỘ)
sai đề, sửa: BC=15cm
\(\frac{AB}{AC}=\frac{3}{4}\Rightarrow AB=\frac{3AC}{4}\)
Áp dụng định lý pytago vào tam giác vuông ABC. ta có:
AB2+AC2=BC2
=> \(\left(\frac{3}{4}AC\right)^2+AC^2=15^2\)
\(AC^2.\left(\frac{9}{16}+1\right)=15^2\Rightarrow AC^2.\left(\frac{5}{4}\right)^2=15^2\)
\(\Rightarrow AC^2=15^2.\left(\frac{4}{5}\right)^2=12^2\Rightarrow AC=12\)
\(AB=\frac{3.AC}{4}=9\)
-bài này vẽ hình làm cảnh à :V
Vẽ hình sau: Cho ΔABC, góc A < 90o. Trên nửa mặt phẳng bờ là AB không chứa điểm C, vẽ tia Ax ⊥ AB và lấy trên Ax điểm D sao cho AD = AB. Trên nửa mặt phẳng bờ AC không chứa B, vẽ tia Ay ⊥ AC và lấy điểm E sao cho AE = AC. Chứng minh:
a) BE = CD.
b) BE ⊥ CD
c) Lấy M; N là trung điểm BE; DC. Chứng minh AM = AN.
a:\(\widehat{DAC}=\widehat{DAB}+\widehat{BAC}=90^0+\widehat{BAC}\)
\(\widehat{BAE}=\widehat{BAC}+\widehat{CAE}=90^0+\widehat{BAC}\)
Do đó: \(\widehat{DAC}=\widehat{BAE}\)
Xét ΔDACvà ΔBAE có
AD=AB
\(\widehat{DAC}=\widehat{BAE}\)
AC=AE
Do đó: ΔDAC=ΔBAE
=>DC=BE
b: ΔDAC=ΔBAE
=>\(\widehat{ADC}=\widehat{ABE};\widehat{ACD}=\widehat{AEB}\)
\(\widehat{CEB}+\widehat{ECD}\)
\(=\widehat{CEB}+\widehat{ECA}+\widehat{DCA}\)
\(=\widehat{ECA}+\widehat{AEB}+\widehat{CEB}\)
\(=\widehat{ECA}+\widehat{AEC}=90^0\)
=>BE\(\perp\)CD
Cho tam giác ABC vuông tại A, AB < AC; AD là phân giác, Vẽ DE⊥AB tại E, DF⊥AC tại F.
a) Tứ giác AEDF là hình gì?
b) Qua D, vẽ đường thẳng m ⊥ BC, m cắt AC tại K. Chứng minh: DK = DB
Please cho mình cả hình nữa ạ. Help me pleaseeeee ![]()
a: Xét tứ giác AEDF có
\(\widehat{FAE}=\widehat{AFD}=\widehat{AED}=90^0\)
Do đó: AEDF là hình chữ nhật
mà AD là tia phân giác của \(\widehat{FAE}\)
nên AEDF là hình vuông
Cho tam giác ABC (AB < AC), vẽ E, F, G lần lượt là trung điểm AB, AC, BC.
a/ Chứng minh tứ giác BEFC là hình thang.
b/ Vẽ AH vuông góc BC (H thuộc BC). Chứng minh tứ giác EFGH là hình thang cân.
\(a,\left\{{}\begin{matrix}AE=EB\\AF=FC\end{matrix}\right.\Rightarrow EF\) là đtb tam giác ABC
\(\Rightarrow EF//BC\Rightarrow BEFC\) là hthang
\(b,EF//BC\Rightarrow EF//GH\Rightarrow EFGH\) là hthang
Có HF là trung tuyến ứng cạnh huyền tam giác AHC nên \(HF=\dfrac{1}{2}AC\)
Mà \(\left\{{}\begin{matrix}AE=EB\\BG=GC\end{matrix}\right.\Rightarrow EG\) là đtb tg ABC \(\Rightarrow EG=\dfrac{1}{2}AC\)
Do đó \(HF=EG\) nên EFGH là hthang cân
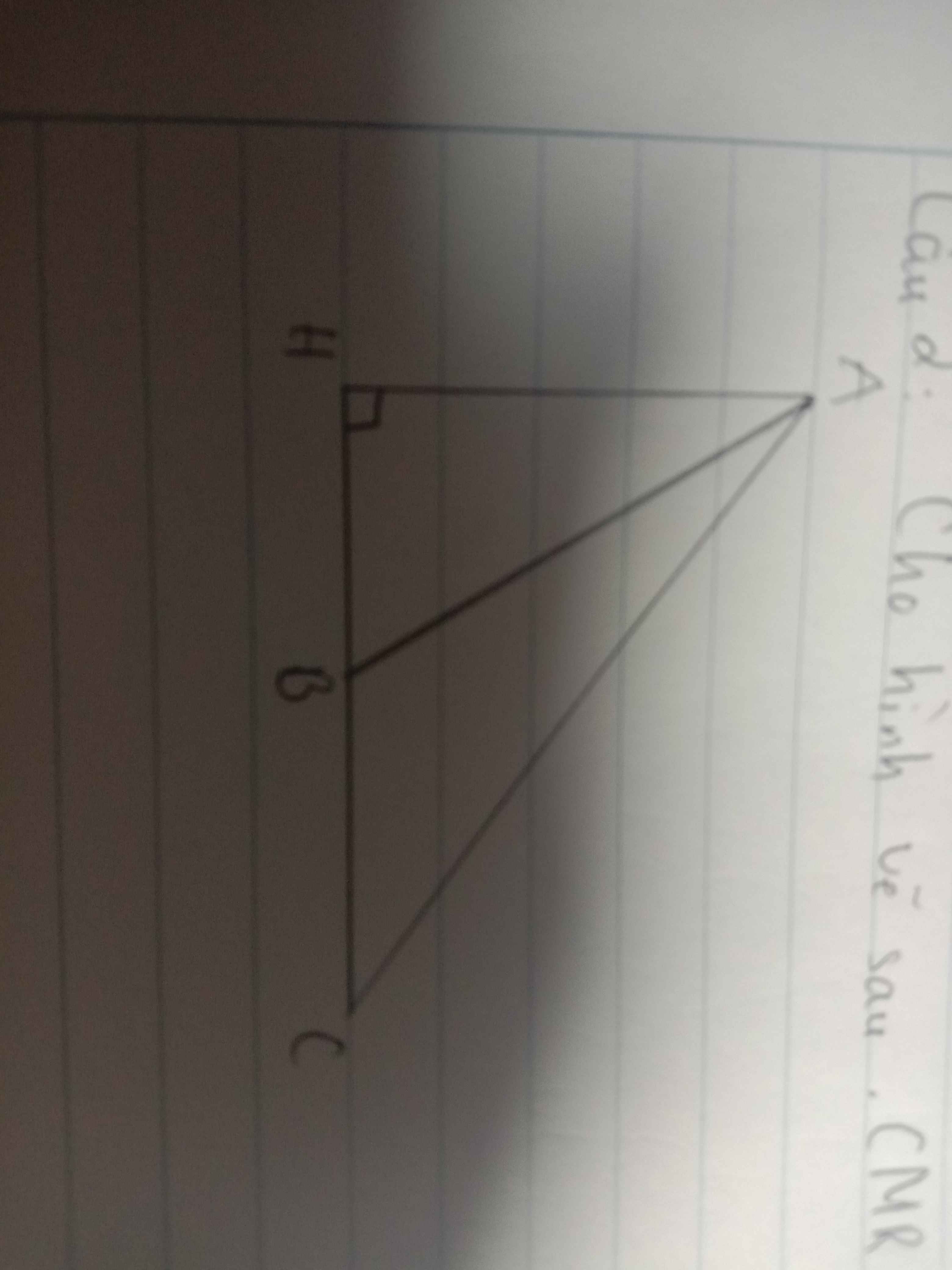 Cho hình vẽ sau. Chứng minh rằng AH<AB<AC
Cho hình vẽ sau. Chứng minh rằng AH<AB<AC
Hãy chọn câu sai. Cho hình vẽ với AB < AC:
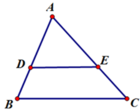
A. A D A B = A E A C => DE // BC
B. A D B D = A E E C => DE // BC
C. A B B D = A C E C ⇒ D E / / B C
D. A D D E = A E E D => DE // BC
Theo định lý đảo của định lý Ta-lét. Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Nên D sai.
Đáp án: D
vẽ hộ mình hình bài này nhé thanks mọi người nhiều : cho tam giác nhọn ABC có AB > AC , vẽ đường cao AH . vẽ M , N sao cho AB , AC lần lượt là trung trực của các đoạn thẳng HM , HN