Tìm max hoặc min:
A= ( 2x 2 + 3 ) -7
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
JM
Những câu hỏi liên quan
Tìm Min:
a, A= 4x^2 - 4x +10
b, B= 2x^2 + 6x
c, C= x^2 - x
tìm max hoặc min
A=-(x-7)2-888
B=8/3+ |2x-1|+|y-5|
C=(x+3)2+|2y-5|-232
D=21-|3x+5|-|y-1|-(8+z)
a: A=-(x-7)^2-888<=-888
Dấu = xảy ra khi x=7
b: \(B=\left|2x-1\right|+\left|y-5\right|+\dfrac{8}{3}>=\dfrac{8}{3}\)
Dấu = xảy ra khi x=1/2 và y=5
c: \(C=\left(x+3\right)^2+\left|2y-5\right|-232>=-232\)
Dấu = xảy ra khi x=-3 và y=5/2
Đúng 0
Bình luận (0)
Bài 1: Tìm MIN:
a. x^2-x+1
b. x^2+y^2-4x+y+5
c. x^2+2y^+2xy+2x+4y-10
a: Ta có: \(x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{4}\)
b: Ta có: \(x^2+y^2-4x+y+5\)
\(=\left(x^2-4x+4\right)+\left(y^2+y+\dfrac{1}{4}\right)+\dfrac{3}{4}\)
\(=\left(x-2\right)^2+\left(y+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x,y\)
Dấu '=' xảy ra khi x=2 và \(y=-\dfrac{1}{2}\)
Đúng 2
Bình luận (0)
Tìm max hoặc min của A= -2x^2-8x+1
B=3x^2+3x-1
C=7x-2x^2+3
D=-4xy+4x-y^2-5x^2+3
\(B=3x^2+3x-1\)
\(=3\left(x^2+x-\dfrac{1}{3}\right)\)
\(=3\left(x^2+x+\dfrac{1}{4}-\dfrac{7}{12}\right)\)
\(=3\left(x+\dfrac{1}{2}\right)^2-\dfrac{7}{4}>=-\dfrac{7}{4}\forall x\)
Dấu '=' xảy ra khi x+1/2=0
=>\(x=-\dfrac{1}{2}\)
\(C=-2x^2+7x+3\)
\(=-2\left(x^2-\dfrac{7}{2}x-\dfrac{3}{2}\right)\)
\(=-2\left(x^2-2\cdot x\cdot\dfrac{7}{4}+\dfrac{49}{16}-\dfrac{73}{16}\right)\)
\(=-2\left(x-\dfrac{7}{4}\right)^2+\dfrac{73}{8}< =\dfrac{73}{8}\forall x\)
Dấu '=' xảy ra khi x-7/4=0
=>x=7/4
Đúng 0
Bình luận (0)
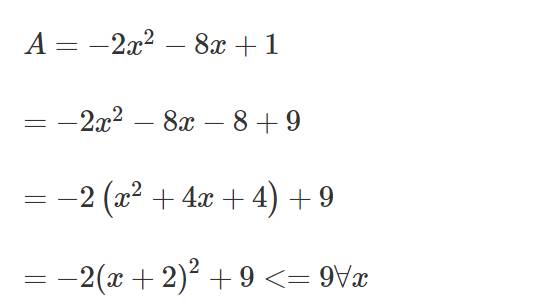
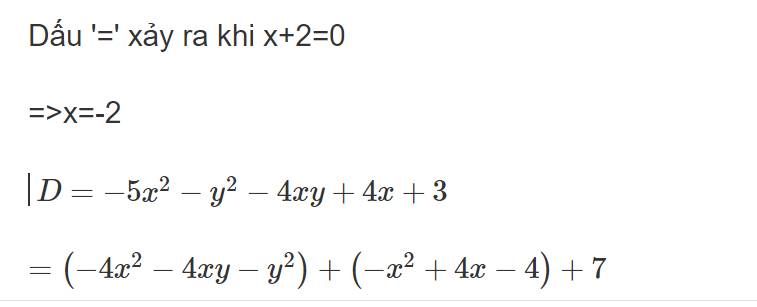
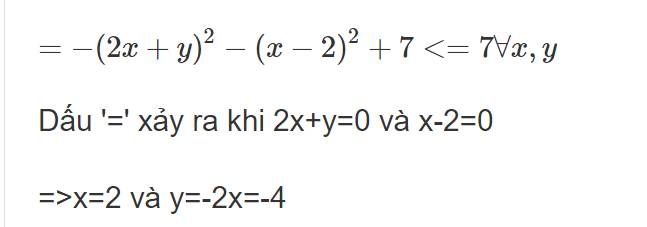
1/ 3x2 + 6x - 11
2/ \(\frac{3x^2+2x+7}{3x^2+2x+1}\)
Tìm Max hoặc Min
1/
\(A=3x^2+6x-11\)\(=3\left(x^2+2x-\frac{11}{3}\right)\)\(=3\left[\left(x^2+2x+1\right)-\frac{14}{3}\right]\)\(=3\left(x+1\right)^2-14\ge-14\)
VẬY \(minA=-14\)khi \(x=-1\)
2/
\(B=\frac{3x^2+2x+7}{3x^2+2x+1}=1+\frac{6}{3x^2+2x+1}\)
Biểu thức \(\frac{6}{3x^2+2x+1}\)đạt GTLN khi \(3x^2+2x+1\)nhỏ nhất
Mà \(3x^2+2x+1\ge1\)nên GTNN của \(3x^2+2x+1\)là \(1\)
Ta có : \(maxB=1+6=7\) khi \(x=0\)
TK mk nka !!!!!
Đúng 0
Bình luận (0)
\(3x^2+6x-11=3\left(x^2+2x+1\right)-14=3\left(x+1\right)^2-14\ge-14\) \(\Rightarrow Min=-14\Leftrightarrow x=-1\)\(B=\frac{3x^2+2x+7}{3x^2+2x+1}=1+\frac{6}{3x^2+2x+1}\)phân số đạt lớn nhất khi \(3x^2+2x+1\)giá trị nhỏ nhất nên \(3x^2+2x+1=3x^2+\frac{2.\sqrt{3}}{\sqrt{3}}x+\frac{1}{3}+\frac{4}{3}=\left(x\sqrt{3}+\frac{1}{\sqrt{3}}\right)^2+\frac{4}{3}\ge\frac{4}{3}\)
\(\Rightarrow B_{max}=1+\frac{6}{\frac{4}{3}}=\frac{11}{2}\Leftrightarrow x=-\frac{1}{3}\)
Đúng 0
Bình luận (0)
Ta có : 3x2 + 6x - 11
= 3x2 + 3.x.3 - 9 - 2
= (3x2 - 3)2
Mà (3x - 3)2 \(\le0\forall x\in R\)
Nên 3x2 + 6x - 11 min = 0 khi x = 1
Đúng 0
Bình luận (0)
tìm min hoặc max của 2x2+x
Bài 1 Tìm Min hoặc Max
a)2x^2+10x-1
b) 5x - x^2
c) 2x^2-8x-10
d)9x-3x^2
Bài 2 Phân Tích x^4-2x^3-2x^2-2x-3
Bài 1 Tìm Min hoặc Max
a)2x^2+10x-1
b) 5x - x^2
c) 2x^2-8x-10
d)9x-3x^2
Bài 2 Phân Tích x^4-2x^3-2x^2-2x-3
tìm min hoặc max của 2x2 +x
Bài này tìm được min thôi
Ta có: \(2x^2+x=2\left(x^2+\frac{1}{2}x+\frac{1}{16}\right)-\frac{1}{8}=2\left(x+\frac{1}{4}\right)^2-\frac{1}{8}\ge-\frac{1}{8}\left(\forall x\right)\)
Dấu "=" xảy ra khi: \(2\left(x+\frac{1}{4}\right)^2=0\Rightarrow x=-\frac{1}{4}\)
Vậy Min = -1/8 khi x = -1/4